Оптимизация подмножества массивов с помощью составных агрегатных функций

Question

Оптимизация подмножества массивов с помощью составных агрегатных функций

У меня есть массив P = [1, 5, 3, 6, 4, ...] размера N и в среднем A,

Я хочу найти наиболее эффективный способ максимизировать следующую 3D-функцию:

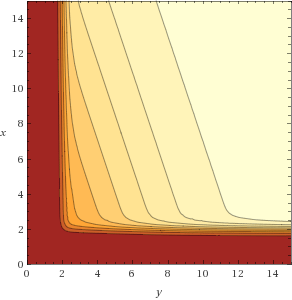
f(x, y) = 1 / ( (1+e^(-6(x-2))) * (1+e^(-6(y-2))) * (1+e^(-0.1x-0.3y+1.5)) )

где x = c(S) = Count(S) а также y = m(S) = Min(S[0]/A, S[1]/A, ..., S[n]/A), а также S это подмножество P, Подмножество не должно быть непрерывным в P,

У меня есть ощущение, что это может быть сведено к какому-то варианту проблемы с подмножеством сумм, но я действительно не знаю, с чего начать, кроме сортировки P, Цель состоит в том, чтобы реализовать алгоритм в PHP, но на самом деле любой псевдокод очень поможет.

12

aggregate arrays optimization php subset

Решение

Другие решения

Других решений пока нет …

Источник

Accepted Answer

Если вы ищете умное сокращение математики, согласитесь с другими, место математического обмена. В противном случае начните с Math_Combinatorics библиотека. Тогда вы сможете просмотреть все уникальные комбинации S с помощью:

require_once 'Math/Combinatorics.php';
$combos = new Math_Combinatorics;

$P = [1, 5, 3, 6, 4, ...];
for ($n = 1; $n <= count($P); $n++) {
foreach ($combos->combinations($P, $n) as $S) {
... your calculations on S go here ...
}
}

2