Нарисуйте линию фиксированной длины от фиксированной начальной точки к конечной точке
Я застрял в проблеме.
Я пытаюсь решить это за 2 дня. Но я не в курсе.
Это может быть что-то простое, но я просто не знаю, на данный момент & любая помощь приветствуется.
Я хочу сделать линию от A (x1, y1) до B (x2, y2) фиксированной длины.
A.............B
A....B........
A............. B
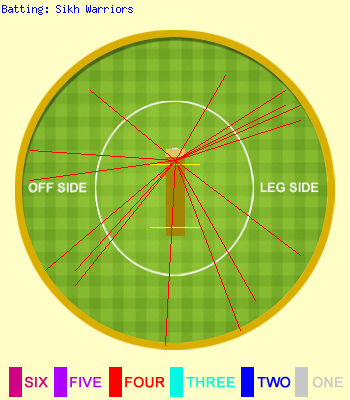
Я сделал мобильный бомбардир крикет. В отчетах он строит колесо телеги.
Поскольку он используется с мобильных устройств, человеческое прикосновение не очень точное, и люди не всегда касаются границы (темно-оранжевый круг на изображении ниже).
Но когда я генерирую отчет в PHP, я должен нарисовать линию от фиксированной начальной точки до границы в направлении, к которому они прикоснулись.
Прямо сейчас мой WAGON WHEEL выглядит следующим образом.
Я перепробовал много способов сделать это, но все не удалось. Теперь моя следующая идея — нарисовать линию фиксированной длины от фиксированной начальной точки (сторона ватина) до координат касания, но фиксированной длины, чтобы линия всегда заканчивалась на границе, независимо от того, является ли касание пользователя не точным.
Я могу рассчитать расстояние между начальной точкой и точкой касания, используя это в php
$lineLength = round( sqrt (pow(($wicketX-$x),2) + pow(($wicketY-$y),2)), 2);
Но я не знаю, как дальше отрегулировать координаты касания до необходимой длины
Пожалуйста, пожалуйста, пожалуйста, помогите.
Постскриптум Этот вопрос выглядел примерно так же, но я понял. Моя математика неделя
Вычислить точку вдоль линии A-B на заданном расстоянии от A
Решение
Я понимаю, что вы хотите найти пересечение линии через точки A и B с кружком. Не нужно быть центром.
Пусть центр круга имеет координаты (Xc, Yc) и радиус будет R,
Любая точка вдоль AB может быть записана как
X = Xa + t (Xb - Xa) = Xc + (Xa - Xc) + t (Xb - Xa) = Xc + Xca + t Xab
Y = Ya + t (Yb - Ya) = Yc + (Ya - Yc) + t (Yb - Ya) = Yc + Yca + t Yab
Вы включаете это в уравнение круга
(X - Xc)² + (Y - Yc)² - R² = (Xca + t Xab)² + (Yca + t Yab)² - R²
= (Xab² + Yab²) t² + 2 (Xca Xab + Yca Yab) t + Xca² + Yca² - R²
= 0
Это уравнение второй степени, которое нужно решить для t, Используйте решение с положительным t, это на стороне Б. От tвычислить (X, Y),
Обратите внимание, что если A является центром, уравнение тривиально сводится к
(Xab² + Yab²) t² = R²
Другие решения
Других решений пока нет …