Найти все четырехугольники между пересекающимися линиями?
Как найти все четырехугольники между несколькими пересекающимися линиями? Единственным условием является то, что каждая сторона четырехугольника является одной линией.
я нашел этот теоретическое объяснение, но не код для него.
До сих пор я в значительной степени в начале. У меня есть свои линии (две точки x, y для каждой линии), и я нашел все их пересечения (точка x, y). Если вы заинтересованы в сценарии, см. Вот.
Пока что мой скрипт основан на php, но я благодарен за любые советы, в том числе и на другом языке.
пример
Здесь множество строк.
line 715.341 0 757.297 600,
line 0 249.169 800 179.178,
line 0 256.196 800 186.205,
line 0 284.225 800 200.142,
line 396.716 0 481.041 600,
line 0 311.374 800 227.29,
line 0 355.76 800 229.053,
line 0 521.525 800 437.442,
line 696.134 0 611.809 600
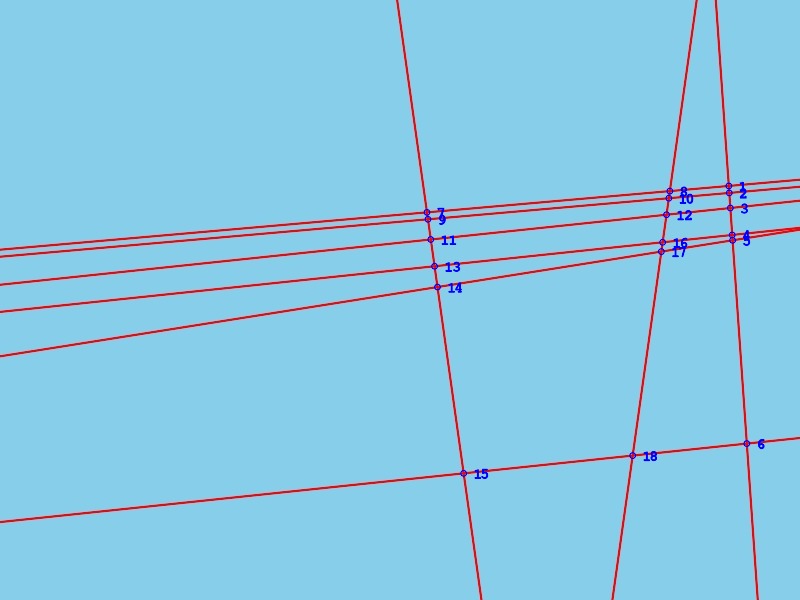
В моем примере точки пересечения будут следующими. Каждая точка имеет число, координаты x и y, а также два идентификатора линии.
Point 1. 728.309, 185.45, 0, 1
Point 2. 728.797, 192.434, 0, 2
Point 3. 729.852, 207.515, 0, 3
Point 4. 731.736, 234.465, 0, 5
Point 5. 732.11, 239.806, 0, 6
Point 6. 746.324, 443.084, 0, 7
Point 7. 426.491, 211.856, 1, 4
Point 8. 669.346, 190.609, 1, 8
Point 9. 427.466, 218.798, 2, 4
Point 10. 668.346, 197.723, 2, 8
Point 11. 430.305, 238.998, 3, 4
Point 12. 666.027, 214.223, 3, 8
Point 13. 434.065, 265.752, 4, 5
Point 14. 436.988, 286.548, 4, 6
Point 15. 463.17, 472.844, 4, 7
Point 16. 662.154, 241.778, 5, 8
Point 17. 660.845, 251.093, 6, 8
Point 18. 632.176, 455.081, 7, 8
convert -size 800x600 xc:skyblue \
-fill red -stroke red -strokewidth 2 \
-draw "line 715.341 0 757.297 600, line 0 249.169 800 179.178, line 0 256.196 800 186.205, line 0 284.225 800 200.142, line 396.716 0 481.041 600, line 0 311.374 800 227.29, line 0 355.76 800 229.053, line 0 521.525 800 437.442, line 696.134 0 611.809 600" \
-font Courier -pointsize 14 -draw "fill none stroke blue circle 728.309,185.45 726.309,183.45 circle 728.797,192.434 726.797,190.434 circle 729.852,207.515 727.852,205.515 circle 731.736,234.465 729.736,232.465 circle 732.11,239.806 730.11,237.806 circle 746.324,443.084 744.324,441.084 circle 426.491,211.856 424.491,209.856 circle 669.346,190.609 667.346,188.609 circle 427.466,218.798 425.466,216.798 circle 668.346,197.723 666.346,195.723 circle 430.305,238.998 428.305,236.998 circle 666.027,214.223 664.027,212.223 circle 434.065,265.752 432.065,263.752 circle 436.988,286.548 434.988,284.548 circle 463.17,472.844 461.17,470.844 circle 662.154,241.778 660.154,239.778 circle 660.845,251.093 658.845,249.093 circle 632.176,455.081 630.176,453.081" \
-draw "fill blue stroke blue text 738.309,190.45 '1' text 738.797,197.434 '2' text 739.852,212.515 '3' text 741.736,239.465 '4' text 742.11,244.806 '5' text 756.324,448.084 '6' text 436.491,216.856 '7' text 679.346,195.609 '8' text 437.466,223.798 '9' text 678.346,202.723 '10' text 440.305,243.998 '11' text 676.027,219.223 '12' text 444.065,270.752 '13' text 446.988,291.548 '14' text 473.17,477.844 '15' text 672.154,246.778 '16' text 670.845,256.093 '17' text 642.176,460.081 '18'" \
lines-intersection.jpg
Итак, теперь большой вопрос, как я использую информацию, чтобы найти все четырехугольники между точками, где каждая сторона — одна линия …
Один из четырехугольников, которые я ищу, это пункты 13, 4, 6 и 15:
Решение
Я бы порекомендовал разбить проблему следующим образом:
- Найти основные четырехугольники в наборе задач
- Найти общие ребра среди этих четырехугольников
- Создайте список или матрицу допустимых комбинаций, чтобы показать все возможные четырехугольники
Найдите основные четырехугольники:
Я бы порекомендовал начать с использования процесса Вороного / Делоне, чтобы найти диаграмму Вороного.
В случае, если вы не знакомы (или другие сталкиваются с этим вопросом, кто не знает), вы пришли к набору точек графа (и соединительных ребер) из набора линий. Диаграмма Вороного определяет набор точек, которые находятся на одинаковом расстоянии от ближайших текущих точек — в основном вы найдете центры закрытых областей, а также некоторые дополнительные элементы. (Более подробное объяснение на Википедия).
Закрытые области (прямоугольники, треугольники и т. Д.), Которые вы хотите, идентифицируются подмножеством точек Вороного, и вы можете выполнить другие тесты, чтобы найти это подмножество программно. Исходя из вашего примера, вы можете или не можете отказаться от полученных треугольников; если вы это сделаете, то вы, вероятно, можете просто посчитать окружающие края / грани, как только вы определили закрытые области.
Я не эксперт по PHP, но мой Google-фу показывает реализацию PHP на GitHub. Моя собственная исследовательская работа посвящена графическим структурам и робототехнике, и такое использование часто встречается.
Одна из интерпретаций диаграммы Вороного состоит в том, что новые точки основаны на «ближайших соседях» — каждая точка лежит в пределах фиксированного или бесконечного многоугольника, созданного исходными точками.
Если вы ищете четырехугольник, то найдите ближайшие 4 точки к каждой точке Вороного. Если есть набор ребер, которые напрямую соединяют 4 точки (pt1-pt2-pt3-pt4-pt1), вы находитесь внутри четырехугольника. Если нет, то вы находитесь в другой форме или в одной из внешних областей, которые ведут к бесконечности.
(Это подход кувалдой, как раньше называл его мой старый аэрокосмический инструктор. Я уверен, что есть более изящные решения, но классификация форм не была тем, что я рассмотрел. Если я найду — или кто-то предложит — лучше Ответ, я буду обновлять это.)
Найти общие ребра среди этих четырехугольников
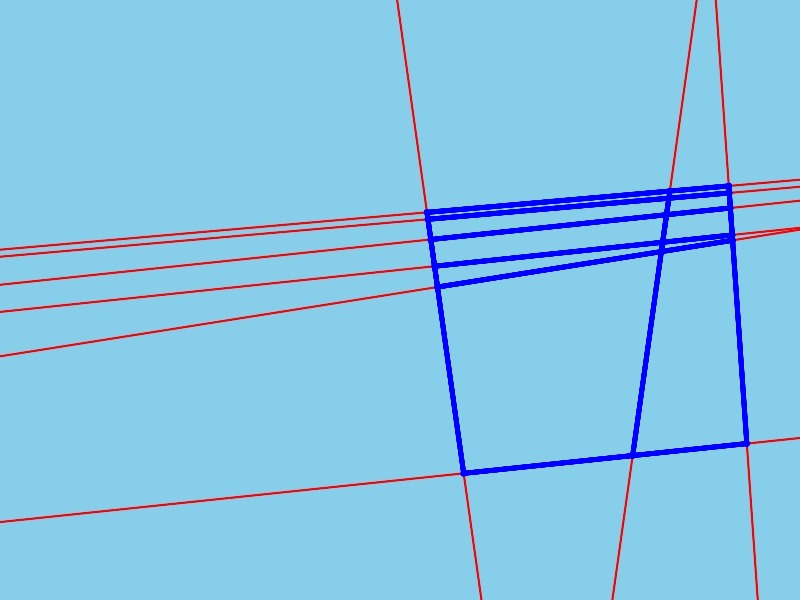
Для «сложенных» четырехугольников, как показано в обновленном вопросе, вы можете найти общие ребра среди основных четырехугольников, а затем составить список комбинаций. Например, если у четырехугольника A есть общая сторона с четырехугольником B, вы создаете четырехугольник большего размера AB.
Составьте список или матрицу допустимых комбинаций После этого вам, вероятно, придется повторно тестировать, пока все возможные комбинации не будут исчерпаны. Одна вещь, которую вы должны будете проверить, это то, что дополнительная фигура все еще является четырехугольником — если вы добавите строку вверх и строку влево или вправо, вы получите фигуру типа «L», которая больше не является допустимой.
Не красиво или элегантно, но, вероятно, эффективно.
Другие решения
Хорошо, я нашел одно решение. К сожалению, я не смог разобраться, используя диаграмму Вороного, рекомендованную angus_thermophyale.
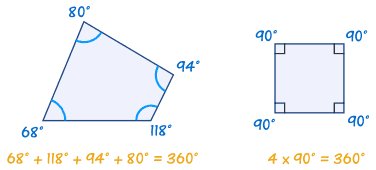
У меня была идея использовать тот факт, что каждый четырехугольник должен иметь суммарный угол 360 °.
В основном я сделал это следующим образом:
- создать список со всеми возможными комбинациями из 4 точек пересечения в цепочке.
- тогда я оправдывал использование каждой комбинации, где две точки находятся на одной линии. Для фильтрации я использовал идентификаторы линий, сохраненные для каждой точки.
- создать векторы между точками и рассчитать углы. Каждый угол должен быть больше 0 ° и меньше 180 °
- Суммируйте 4 угла и проверьте, равен ли он 360 °
Результат
Дайте мне знать, если кто-то заинтересован в деталях кода …