Зачем получать минимальную вершину в алгоритме MST Прима?

Из того, что я понимаю, алгоритм Prim MST будет проходить по всем вершинам графа, выбирая ОДИН лучший край для перемещения к каждой вершине. Следовательно, каждая итерация выберет оптимальную стоимость для каждой соседней вершины. Следовательно, независимо от того, какая вершина используется первой, конечный результат должен быть одинаковым, так как оптимальные затраты выбираются еще до выбора следующей вершины.

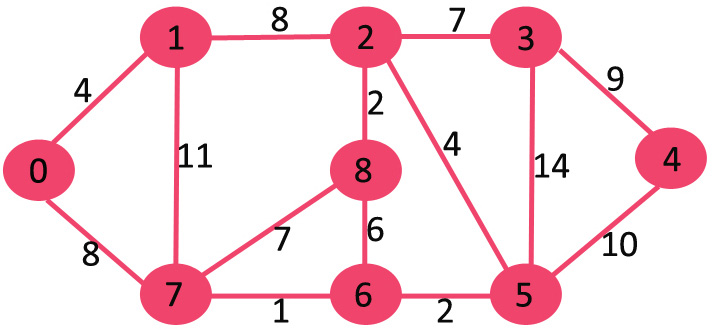
Поэтому я не понимаю, почему алгоритм должен выбирать вершину, которая имеет наименьшую стоимость в каждой итерации. Чтобы сделать мое описание более понятным, я включил пример кода и диаграммы с сайта geeksforgeeks.org:

// A C / C++ program for Prim's Minimum Spanning Tree (MST) algorithm.
// The program is for adjacency matrix representation of the graph

#include <stdio.h>
#include <limits.h>

// Number of vertices in the graph
#define V 5

// A utility function to find the vertex with minimum key value, from
// the set of vertices not yet included in MST
int minKey(int key[], bool mstSet[])
{
// Initialize min value
int min = INT_MAX, min_index;

for (int v = 0; v < V; v++)
if (mstSet[v] == false && key[v] < min)
min = key[v], min_index = v;

return min_index;
}

// A utility function to print the constructed MST stored in parent[]
int printMST(int parent[], int n, int graph[V][V])
{
printf("Edge   Weight\n");
for (int i = 1; i < V; i++)
printf("%d - %d    %d \n", parent[i], i, graph[i][parent[i]]);
}

// Function to construct and print MST for a graph represented using adjacency
// matrix representation
void primMST(int graph[V][V])
{
int parent[V]; // Array to store constructed MST
int key[V];   // Key values used to pick minimum weight edge in cut
bool mstSet[V];  // To represent set of vertices not yet included in MST

// Initialize all keys as INFINITE
for (int i = 0; i < V; i++)
key[i] = INT_MAX, mstSet[i] = false;

// Always include first 1st vertex in MST.
key[0] = 0;     // Make key 0 so that this vertex is picked as first vertex
parent[0] = -1; // First node is always root of MST

// The MST will have V vertices
for (int count = 0; count < V-1; count++)
{
// Pick thd minimum key vertex from the set of vertices
// not yet included in MST
int u = minKey(key, mstSet);

// Add the picked vertex to the MST Set
mstSet[u] = true;

// Update key value and parent index of the adjacent vertices of
// the picked vertex. Consider only those vertices which are not yet
// included in MST
for (int v = 0; v < V; v++)

// graph[u][v] is non zero only for adjacent vertices of m
// mstSet[v] is false for vertices not yet included in MST
// Update the key only if graph[u][v] is smaller than key[v]
if (graph[u][v] && mstSet[v] == false && graph[u][v] <  key[v])
parent[v]  = u, key[v] = graph[u][v];
}

// print the constructed MST
printMST(parent, V, graph);
}// driver program to test above function
int main()
{
/* Let us create the following graph
2    3
(0)--(1)--(2)
|   / \   |
6| 8/   \5 |7
| /     \ |
(3)-------(4)
9          */
int graph[V][V] = {{0, 2, 0, 6, 0},
{2, 0, 3, 8, 5},
{0, 3, 0, 0, 7},
{6, 8, 0, 0, 9},
{0, 5, 7, 9, 0},
};

// Print the solution
primMST(graph);

return 0;
}

Мы можем видеть из следующего блока кода, что каждая итерация будет выбирать оптимальный вес для каждого соседа (в этом случае есть только одно ребро, соединяющее любые две вершины):

if (graph[u][v] && mstSet[v] == false && graph[u][v] < key[v])
parent[v] = u, key[v] = graph[u][v];

Давайте возьмем вершину 7 в качестве примера, она имеет 3 ребра. Ребро 6-7 в конечном итоге будет выбрано из ребер 0-7, 8-7 и 6-7, поскольку его вес минимален, независимо от того, оцениваем ли мы сначала вершины 0-7, 8-7 или 6-7, потому что оптимальный вес = min (вес всех смежных ребер). Следовательно, кажется ненужным выбирать вершину минимального веса на каждой итерации.

Может ли кто-нибудь объяснить мне, какова цель выбора вершины минимального веса для каждой итерации, как в следующем блоке кода?

// Pick thd minimum key vertex from the set of vertices
// not yet included in MST
int u = minKey(key, mstSet);