Yaw, Pitch and roll to glm :: вращаться

Я пытаюсь понять это часами и просто не могу найти решение для этого: я пытаюсь добиться преобразования вектора ориентации в 3 glm::rotation звонки.

У меня есть цилиндр (0, 0, 0) с определенным радиусом и высотой. С помощью Leap Motion SDK я выполняю отслеживание инструмента, которое дает мне положение наконечника и вектор направления (который выражается как единичный вектор, указывающий в том же направлении, что и наконечник):

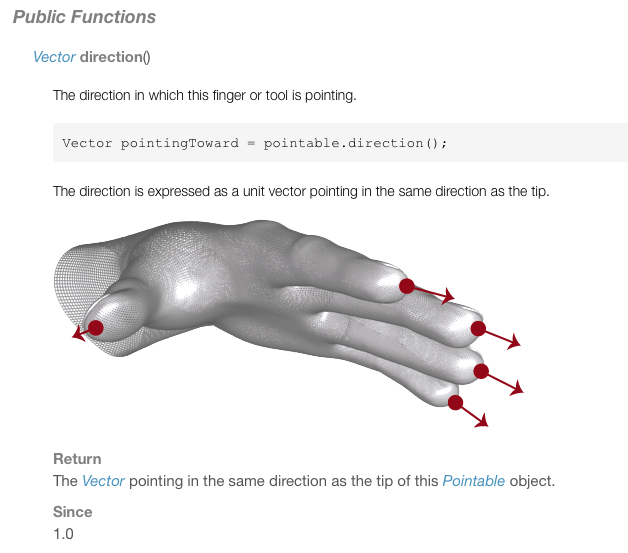
Источник: https://developer.leapmotion.com/documentation/skeletal/java/api/Leap.Pointable.html

Более того, yaw, pitch а также roll можно извлечь из этого вектора следующие функции SDK:

/// The yaw angle in radians.
///
/// Yaw is the angle between the negative z-axis and the projection of
/// the vector onto the x-z plane. In other words, yaw represents rotation
/// around the y-axis. If the vector points to the right of the negative z-axis,
/// then the returned angle is between 0 and pi radians (180 degrees);
/// if it points to the left, the angle is between 0 and -pi radians.
///
/// \image html images/Math_Yaw_Angle.png
///
/// @returns The angle of this vector to the right or left of the negative z-axis.
float yaw() const
{
return std::atan2(x, -z);
}

/// The pitch angle in radians.
///
/// Pitch is the angle between the negative z-axis and the projection of
/// the vector onto the y-z plane. In other words, pitch represents rotation
/// around the x-axis.
/// If the vector points upward, the returned angle is between 0 and pi radians
/// (180 degrees); if it points downward, the angle is between 0 and -pi radians.
///
/// \image html images/Math_Pitch_Angle.png
///
/// @returns The angle of this vector above or below the horizon (x-z plane).
float pitch() const {
return std::atan2(y, -z);
}

/// The roll angle in radians.
///
/// Roll is the angle between the negative y-axis and the projection of
/// the vector onto the x-y plane. In other words, roll represents rotation
/// around the z-axis. If the vector points to the left of the negative y-axis,
/// then the returned angle is between 0 and pi radians (180 degrees);
/// if it points to the right, the angle is between 0 and -pi radians.
///
/// \image html images/Math_Roll_Angle.png
///
/// Use this function to get roll angle of the plane to which this vector is a
/// normal. For example, if this vector represents the normal to the palm,
/// then this function returns the tilt or roll of the palm plane compared
/// to the horizontal (x-z) plane.
///
/// @returns The angle of this vector to the right or left of the y-axis.
float roll() const {
return std::atan2(x, -y);
}

В моем цикле рендеринга OpenGL я извлекаю положение кончика, а также вектор направления для каждого кадра. Я передаю матрицу модели как единую переменную моим шейдерам следующим образом:

cylinder->ResetModelMatrix(); // Set model matrix to identity
glm::vec3 translation = glm::vec3(toolTipPosition.x, toolTipPosition.y, toolTipPosition.z);
cylinder->TranslateModel(translation);
cylinderProgram->SetUniform("modelMatrix", cylinder->GetModelMatrix());

Только с переводом это работает хорошо и выглядит примерно так (цилиндр всегда направлен вверх):

Проблема возникает, когда я пытаюсь повернуть цилиндр в соответствии с ориентацией инструмента Прыжка.
У меня есть следующий код:

yaw = toolDirection.yaw() * Leap::RAD_TO_DEG;
// similarly for pitch and roll

cylinder->Rotate(yaw, glm::vec3(0.0f, 1.0f, 0.0f));
// pitch around (1, 0, 0) and roll around (0, 0, 1)

Однако я не получаю правильную ориентацию, и цилиндр «мерцает» и перепрыгивает между многими ориентациями, когда я пытаюсь применить это.

Важные функции преобразования находятся в интерфейсе, от которого наследуется мой класс цилиндров …

void Drawable::ResetModelMatrix()
{
this->modelMatrix = glm::mat4(1.0f);
}

void Drawable::TranslateModel(glm::vec3 translationVector)
{
this->modelMatrix = glm::translate(this->modelMatrix, translationVector);
}

void Drawable::RotateModel(float angle_in_degrees, glm::vec3 axisOfRotation)
{
this->modelMatrix = glm::rotate(this->modelMatrix, angle_in_degrees, axisOfRotation);
}

void Drawable::ScaleModel(glm::vec3 scalingVector)
{
this->modelMatrix = glm::scale(this->modelMatrix, scalingVector);
}

…с modelMatrix быть переменной-членом.

Я просканировал много похожих вопросов на тему ротации в OpenGL и вообще, но я не совсем уверен, в чем именно проблема с моим кодом.