Высота красно-черного дерева с использованием рекурсии
У меня есть следующие методы, чтобы получить высоту красного черного дерева, и это работает (я отправляю корень). Теперь мой вопрос: как это работает? Я нарисовал дерево и пытался выполнять этот шаг за шагом для каждого рекурсивного вызова, но не могу его осуществить.
Я знаю общую идею того, что делает код, который проходит через все листья и сравнивает их, но может ли кто-нибудь дать четкое объяснение этому?
int RedBlackTree::heightHelper(Node * n) const{
if ( n == NULL ){
return -1;
}
else{
return max(heightHelper(n->left), heightHelper(n->right)) + 1;
}
}
int RedBlackTree::max(int x, int y) const{
if (x >= y){
return x;
}
else{
return y;
}
}
Решение
Итак, общий алгоритм для определения высоты любого двоичного дерева (будь то BST, дерево AVL, красный черный и т. Д.) Выглядит следующим образом
For the current node:
if(node is NULL) return -1
else
h1=Height of your left child//A Recursive call
h2=Height of your right child//A Recursive call
Add 1 to max(h1,h2) to account for the current node
return this value to parent.
Иллюстрация к вышеуказанному алгоритму выглядит следующим образом:
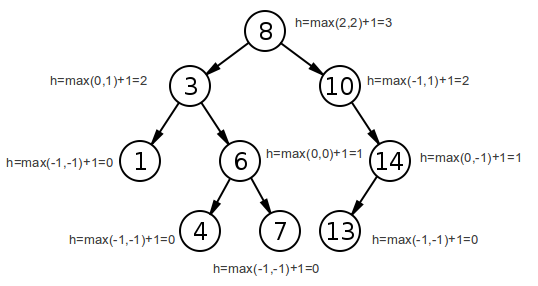
(Изображение предоставлено Wikipedia.org)
Другие решения
Этот код будет возвращать высоту любого двоичного дерева, а не только красно-черного дерева. Работает рекурсивно.
В прошлом мне было трудно думать об этой проблеме, но если мы представим, что у нас есть функция, которая возвращает высоту поддерева, мы могли бы легко использовать ее для вычисления высоты полного дерева. Мы делаем это, вычисляя высоту каждой стороны, беря максимум и добавляя один.
Высота дерева проходит через левую или правую ветвь, поэтому мы можем взять максимум из них. Затем мы добавляем 1 для корня.
Обработка базового случая без дерева (-1), и все готово.
Это основной алгоритм рекурсии.
Начните с базового варианта, если сам корень null высота дерева -1 так как дерево не существует.
Теперь представьте в любом узле, какой будет высота дерева, если этот узел был его корнем?
Это будет просто максимум высоты левого поддерева или правого поддерева (поскольку вы пытаетесь найти максимально возможную высоту, поэтому вам нужно взять большее из 2) и добавить 1 к нему, чтобы включить сам узел ,
Вот и все, как только вы последуете этому, все готово!
Как рекурсивная функция, она вычисляет высоту каждого дочернего узла, используя этот результат для вычисления высоты ток узел, добавив + 1 к этому. Высота любого узла всегда равна максимальной высоте двух дочерних элементов + 1. Случай с одним узлом, вероятно, легче всего понять, поскольку он имеет высоту ноль (0).
A
Здесь стек вызовов выглядит так:
height(A) =
max(height(A->left), height(A->right)) + 1
Так как и левый, и правый являются нулевыми, оба возвращают (-1)и, следовательно, это сводится к
height(A) = max (-1, -1) + 1;
height(A) = -1 + 1;
height(A) = 0
Немного более сложная версия
A
B C
D E
Мы заботимся о рекурсивных вызовах:
height(A) =
max(height(B), height(C)) + 1
height(B) =
max(height(D), height(E)) + 1
Одиночные узлы D, E и C, которые мы уже знаем из нашего первого примера, имеют высоту ноль (у них нет дочерних элементов). поэтому все вышеперечисленное сводится к
height(A) = max( (max(0, 0) + 1), 0) + 1
height(A) = max(1, 0) + 1
height(A) = 1 + 1
height(A) = 2
Я надеюсь, что это, по крайней мере, вредит вам в обучении. Нарисуйте их на бумаге с несколькими образцами деревьев, чтобы лучше понять, если у вас все еще есть сомнения.
