Вычисление медианы в бинарном дереве поиска
Напишите реализацию функции ComputeMedian который вычисляет медианное значение в дереве в O(n) время. Предположим, что дерево является BST, но не обязательно сбалансировано.
Напомним, что медиана из n чисел определяется следующим образом:
Если n нечетно, медиана равна x так, что число значений, меньших x, равно количеству значений, превышающих x. Если n четное, то один плюс число значений, меньших, чем x, равно количеству значений, превышающих x. Например, учитывая цифры
8, 7, 2, 5, 9, медиана равна 7, потому что есть два значения меньше 7 и два значения больше 7. Если мы добавим число 3 в набор, медиана станет 5.
Вот класс двоичного узла дерева поиска:
template <class T>
class BSTNode
{
public:
BSTNode(T& val, BSTNode* left, BSTNode* right);
~BSTNode();
T GetVal();
BSTNode* GetLeft();
BSTNode* GetRight();
private:
T val;
BSTNode* left;
BSTNode* right;
BSTNode* parent; //ONLY INSERT IS READY TO UPDATE THIS MEMBER DATA
int depth, height;
friend class BST<T>;
};
Класс бинарного дерева поиска:
template <class T>
class BST
{
public:
BST();
~BST();
bool Search(T& val);
bool Search(T& val, BSTNode<T>* node);
void Insert(T& val);
bool DeleteNode(T& val);
void BFT(void);
void PreorderDFT(void);
void PreorderDFT(BSTNode<T>* node);
void PostorderDFT(BSTNode<T>* node);
void InorderDFT(BSTNode<T>* node);
void ComputeNodeDepths(void);
void ComputeNodeHeights(void);
bool IsEmpty(void);
void Visit(BSTNode<T>* node);
void Clear(void);
private:
BSTNode<T> *root;
int depth;
int count;
BSTNode<T> *med; // I've added this member data.
void DelSingle(BSTNode<T>*& ptr);
void DelDoubleByCopying(BSTNode<T>* node);
void ComputeDepth(BSTNode<T>* node, BSTNode<T>* parent);
void ComputeHeight(BSTNode<T>* node);
void Clear(BSTNode<T>* node);
};
Я пытался написать эту функцию: я добавил два новых члена данных BSTNode<T>* med а также int count и эта функция вычисляет медиану, только если число элементов нечетное:
template <class T>
T BST<T>::ComputeMedian()
{
BSTNode<T> *median;
int numOfNodes = CountNodes();
if (numOfNodes % 2 != 0) {
count = 0;
ComputeOddMedian(root, numOfNodes/2);
median = med;
return median->val;
}
else {
count = 0;
ComputeEvenMedian(root, numOfNodes/2);
median = med;
return median->val;
}
return -1;
}
template <class T>
void BST<T>::ComputeOddMedian(BSTNode<T> *node, int x)
{
if (node->left) ComputeOddMedian(node->left, x);
count++;
if (count == x+1)
med = node;
if (node->right) ComputeOddMedian(node->right, x);
}
template <class T>
void BST<T>::ComputeEvenMedian(BSTNode<T> *node, int x)
{
if (node->left) ComputeOddMedian(node->left, x);
count++;
if (count == x-1)
med = node;
if (node->right) ComputeOddMedian(node->right, x);
}
Это дает правильные результаты, когда число элементов нечетное, но вызывает ошибки, когда количество элементов четное (я думаю, это потому, что может быть указатель NULL). Я чувствую, что что-то не так в моей реализации, особенно с return в рекурсивных функциях и с добавлением новых членов данных.
Редактировать:
Для нечетного количества предметов:
int main()
{
BST<int> tree;
int x=12;
tree.Insert(x);
x=6;
tree.Insert(x);
x=22;
tree.Insert(x);
x=3;
tree.Insert(x);
x=10;
tree.Insert(x);
cout << tree.ComputeMedian() << endl;
}
Для приведенного выше кода, вывод 10 что является правдой.
Для четного количества предметов:
int main()
{
BST<int> tree;
int x=12;
tree.Insert(x);
x=6;
tree.Insert(x);
x=22;
tree.Insert(x);
x=3;
tree.Insert(x);
x=10;
tree.Insert(x);
x=17;
tree.Insert(x);
cout << tree.ComputeMedian() << endl;
}
Для приведенного выше кода нет выходных данных, и это скриншот для ошибки:
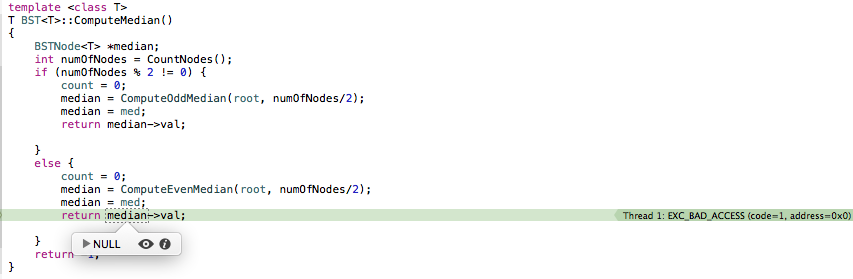
Решение
Задача ещё не решена.
Другие решения
Других решений пока нет …
