Вставить прямоугольник с минимальной фрагментацией

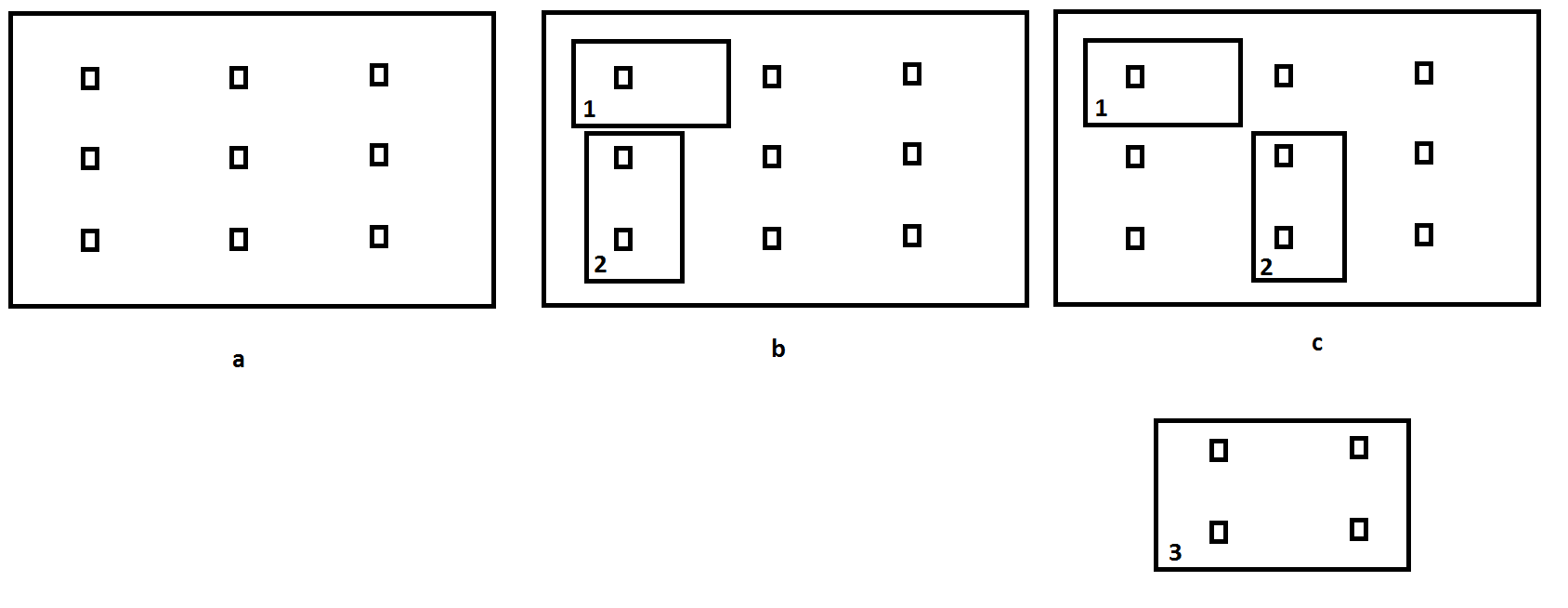
Наличие 2D-бокса с фиксированным положением маленького острия, как на рисунке a. Цель состоит в том, чтобы найти наилучшую позицию для вставки нового прямоугольника прибытия, чтобы облегчить размещение будущих прямоугольников. Предполагается, что каждый прямоугольник, помещенный в поле, должен содержать хотя бы одну точку. Перекрытие между прямоугольниками не допускается.

Например, скажем, после вставки прямоугольника 1 мы должны найти наилучшую позицию для размещения прямоугольника 2. Если мы поместим прямоугольник 2, как на рисунке b, прямоугольник 3 может быть размещен в будущем. Но если мы поместим прямоугольник 2, как на рисунке c, у прямоугольника не будет шансов 3. Поэтому очень важно найти наилучшее решение для вновь поступающего прямоугольника.

Я хотел бы знать, как мы можем оценить положение для нового прямоугольника прибытия, чтобы увеличить возможность размещения для будущих прямоугольников? Есть ли алгоритмы, методы или математические уравнения для этого?

Я думаю о матрице с начальным значением 0 для каждого элемента для представления точек в поле. Когда эта точка занята прямоугольником, соответствующий элемент равен 1, но я не знаю, как выбрать лучшую позицию для нового прибывающего прямоугольника.