Время компиляции вычисляет количество битов, необходимых для кодирования n различных состояний
Редактировать: В первоначальном вопросе была неправильная формула, и алгоритм пытался делать что-то совершенно иное, чем предполагалось. Я прошу прощения и решил переписать вопрос, чтобы устранить всю путаницу.
Мне нужно вычислить во время компиляции (результат будет использоваться как нетипизированный параметр шаблона) минимальное количество бит, необходимое для хранения n разные состояния:
constexpr unsigned bitsNeeded(unsigned n);
или через шаблон
Результаты должны быть:
+-----------+--------+
| number of | bits |
| states | needed |
+-----------+--------+
| 0 | 0 | * or not defined
| | |
| 1 | 0 |
| | |
| 2 | 1 |
| | |
| 3 | 2 |
| 4 | 2 |
| | |
| 5 | 3 |
| 6 | 3 |
| 7 | 3 |
| 8 | 3 |
| | |
| 9 | 4 |
| 10 | 4 |
| .. | .. |
| 16 | 4 |
| | |
| 17 | 5 |
| 18 | 5 |
| .. | .. |
+-----------+--------+
Исходная (как-то исправленная) версия для справки:
Мне нужно вычислить во время компиляции (результат будет использоваться как нетипизированный параметр шаблона) минимальное количество бит, необходимое для хранения n разные состояния, т.е. неотъемлемая часть (округлено вниз) округленный двоичный логарифм:
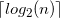
constexpr unsigned ceilLog2(unsigned n);
Это то, что я придумал (совершенно неправильно):
constexpr unsigned intLog2(unsigned num_states_) {
return
num_states_ == 1 ?
1 :
(
intLog2(num_states_ - 1) * intLog2(num_states_ - 1) == num_states_ - 1 ?
intLog2(num_states_ - 1) + 1 :
intLog2(num_states_ - 1)
);
}
Это дает правильный результат (за num_states_ != 0), но рекурсия дует экспоненциально, и это практически непригодный для любого ввода больше 10 (использование памяти во время компиляции превышает 2 ГБ, ОС зависает и происходит сбой компилятора).
Как я могу вычислить это во время компиляции на практике?
Решение
Минимальное количество бит, необходимое для хранения n разные состояния ceil(log2(n)),
constexpr unsigned floorlog2(unsigned x)
{
return x == 1 ? 0 : 1+floorlog2(x >> 1);
}
constexpr unsigned ceillog2(unsigned x)
{
return x == 1 ? 0 : floorlog2(x - 1) + 1;
}
Обратите внимание, что ceillog2(1) == 0, Это прекрасно, потому что если вы хотите сериализовать объект, и вы знаете, что один из его членов данных может принимать только значение 42Вам не нужно ничего хранить для этого участника. Просто назначьте 42 на десериализацию.
Другие решения
Попробуй это:
constexpr unsigned numberOfBits(unsigned x)
{
return x < 2 ? x : 1+numberOfBits(x >> 1);
}
Более простое выражение, правильный результат.
РЕДАКТИРОВАТЬ: «правильный результат», как в «предложенном алгоритме, даже близко не подходит»; конечно, я вычисляю «количество бит для представления значения x»; вычтите 1 из аргумента, если вы хотите знать, сколько бит считать от 0 до x-1. Чтобы представить 1024, вам нужно 11 битов, чтобы считать от 0 до 1023 (1024 состояния), вам нужно 10.
РЕДАКТИРОВАТЬ 2: переименовал функцию, чтобы избежать путаницы.
может быть
constexpr int mylog(int n) {
return (n<2) ?1:
(n<4) ?2:
(n<8) ?3:
(n<16)?4:
(n<32)?5:
(n<64)?6:
…
;
}
так как вы будете использовать его в качестве временного параметра, вы можете проверить, что повышение может предложить
constexpr немного слабоват и будет до C ++ 14. Я рекомендую шаблоны:
template<unsigned n> struct IntLog2;
template<> struct IntLog2<1> { enum { value = 1 }; };
template<unsigned n> struct IntLog2 {
private:
typedef IntLog2<n - 1> p;
public:
enum { value = p::value * p::value == n - 1 ? p::value + 1 : p::value };
};
Из-за путаницы, вызванной первоначальным вопросом, я решил опубликовать этот ответ. Это основано на ответах @DanielKO и @Henrik.
Минимальное количество битов, необходимых для кодирования n разные состояния:
constexpr unsigned bitsNeeded(unsigned n) {
return n <= 1 ? 0 : 1 + bitsNeeded((n + 1) / 2);
}
Что-то, что я использовал в своем собственном коде:
static inline constexpr
uint_fast8_t log2ceil (uint32_t value)
/* Computes the ceiling of log_2(value) */
{
if (value >= 2)
{
uint32_t mask = 0x80000000;
uint_fast8_t result = 32;
value = value - 1;
while (mask != 0) {
if (value & mask)
return result;
mask >>= 1;
--result;
}
}
return 0;
}
Требуется C ++ 14 для использования в качестве constexpr, но у него есть приятное свойство: он достаточно быстр во время выполнения — примерно на порядок быстрее, чем при использовании std::log а также std::ceil— и я проверил, что он дает одинаковые результаты для всех представляемых ненулевых значений (log не определен для нуля, хотя 0 — приемлемый результат для этого приложения; вам не нужны никакие биты для различения нулевых значений), используя следующая программа:
#include <iostream>
#include <cstdlib>
#include <cstdint>
#include <cmath>
#include "log2ceil.hh"
using namespace std;
int main ()
{
for (uint32_t i = 1; i; ++i)
{
// If auto is used, stupid things happen if std::uint_fast8_t
// is a typedef for unsigned char
int l2c_math = ceil (log (i) / log (2));
int l2c_mine = log2ceil (i);
if (l2c_mine != l2c_math)
{
cerr << "Incorrect result for " << i << ": cmath gives "<< l2c_math << "; mine gives " << l2c_mine << endl;
return EXIT_FAILURE;
}
}
cout << "All results are as correct as those given by ceil/log." << endl;
return EXIT_SUCCESS;
}
Это не должно быть слишком сложно обобщать на разные ширины аргументов.
