Установите круг или сплайн в кучу 3D-точек
У меня есть несколько 3D-точек, которые примерно, но четко образуют сегмент круга. Теперь я должен определить круг, который подходит лучше всего по всем точкам. Я думаю, что должен быть какой-то метод наименьших квадратов, который лучше всего подходит, но я не могу понять, с чего начать.
Точки сортируются так, как они будут расположены на круге. У меня также есть предполагаемая кривизна в каждой точке.
Мне нужен радиус и плоскость круга.
Я должен работать в C / C ++ или использовать внешний скрипт.
Решение
Вы могли бы использовать Анализ главных компонентов (PCA), чтобы отобразить ваши координаты от трех измерений до двух измерений.
Вычислите PCA и спроецируйте ваши данные на первый компонент. Затем вы можете использовать любой двухмерный алгоритм, чтобы найти центр круга и его радиус. Как только они будут найдены / установлены, вы можете спроецировать центр обратно в трехмерные координаты.
Поскольку ваши данные зашумлены, в третьем измерении все равно будут некоторые данные, которые вы выдавили, но имейте в виду, что PCA выбирает это измерение, например, чтобы минимизировать количество потерянных данных, то есть путем максимизации количества представляемых данных. в первых двух компонентах, так что вы должны быть в безопасности.
Другие решения
Хороший алгоритм для такой подгонки данных RANSAC (Случайная выборка консенсуса). Вы можете найти хорошее описание в ссылке, так что это лишь краткий обзор важных частей:
В вашем особом случае модель будет 3D круг. Чтобы построить это, выберите три случайные неколинейные точки из вашего набора, вычислите гиперплоскость, в которую они встроены (перекрестное произведение), спроецируйте случайные точки на плоскость, а затем примените обычную 2D-подгонку окружности. При этом вы получите центр круга, радиус и уравнение гиперплоскости. Теперь легко проверить поддержку по каждому из оставшихся пунктов. Опора может быть выражена как расстояние от круга, состоящего из двух частей: ортогональное расстояние от плоскости и расстояние от границы круга внутри плоскости.
Редактировать:
Причина, потому что я предпочел бы RANSAC по сравнению с обычными наименьшими квадратами (LS) — это его превосходящая стабильность в случае тяжелых выбросов. На следующем изображении показан пример сравнения LS с RANSAC. В то время как RANSAC создает идеальную модельную линию, пунктирная линия создается LS.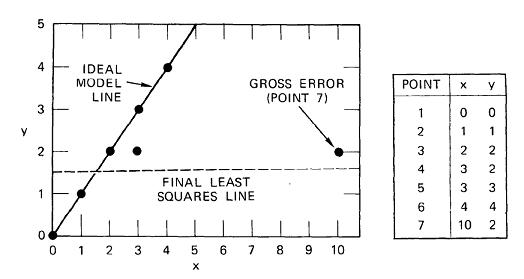
Возможно, самый простой алгоритм называется наименьшей квадратной кривой.
Вы можете проверить математический,
или посмотрите на похожие вопросы, такие как полиномиальные наименьшие квадраты для подгонки кривой изображения
Однако я бы предпочел использовать библиотеку для этого.
