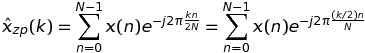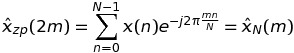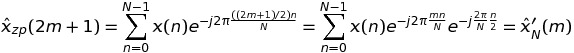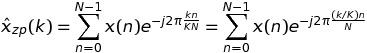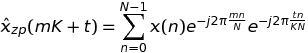Ускорение сокращения FFTW, чтобы избежать массивного заполнения нулями

Question

Ускорение сокращения FFTW, чтобы избежать массивного заполнения нулями

Предположим, что у меня есть последовательность x(n) который K * N долго и только первый N элементы отличаются от нуля. Я предполагаю что N << Kскажем, например, N = 10 а также K = 100000, Я хочу вычислить БПФ, по БПФ, такой последовательности. Это эквивалентно наличию последовательности длины N и с нулевым заполнением K * N, поскольку N а также K может быть «большой», у меня есть существенное заполнение нулями. Я исследую, могу ли я сэкономить некоторое время вычислений, избегая явного заполнения нулями.

Дело K = 2

Давайте начнем с рассмотрения дела K = 2, В этом случае ДПФ x(n) можно записать как

Если k четный, а именно k = 2 * m, затем

это означает, что такие значения ДПФ могут быть вычислены через БПФ последовательности длины N, и не K * N,

Если k странно, а именно k = 2 * m + 1, затем

это означает, что такие значения ДПФ могут быть снова вычислены через БПФ последовательности длины N, и не K * N,

Итак, в заключение я могу обменять один БПФ длины 2 * N с 2 БПФ длины N,

Случай произвольного K

В этом случае мы имеем

Написание k = m * K + t, у нас есть

Итак, в заключение я могу обменять один БПФ длины K * N с K БПФ длины N, Поскольку FFTW имеет fftw_plan_many_dftЯ могу ожидать некоторого выигрыша по сравнению с одним БПФ.

Чтобы убедиться в этом, я настроил следующий код

#include <stdio.h>
#include <stdlib.h>     /* srand, rand */
#include <time.h>       /* time */
#include <math.h>
#include <fstream>

#include <fftw3.h>

#include "TimingCPU.h"
#define PI_d            3.141592653589793

void main() {

const int N = 10;
const int K = 100000;

fftw_plan plan_zp;

fftw_complex *h_x = (fftw_complex *)malloc(N     * sizeof(fftw_complex));
fftw_complex *h_xzp = (fftw_complex *)calloc(N * K, sizeof(fftw_complex));
fftw_complex *h_xpruning = (fftw_complex *)malloc(N * K * sizeof(fftw_complex));
fftw_complex *h_xhatpruning = (fftw_complex *)malloc(N * K * sizeof(fftw_complex));
fftw_complex *h_xhatpruning_temp = (fftw_complex *)malloc(N * K * sizeof(fftw_complex));
fftw_complex *h_xhat = (fftw_complex *)malloc(N * K * sizeof(fftw_complex));

// --- Random number generation of the data sequence
srand(time(NULL));
for (int k = 0; k < N; k++) {
h_x[k][0] = (double)rand() / (double)RAND_MAX;
h_x[k][1] = (double)rand() / (double)RAND_MAX;
}

memcpy(h_xzp, h_x, N * sizeof(fftw_complex));

plan_zp = fftw_plan_dft_1d(N * K, h_xzp, h_xhat, FFTW_FORWARD, FFTW_ESTIMATE);
fftw_plan plan_pruning = fftw_plan_many_dft(1, &N, K, h_xpruning, NULL, 1, N, h_xhatpruning_temp, NULL, 1, N, FFTW_FORWARD, FFTW_ESTIMATE);

TimingCPU timerCPU;
timerCPU.StartCounter();
fftw_execute(plan_zp);
printf("Stadard %f\n", timerCPU.GetCounter());

timerCPU.StartCounter();
double factor = -2. * PI_d / (K * N);
for (int k = 0; k < K; k++) {
double arg1 = factor * k;
for (int n = 0; n < N; n++) {
double arg = arg1 * n;
double cosarg = cos(arg);
double sinarg = sin(arg);
h_xpruning[k * N + n][0] = h_x[n][0] * cosarg - h_x[n][1] * sinarg;
h_xpruning[k * N + n][1] = h_x[n][0] * sinarg + h_x[n][1] * cosarg;
}
}
printf("Optimized first step %f\n", timerCPU.GetCounter());

timerCPU.StartCounter();
fftw_execute(plan_pruning);
printf("Optimized second step %f\n", timerCPU.GetCounter());
timerCPU.StartCounter();
for (int k = 0; k < K; k++) {
for (int p = 0; p < N; p++) {
h_xhatpruning[p * K + k][0] = h_xhatpruning_temp[p + k * N][0];
h_xhatpruning[p * K + k][1] = h_xhatpruning_temp[p + k * N][1];
}
}
printf("Optimized third step %f\n", timerCPU.GetCounter());

double rmserror = 0., norm = 0.;
for (int n = 0; n < N; n++) {
rmserror = rmserror + (h_xhatpruning[n][0] - h_xhat[n][0]) * (h_xhatpruning[n][0] - h_xhat[n][0]) + (h_xhatpruning[n][1] - h_xhat[n][1]) * (h_xhatpruning[n][1] - h_xhat[n][1]);
norm = norm + h_xhat[n][0] * h_xhat[n][0] + h_xhat[n][1] * h_xhat[n][1];
}
printf("rmserror %f\n", 100. * sqrt(rmserror / norm));

fftw_destroy_plan(plan_zp);

}

Подход, который я разработал, состоит из трех этапов:

Умножение входной последовательности на сложную экспоненту
Выполнение fftw_many;
Реорганизация результатов.

fftw_many быстрее, чем один FFTW на K * N точки ввода. Однако шаги № 1 и № 3 полностью уничтожают такой выигрыш. Я ожидал бы, что шаги # 1 и # 3 будут в вычислительном отношении намного легче, чем шаг # 2.

Мои вопросы:

Как это возможно, что шаги № 1 и № 3 так вычислительно более требовательны, чем этап № 2?
Как я могу улучшить шаги № 1 и № 3, чтобы получить чистую прибыль по сравнению со «стандартным» подходом?

Большое спасибо за любой намек.

РЕДАКТИРОВАТЬ

Я работаю с Visual Studio 2013 и компилирую в режиме выпуска.

7

c++fft fftw pruning

Решение

Другие решения

Несколько вариантов, чтобы работать быстрее:

Запускайте многопоточный режим, если вы используете только однопоточный и имеете несколько доступных ядер.
Создайте и сохраните файл мудрости FFTW, особенно если размеры FFT известны заранее. использование FFTW_EXHAUSTIVEи перезагрузите мудрость FFTW вместо того, чтобы пересчитывать ее каждый раз. Это также важно, если вы хотите, чтобы ваши результаты были последовательными. Так как FFTW может вычислять FFT по-разному с разным расчетом, и результаты анализа не обязательно будут всегда одинаковыми, разные прогоны вашего процесса могут давать разные результаты, когда оба получают одинаковые входные данные.
Если вы используете x86, запустите 64-битную версию. Алгоритм FFTW чрезвычайно интенсивно использует регистры, и процессор x86, работающий в 64-битном режиме, имеет гораздо больше регистров общего назначения, чем при работе в 32-битном режиме.
Поскольку алгоритм FFTW требует большого количества регистров, я добился большого успеха в улучшении производительности FFTW, компилируя FFTW с параметрами компилятора, которые предотвращать использование предварительной выборки и предотвращение неявного встраивания функций.

5

Также, следуя комментариям Пола Р., я улучшил свой код. Теперь альтернативный подход быстрее стандартного (с добавлением нуля). Ниже приведен полный скрипт C ++. Для шагов № 1 и № 3 я прокомментировал другие опробованные решения, которые показали, что они медленнее или быстрее, чем некомментированные. Я привел не вложенный for петли, также ввиду более простого будущего распараллеливания CUDA. Я еще не использую многопоточность для FFTW.

#include <stdio.h>
#include <stdlib.h>     /* srand, rand */
#include <time.h>       /* time */
#include <math.h>
#include <fstream>

#include <omp.h>

#include <fftw3.h>

#include "TimingCPU.h"
#define PI_d            3.141592653589793

/******************/
/* STEP #1 ON CPU */
/******************/
void step1CPU(fftw_complex * __restrict h_xpruning, const fftw_complex * __restrict h_x, const int N, const int K) {

//  double factor = -2. * PI_d / (K * N);
//  int n;
//  omp_set_nested(1);
//#pragma omp parallel for private(n) num_threads(4)
//  for (int k = 0; k < K; k++) {
//      double arg1 = factor * k;
//#pragma omp parallel for num_threads(4)
//      for (n = 0; n < N; n++) {
//          double arg = arg1 * n;
//          double cosarg = cos(arg);
//          double sinarg = sin(arg);
//          h_xpruning[k * N + n][0] = h_x[n][0] * cosarg - h_x[n][1] * sinarg;
//          h_xpruning[k * N + n][1] = h_x[n][0] * sinarg + h_x[n][1] * cosarg;
//      }
//  }

//double factor = -2. * PI_d / (K * N);
//int k;
//omp_set_nested(1);
//#pragma omp parallel for private(k) num_threads(4)
//for (int n = 0; n < N; n++) {
//  double arg1 = factor * n;
//  #pragma omp parallel for num_threads(4)
//  for (k = 0; k < K; k++) {
//      double arg = arg1 * k;
//      double cosarg = cos(arg);
//      double sinarg = sin(arg);
//      h_xpruning[k * N + n][0] = h_x[n][0] * cosarg - h_x[n][1] * sinarg;
//      h_xpruning[k * N + n][1] = h_x[n][0] * sinarg + h_x[n][1] * cosarg;
//  }
//}

//double factor = -2. * PI_d / (K * N);
//for (int k = 0; k < K; k++) {
//  double arg1 = factor * k;
//  for (int n = 0; n < N; n++) {
//      double arg = arg1 * n;
//      double cosarg = cos(arg);
//      double sinarg = sin(arg);
//      h_xpruning[k * N + n][0] = h_x[n][0] * cosarg - h_x[n][1] * sinarg;
//      h_xpruning[k * N + n][1] = h_x[n][0] * sinarg + h_x[n][1] * cosarg;
//  }
//}

//double factor = -2. * PI_d / (K * N);
//for (int n = 0; n < N; n++) {
//  double arg1 = factor * n;
//  for (int k = 0; k < K; k++) {
//      double arg = arg1 * k;
//      double cosarg = cos(arg);
//      double sinarg = sin(arg);
//      h_xpruning[k * N + n][0] = h_x[n][0] * cosarg - h_x[n][1] * sinarg;
//      h_xpruning[k * N + n][1] = h_x[n][0] * sinarg + h_x[n][1] * cosarg;
//  }
//}

double factor = -2. * PI_d / (K * N);
#pragma omp parallel for num_threads(8)
for (int n = 0; n < K * N; n++) {
int row = n / N;
int col = n % N;
double arg = factor * row * col;
double cosarg = cos(arg);
double sinarg = sin(arg);
h_xpruning[n][0] = h_x[col][0] * cosarg - h_x[col][1] * sinarg;
h_xpruning[n][1] = h_x[col][0] * sinarg + h_x[col][1] * cosarg;
}
}

/******************/
/* STEP #3 ON CPU */
/******************/
void step3CPU(fftw_complex * __restrict h_xhatpruning, const fftw_complex * __restrict h_xhatpruning_temp, const int N, const int K) {

//int k;
//omp_set_nested(1);
//#pragma omp parallel for private(k) num_threads(4)
//for (int p = 0; p < N; p++) {
//  #pragma omp parallel for num_threads(4)
//  for (k = 0; k < K; k++) {
//      h_xhatpruning[p * K + k][0] = h_xhatpruning_temp[p + k * N][0];
//      h_xhatpruning[p * K + k][1] = h_xhatpruning_temp[p + k * N][1];
//  }
//}

//int p;
//omp_set_nested(1);
//#pragma omp parallel for private(p) num_threads(4)
//for (int k = 0; k < K; k++) {
//  #pragma omp parallel for num_threads(4)
//  for (p = 0; p < N; p++) {
//      h_xhatpruning[p * K + k][0] = h_xhatpruning_temp[p + k * N][0];
//      h_xhatpruning[p * K + k][1] = h_xhatpruning_temp[p + k * N][1];
//  }
//}

//for (int p = 0; p < N; p++) {
//  for (int k = 0; k < K; k++) {
//      h_xhatpruning[p * K + k][0] = h_xhatpruning_temp[p + k * N][0];
//      h_xhatpruning[p * K + k][1] = h_xhatpruning_temp[p + k * N][1];
//  }
//}

//for (int k = 0; k < K; k++) {
//  for (int p = 0; p < N; p++) {
//      h_xhatpruning[p * K + k][0] = h_xhatpruning_temp[p + k * N][0];
//      h_xhatpruning[p * K + k][1] = h_xhatpruning_temp[p + k * N][1];
//  }
//}

#pragma omp parallel for num_threads(8)
for (int p = 0; p < K * N; p++) {
int col = p % N;
int row = p / K;
h_xhatpruning[col * K + row][0] = h_xhatpruning_temp[col + row * N][0];
h_xhatpruning[col * K + row][1] = h_xhatpruning_temp[col + row * N][1];
}

//for (int p = 0; p < N; p += 2) {
//  for (int k = 0; k < K; k++) {
//      for (int p0 = 0; p0 < 2; p0++) {
//          h_xhatpruning[(p + p0) * K + k][0] = h_xhatpruning_temp[(p + p0) + k * N][0];
//          h_xhatpruning[(p + p0) * K + k][1] = h_xhatpruning_temp[(p + p0) + k * N][1];
//      }
//  }
//}

}

/********/
/* MAIN */
/********/
void main() {

int N = 10;
int K = 100000;

// --- CPU memory allocations
fftw_complex *h_x = (fftw_complex *)malloc(N     * sizeof(fftw_complex));
fftw_complex *h_xzp = (fftw_complex *)calloc(N * K, sizeof(fftw_complex));
fftw_complex *h_xpruning = (fftw_complex *)malloc(N * K * sizeof(fftw_complex));
fftw_complex *h_xhatpruning = (fftw_complex *)malloc(N * K * sizeof(fftw_complex));
fftw_complex *h_xhatpruning_temp = (fftw_complex *)malloc(N * K * sizeof(fftw_complex));
fftw_complex *h_xhat = (fftw_complex *)malloc(N * K * sizeof(fftw_complex));
//double2        *h_xhatGPU = (double2 *)malloc(N * K * sizeof(double2));// --- Random number generation of the data sequence on the CPU - moving the data from CPU to GPU
srand(time(NULL));
for (int k = 0; k < N; k++) {
h_x[k][0] = (double)rand() / (double)RAND_MAX;
h_x[k][1] = (double)rand() / (double)RAND_MAX;
}
//gpuErrchk(cudaMemcpy(d_x, h_x, N * sizeof(double2), cudaMemcpyHostToDevice));

memcpy(h_xzp, h_x, N * sizeof(fftw_complex));

// --- FFTW and cuFFT plans
fftw_plan h_plan_zp      = fftw_plan_dft_1d(N * K, h_xzp, h_xhat, FFTW_FORWARD, FFTW_ESTIMATE);
fftw_plan h_plan_pruning = fftw_plan_many_dft(1, &N, K, h_xpruning, NULL, 1, N, h_xhatpruning_temp, NULL, 1, N, FFTW_FORWARD, FFTW_ESTIMATE);

double totalTimeCPU = 0., totalTimeGPU = 0.;
double partialTimeCPU, partialTimeGPU;

/****************************/
/* STANDARD APPROACH ON CPU */
/****************************/
printf("Number of processors available = %i\n", omp_get_num_procs());
printf("Number of threads              = %i\n", omp_get_max_threads());

TimingCPU timerCPU;
timerCPU.StartCounter();
fftw_execute(h_plan_zp);
printf("\nStadard on CPU: \t \t %f\n", timerCPU.GetCounter());

/******************/
/* STEP #1 ON CPU */
/******************/
timerCPU.StartCounter();
step1CPU(h_xpruning, h_x, N, K);
partialTimeCPU = timerCPU.GetCounter();
totalTimeCPU = totalTimeCPU + partialTimeCPU;
printf("\nOptimized first step CPU: \t %f\n", totalTimeCPU);

/******************/
/* STEP #2 ON CPU */
/******************/
timerCPU.StartCounter();
fftw_execute(h_plan_pruning);
partialTimeCPU = timerCPU.GetCounter();
totalTimeCPU = totalTimeCPU + partialTimeCPU;
printf("Optimized second step CPU: \t %f\n", timerCPU.GetCounter());

/******************/
/* STEP #3 ON CPU */
/******************/
timerCPU.StartCounter();
step3CPU(h_xhatpruning, h_xhatpruning_temp, N, K);
partialTimeCPU = timerCPU.GetCounter();
totalTimeCPU = totalTimeCPU + partialTimeCPU;
printf("Optimized third step CPU: \t %f\n", partialTimeCPU);

printf("Total time CPU: \t \t %f\n", totalTimeCPU);

double rmserror = 0., norm = 0.;
for (int n = 0; n < N; n++) {
rmserror = rmserror + (h_xhatpruning[n][0] - h_xhat[n][0]) * (h_xhatpruning[n][0] - h_xhat[n][0]) + (h_xhatpruning[n][1] - h_xhat[n][1]) * (h_xhatpruning[n][1] - h_xhat[n][1]);
norm = norm + h_xhat[n][0] * h_xhat[n][0] + h_xhat[n][1] * h_xhat[n][1];
}
printf("\nrmserror %f\n", 100. * sqrt(rmserror / norm));

fftw_destroy_plan(h_plan_zp);

}

Для случая

N = 10
K = 100000

мое время следующее

Stadard on CPU:                  23.895417

Optimized first step CPU:        4.472087
Optimized second step CPU:       4.926603
Optimized third step CPU:        2.394958
Total time CPU:                  11.793648

1

Источник

Accepted Answer

Для третьего шага вы можете попробовать изменить порядок циклов:

for (int p = 0; p < N; p++) {
for (int k = 0; k < K; k++) {
h_xhatpruning[p * K + k][0] = h_xhatpruning_temp[p + k * N][0];
h_xhatpruning[p * K + k][1] = h_xhatpruning_temp[p + k * N][1];
}
}

поскольку, как правило, выгоднее иметь смежные адреса хранилищ, чем адреса загрузки.

В любом случае, у вас есть недружественный кеш шаблон доступа. Вы можете попробовать работать с блоками, чтобы улучшить это, например. при условии, что N кратно 4:

for (int p = 0; p < N; p += 4) {
for (int k = 0; k < K; k++) {
for (int p0 = 0; p0 < 4; p0++) {
h_xhatpruning[(p + p0) * K + k][0] = h_xhatpruning_temp[(p + p0) + k * N][0];
h_xhatpruning[(p + p0) * K + k][1] = h_xhatpruning_temp[(p + p0) + k * N][1];
}
}
}

Это должно несколько уменьшить отток строк кэша. Если это произойдет, то, возможно, также поэкспериментируйте с размерами блоков, отличными от 4, чтобы увидеть, есть ли «сладкое пятно».

2