уравнение численного анализа
У меня есть это уравнение
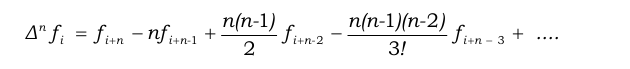
а также
затем найдите полином из
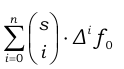
Я пытаюсь реализовать это так:
for (int n=0;n<order;n++){
df[n][0]=y[n];
for (int i=0;i<N;i++){ //N number of points
df[n][i]+=factorial(n,i)*y[i+n-1];
}
}
for (int i=0;i<N;i++){
term=factorial(s,i);
result*=df[0][i]*term;
sum+=result;
}
return sum;
1) Я не уверен, как реализовать знак каждого аргумента в функции. Как вы можете видеть, он становится «положительным», «отрицательным», «положительным» …
2) я не уверен ни в каких ошибках …
Спасибо!
———————-факториал——————————
int fact(int n){
//3!=1*2*3
if (n==0) return 1;
else
return n*fact(n-1);
}
double factorial(double s,int n){
//(s 3)=s*(s-1)*(s-2)/6
if ((n==0) &&(s==0)) return 1;
else
return fact(s)/fact(n);}
Решение
Хорошо, я понимаю, что вы хотите приблизительно вычислить значение f (x) для данного x = X, используя полином Ньютона-интерполяции с равноотстоящими точками (более конкретно, полином Ньютона-Грегори с интерполяцией прямой разности).
Предполагая, что s = (X-x0) / h, где x0 — это первый x, а h — шаг для получения остальной части x, для которой вы знаете точное значение f:
Considere:
double coef (double s, int k)
{
double c(1);
for (int i=1; i<=k ; ++i)
c *= (s-i+1)/i ;
return c;
}
double P_interp_value(double s, int Num_of_intervals , double f[] /* values of f in these points */) // P_n_s
{
int N=Num_of_intervals ;
double *df0= new double[N+1]; // calculing df only for point 0
for (int n=0 ; n<=N ; ++n) // n here is the order
{
df0[n]=0;
for (int k=0, sig=-1; k<=n; ++k, sig=-sig) // k here is the "x point"{
df0[n] += sig * coef(n,k) * f[n-k];
}
}
double P_n_s = 0;
for (int k=0; k<=N ; ++k ) // here k is the order
{
P_n_s += coef(s,k)* df0[k];
}
delete []df0;
return P_n_s;
}int main()
{
double s=0.415, f[]={0.0 , 1.0986 , 1.6094 , 1.9459 , 2.1972 };
int n=1; // Num of interval to use during aproximacion. Max = 4 in these example
while (true)
{
std::cin >> n;
std::cout << std::endl << "P(n=" << n <<", s=" << s << ")= " << P_interp_value(s, n, f) << std::endl ;
}
}
это печать:
1
P (n = 1, s = 0,415) = 0,455919
2
P (n = 2, s = 0,415) = 0,527271
3
P (n = 3, s = 0,415) = 0,55379
4
P (n = 4, s = 0,415) = 0,567235
Оно работает. Теперь мы можем начать оптимизировать этот код.
Другие решения
Самое простое решение, вероятно, состоит в том, чтобы просто сохранить
переменная, и умножьте ее каждый раз через цикл.
Что-то вроде:
sign = 1.0;
for ( int i = 0; i < N; ++ i ) {
term = factorial( s, i );
result *= df[0][i] * term;
sum += sign * result;
sign = - sign;
}
Вы не можете сделать pow( -1, m ),
Вы можете написать свой собственный:
inline int minusOnePower( unsigned int m )
{
return (m & 1) ? -1 : 1;
}
Вы можете создать несколько таблиц рассчитанных значений.
просто для знака 😉
inline signed int minusOnePower( unsigned int m )
{
return 1-( (m & 1)<<1 );
}
