Учитывая начальную популяцию х, что является наименьшим количеством шагов, чтобы добраться до желаемой популяции у
Учитывая начальную популяцию х и точную желаемую популяцию у,
какое наименьшее количество шагов, чтобы добраться до у
используя три функции A {x + 1}, B {x + 2}, C {x + x}
Мой подход
#include<iostream>
using namespace std;
int fA (int x)
{
return x+1;
}
int fB(int x)
{
return x+2;
}
int fC(int x)
{
return x+x;
}
int main()
{
int s, n;
cin>>s>>n;
int counter=0;
while(fC(s)<=n)
{
s=fC(s);
counter++;
}
while(fB(s)<=n)
{
s=fB(s);
counter++;
}
while(fA(s)<=n)
{
s=fA(s);
counter++;
}
cout<<counter;
return 0;
}
Мое предположение о том, что сначала нужно начинать с самой быстрорастущей функции, а после нее — с другой,
Любая помощь приветствуется.
Решение
Одна проблема в том, что то, что является «самым быстрым», зависит от x, Например с x=0 изначально тогда x+x не собирается сильно расти, а также с x=1 самый быстрый x+2не x+x,
Я бы использовал прямой подход полного поиска:
int min_steps(int x, int y) {
std::set<int> active, seen;
active.insert(x); seen.insert(x);
int steps = 0;
while (active.size() && active.find(y) == active.end()) {
// `active` is the set of all populations that we can
// reach in `steps` number of steps or less not greater
// than the target value `y`.
// The next set is computed by starting from every value
// and applying every possible growth function.
// `seen` is the set of all values we saw before to avoid
// adding a value that has been checked before.
steps++;
std::set<int> new_active;
for (std::set<int>::iterator i=active.begin(),e=active.end();
i!=e; ++i) {
for (int f=0; f<3; f++) {
int z;
switch(f) {
case 0: z = *i + 1; break;
case 1: z = *i + 2; break;
case 2: z = *i + *i; break;
}
if (z <= y && seen.find(z) == seen.end()) {
new_active.insert(z);
seen.insert(z);
}
}
}
active = new_active;
}
return active.size() ? steps : -1;
}
Учитывая вид графика количества шагов, чтобы получить от 1 до х с х <= 1000 но я дикий предположение, однако, что есть закрытая форма для решения: выглядит не очевидным, но не полностью случайным …
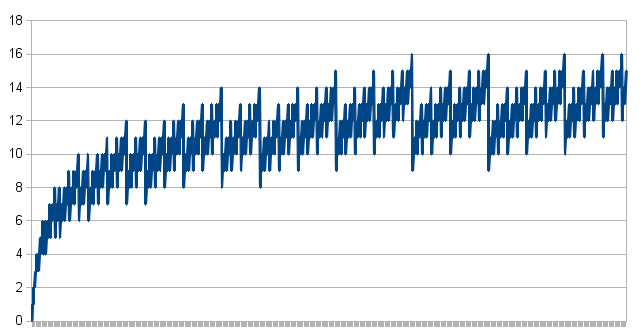
Другие решения
Я опишу общую стратегию с ожиданием максимального количества функциональных приложений. Есть 3 случая. Предположим, х < у во всех случаях. Рассмотрим исходную и целевую численность как битовые строки X и Y.
Случай 1 Если X и Y побитно совпадают в старших значащих битах.
A (x) = x + 1 —-> если младший бит равен 0, изменяет его на 1.
C (x) = x + x = 2 * x —-> сдвигает битовую строку влево на 1
Например
x = 9 and y = 37, so
X = 1001, Y= 100101
Таким образом, сверху вы можете сдвинуть X влево на 2, используя C дважды 9 + 9 —> 18 + 18 —> 36 или
Х = 10010 (18) и затем 100100 (36), а затем прибавить 1, чтобы получить 37.
X = {1001,10010,100100,100101}
Итак, 3 заявки. Таким образом, в случае 1 стратегия будет заключаться в том, чтобы неоднократно применять C и A и строить X, чтобы соответствовать Y поразрядно. Это займет 1 операцию C для каждой смены и 1 A операцию для создания 1. Таким образом, в случае 1 потребуется длина (Y) — длина (X) (количество операций C) + количество единиц в наименее значимой значащей биты Y (операции A). В худшем случае это будут все 1 или 2 * (длина (Y) — длина (X)). В этом случае использование B не помогает.
В худшем случае будет O (длина (Y)) = O (log (у))
Дело 2 (х < 2)
В этом случае использование B добавляет к X быстрее, чем C, а в некоторых случаях (как описано выше) использование B вместо общей стратегии для случая 1 будет на 1 лучше.
Так что, если х = 1 и у = 7, а не
X = {1, 10, 11, 110, 111}, you can skip one step by using B
X = {1, 11, 110, 111}
Случай 3. X и Y несовместимы.
Если X и Y не совпадают в наиболее значимых битах, то вам нужно исправить X, применяя B и A.
пример
X = 110 (6) Y = 101011 (43)
strat X = {110,1000,1010,10100,10101,101010,101011}
Выше X фиксируется для согласования с Y в старших 4 значащих битах, а затем, как только это будет выполнено, используйте страт для случая 1. Свободная верхняя граница будет равна x / 2 (применяя B x / 2 раза = x).
В целом, прогнозируется, что сложность будет O (x) + O (log (y)), что в целом соответствует графику принятого ответа.
