Точка внутри 3D закрытого объема
У меня есть трехмерный замкнутый объем, определяемый 6 поверхностями, каждая поверхность имеет 4 вершины.
Итак, я хочу проверить, находится ли данная точка внутри тома или вне его. Решение, о котором я подумал, было:
-
Нарисуйте случайную линию от заданной точки и проверьте, где она пересекает поверхности, которые охватывают объем. Поскольку я использую векторную алгебру для вычисления пересечения прямой и поверхности, точка пересечения может находиться где угодно на трехмерной бесконечной поверхности.
-
Теперь я проверяю, лежит ли эта точка пересечения на той грани, которая лежит на бесконечной плоскости и охватывает объем.
Для этого я снова хочу нарисовать случайный луч от моей точки пересечения до соответствующей грани объема и проверить, лежит ли точка на грани или нет.
But I don't know how to check this feature of locating if it is on the surface
or not. Can someone please suggest how can I do it.P.S. One way of doing this was extending ray casting to 3d but that involves
comparison of slopes to check the orientation. So how can I check orientation
of 3 points in 3d space. I have 4 vertices which make up that face, I know the
point under consideration. How can I check if this point lies clockwise or
counter clockwise to the surface.
Решение
Чтобы рассмотреть вашу проблему, мы должны сначала рассмотреть, что означает значение внутри или снаружи. С четырьмя твердыми поверхностями каждая поверхность делит пространство ровно на две стороны, и, как правило, четыре поверхности делят пространство на 9 областей, только одна из которых ограничена, ограничивая тетраэдр (но если мы тщательно выберем поверхности, мы можем достичь даже не ограниченной области — например, делая два из них параллельно). Итак, в общем, вы должны решить, какая из сторон плоскостей помечает внутреннюю или внешнюю сторону (ну, это также не имеет значения, поскольку быть снаружи — это то же самое, что не быть внутри).
С большим количеством граней проблема усложняется (и усложняется гораздо больше), поскольку у вас может быть несколько ограниченных областей, которые также определяют твердые тела, поэтому вам нужно больше информации, что только плоскости, которые ее разграничивают. Проблема даже усложняется еще больше, если область приводит к невыпуклой области, потому что ваша точка может находиться в некоторой части вашего региона, которая соответствует в одну сторону для некоторых самолетов и в ту сторону для других, и продолжайте быть внутри вашего тела. Просто посмотрите на такой многоугольник с разделителями
и возможности создания ограниченных областей
Первое, что вам нужно, это адекватно определить ваше тело, разграничив грани с ребрами и несколько установив ребра и вершины, которые разграничивают одну грань, как грани соединяются, чтобы сформировать ваше тело.
Если у вас есть такая ситуация, у вас есть набор граней и векторов, указывающих на вне для каждого лица (непрерывным образом, чтобы вы не заканчивали тем, что лицо обычно направлено вверх, а следующее — вниз). Следующее, что вам нужно сделать, это разделить ваше тело на выпуклое тело. Можно продемонстрировать, что для трехмерного тела, состоящего из простых граней, его можно подразделить на конечный набор выпуклых тел.
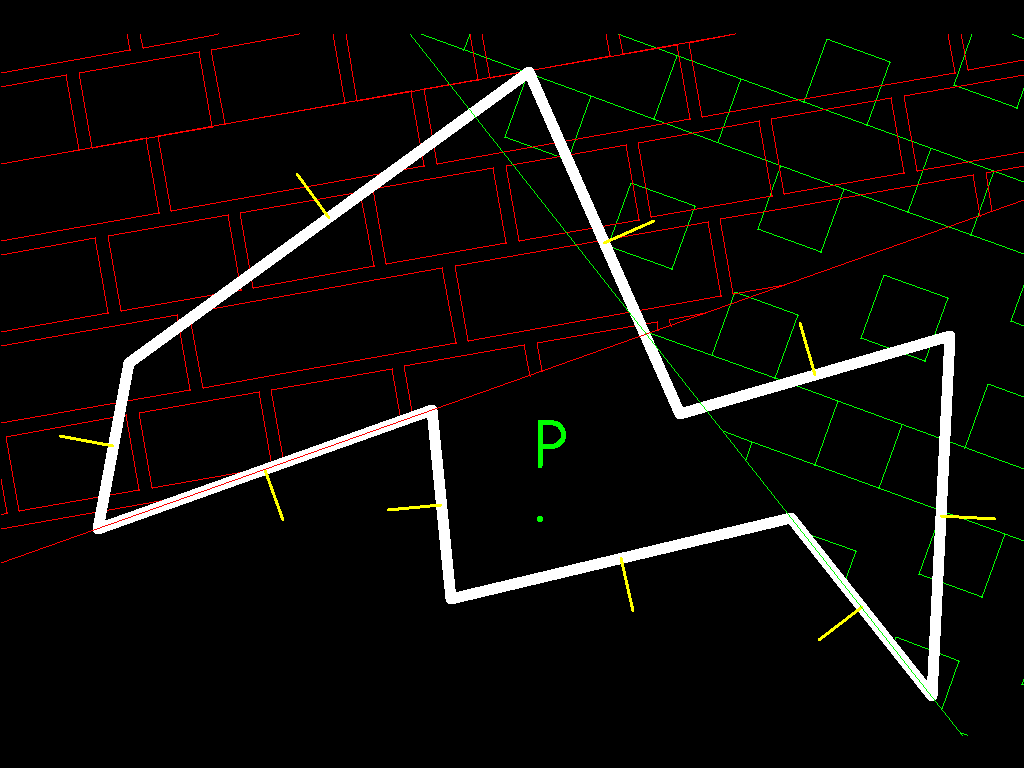
Я попытаюсь проиллюстрировать ту же проблему в 2D, но по сути то же самое в 3D:
Во-первых, у нас есть исходный полигон, давайте предположим, что он выпуклый (это важное свойство для этой цели я упомяну позже):
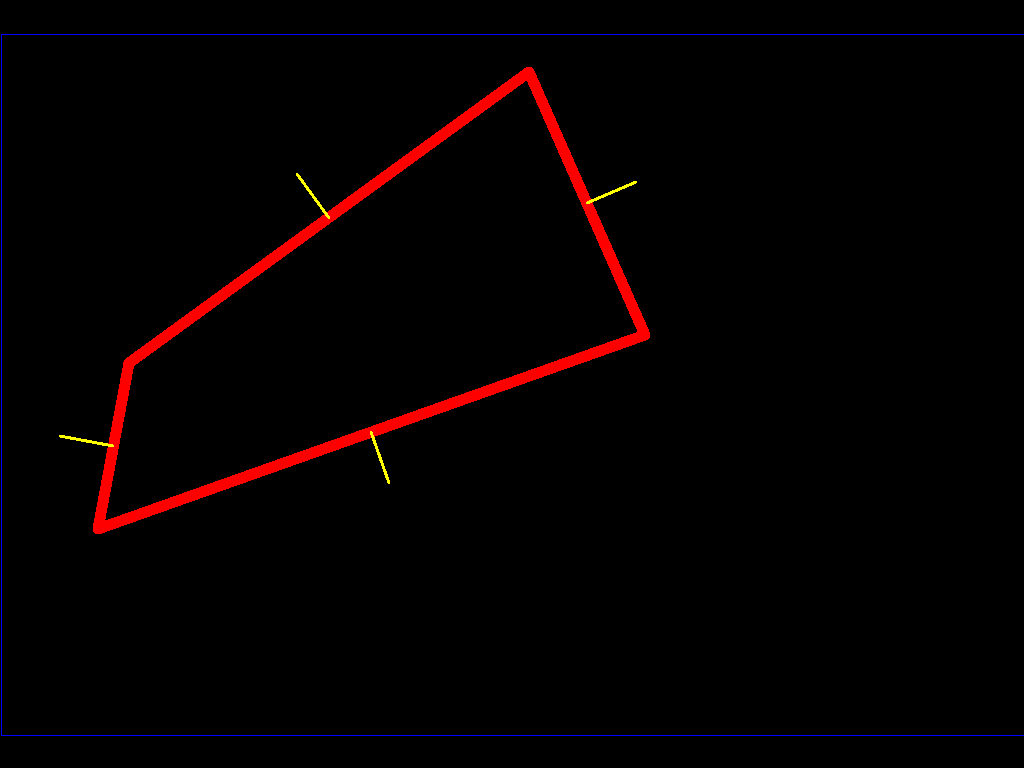
Давайте представим, что это трехмерный астероид, и вы — кто-то, идущий по его поверхности. Если вы начнете ходить, вы пройдете все линии, обозначенные желтым. Это нормали, и для этого вам нужно знать по каждой грани, какие грани достижимы, и построить карту нормали к этим поверхностям, как я сделал. Когда вы идете по астероиду, вы отмечаете нормали, чтобы знать, где находится астероид, и вы разграничиваете его. Теперь у нас есть карта нашего астероида со всеми нормалями. Давайте нарисуем полупространство ниже нас (одна сторона поверхности, которая находится ниже нас). В геометрии это может быть представлено плоскостью (у плоскости есть свойство, что все ее точки ортогональны вектору, поэтому X*V=0 где * представляет собой скалярное произведение. Если мы возьмем центр нашего полигона и вектор нормали в качестве желтого вектора на нашем чертеже, мы получим (X - P)*N = 0, где X положение точки на плоскости, P наша позиция (центр лица) и N является вектором нормали к плоскости, направленной вверх (к внешней стороне астероида)
Ну, это уравнение имеет свойство, что если мы подставим X по любой позиции в пространстве, все точки X ниже плоскости есть значение (X - P)*N < 0 и все значения неба имеют это > 0,
Если я сделаю то же самое для четырех нормалей, я доберусь до этого:
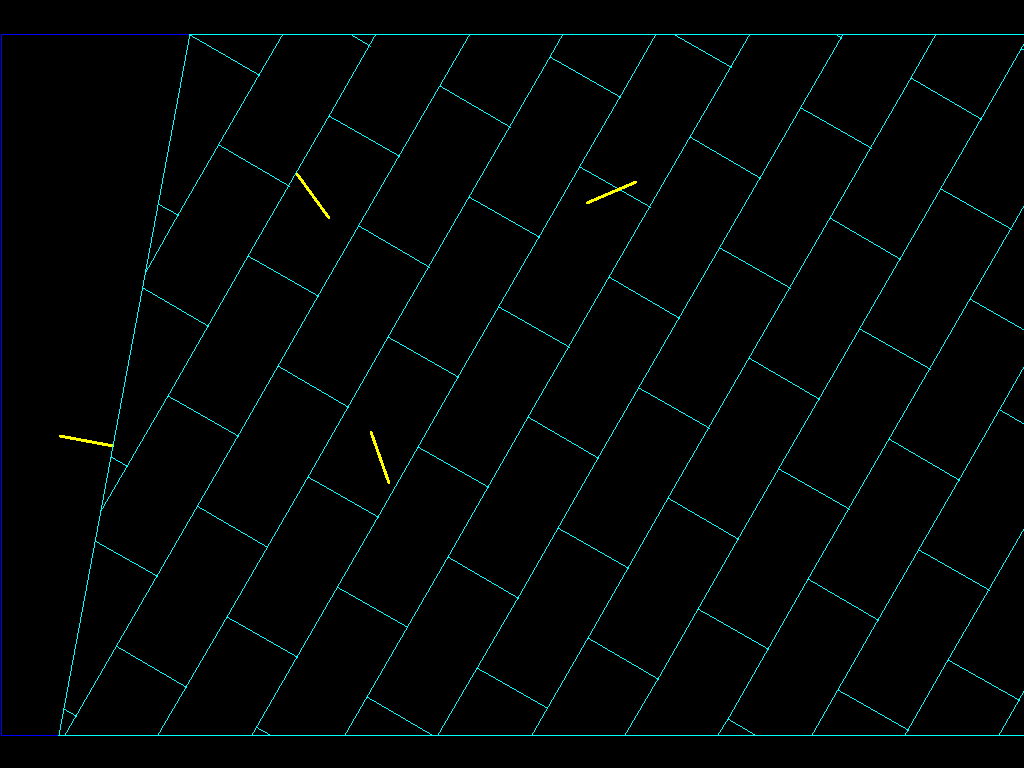
…
иметь дело с
и вопрос X будет похоронен в астероид, только если четыре самолета дают (X - X_face)*(N_face) < 0 где сейчас, X_face центр лица, и N_face это нормальное лицо, указывающее наружу нашего астероида. Точка будет внутри астероида только если применяются четыре условия.
Но что произойдет, если астероид не выпуклый?
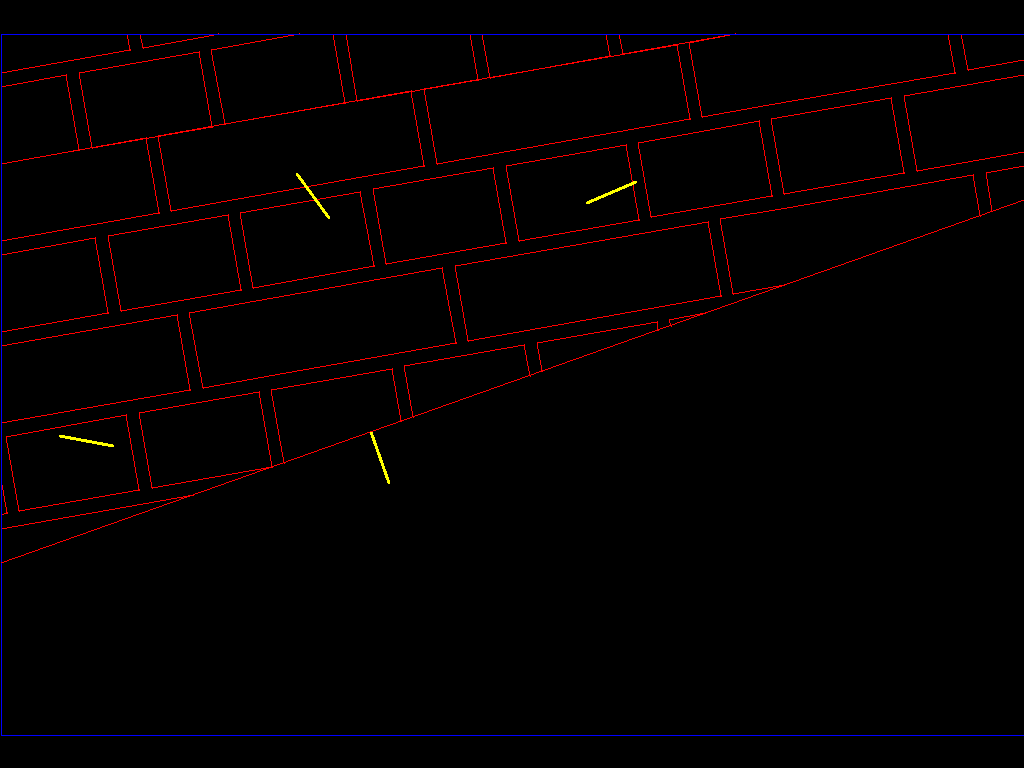
Если вы нарисуете нормали, это не поможет … поскольку есть точки, которые находятся внутри астероида и не проходят некоторые тесты (помните, что точка должна быть ниже всех поверхностей, но это не так (как показано ниже) :
Проблема в том, что многоугольник (или многогранник) не является выпуклым, и мы не можем применить алгоритм там. Итак, сначала мы должны решить проблему выпуклости.
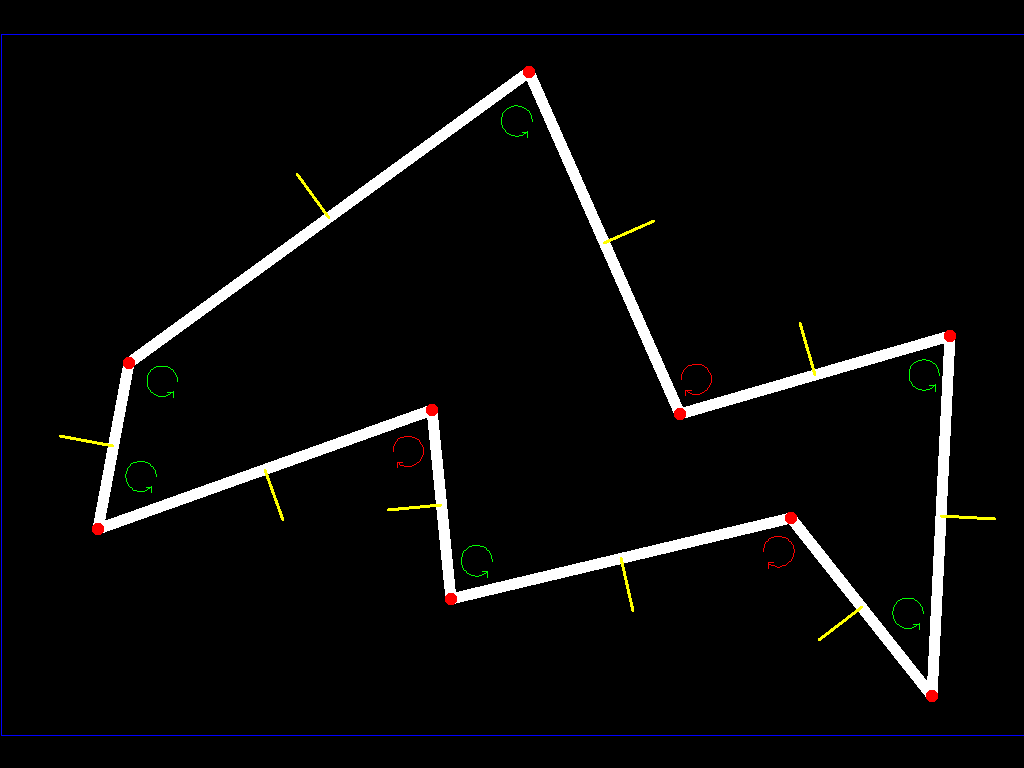
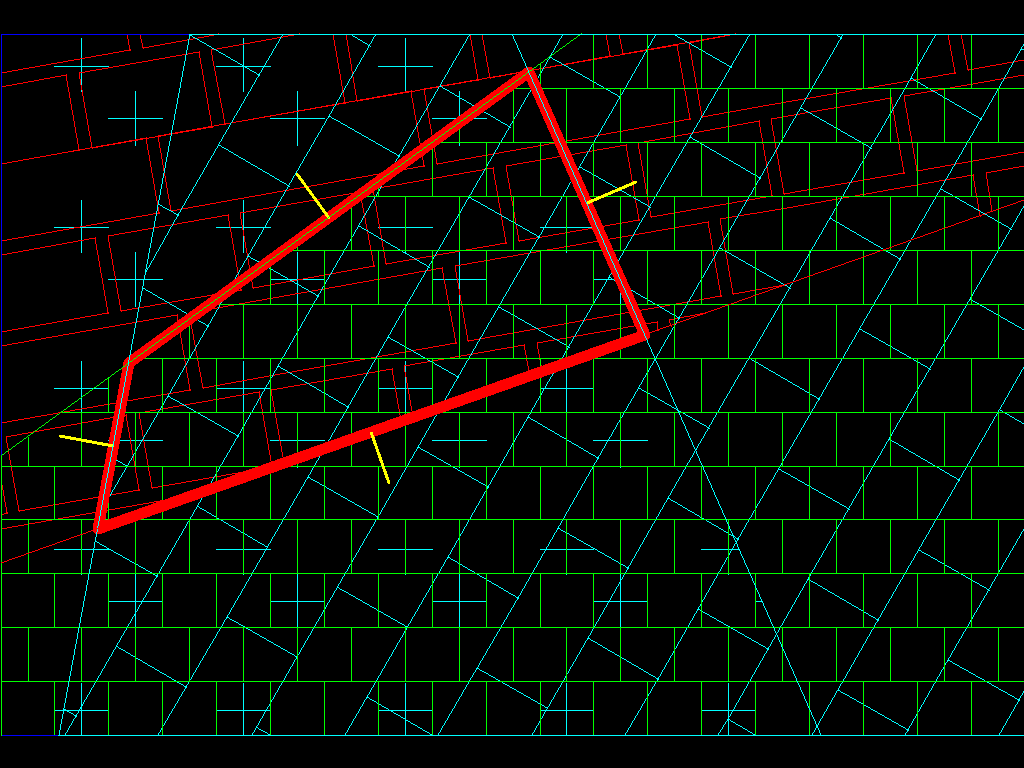
Если вы начнете следовать всей поверхности астероида (сохраняя нормали) при пересечении ребра, вы попадете в другую плоскость, которая увеличивает или уменьшает наклон, поэтому, если он увеличивает наклон, вы отметите этот край (вершину в нашем полигон) как аномальный (мы пометили их красным), и если он уменьшится, мы пометим их как нормальные (мы пометили их зеленым):
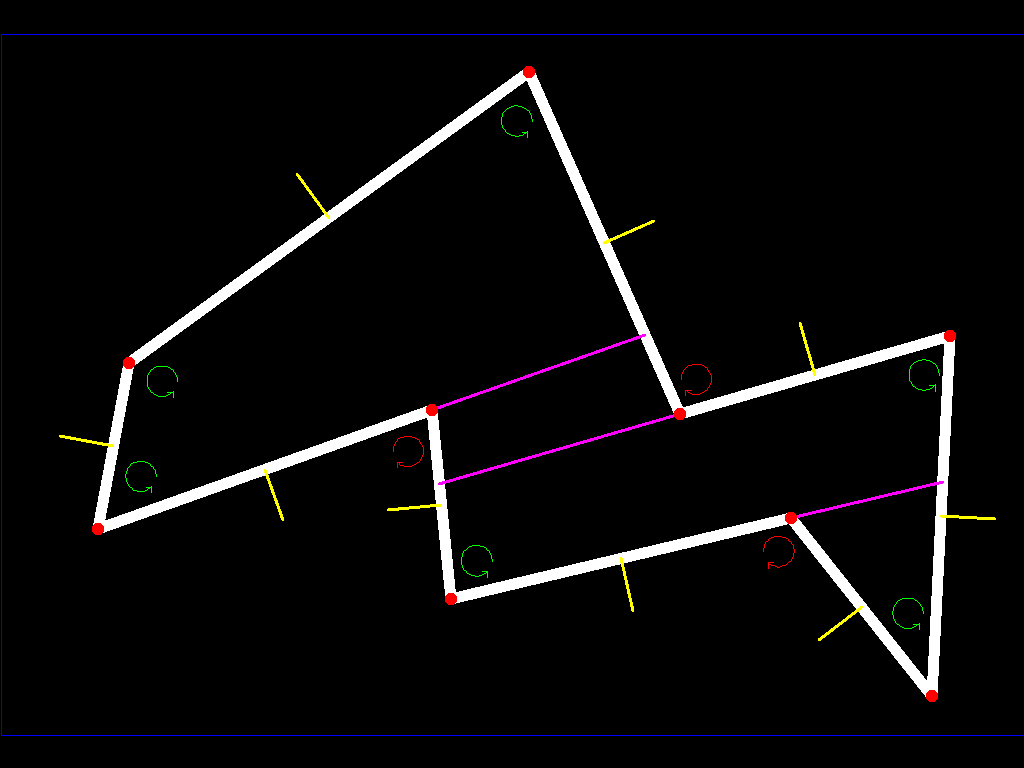
Когда все ребра нормальные, нет проблем, так как наш астероид будет выпуклым, но когда любой из них аномальный, мы должны продолжать в этой плоскости (копаться в астероиде на всей плоскости), пока мы не доберемся до другой поверхности (у нас есть продлил самолет до разделения нашего полигона) как таковой:
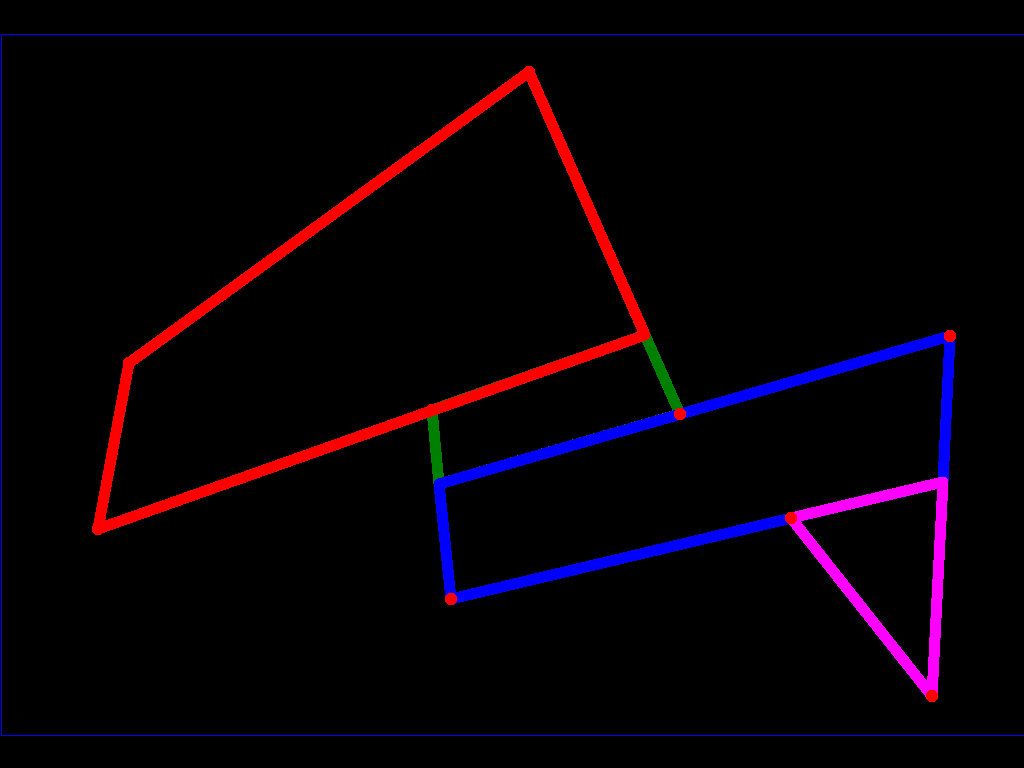
поскольку у нас есть конечное число ребер, и только некоторые из них были помечены как аномальные, этот процесс гарантированно завершен (помните, что вы можете получить Обратная сторона пытаясь найти грань (сторону) вашего многогранника (многоугольника), который имеет вершину вверх и вершину вниз (в смысле, который мы объяснили ранее))
таким образом, вы разделили ваш многогранник на конечный набор выпуклых многогранников, которые можно применить по первому алгоритму.
Другие решения
Вы можете создать логическое условие для каждой поверхности, которое определяет, находится ли данная точка внутри или снаружи поверхности. Для этого может потребоваться добавить информацию о нормалях каждой поверхности (то есть, какая сторона поверхности находится «наружу»). Если это условие выполняется для каждой из шести поверхностей, то точка находится внутри объема.
Еще один похожий способ думать об этом — создать систему линейных неравенств, используя каждую поверхность, чтобы создать одно неравенство, чтобы создать замкнутое пространство, представляющее ваш объем. Это также сводится к удовлетворению того, находится ли точка «внутри» или «снаружи» каждой поверхности, и к проверке, находится ли точка внутри всех поверхностей.
Посмотрите на этот вопрос: расстояние между плоскостью и точкой со знаком
Теперь вам просто нужно проверить, находится ли ваша точка с правой стороны (правильный знак) каждой из ваших поверхностей объема. Что-то вроде этого:
bool isInside(const std::vector<Planes>& planes, const Point& point){
for(const auto& plane : planes){
const auto dist =
dotProduct(plane.normal, vectorSubtract(point, plane.point));
if(dist>0) return false;
}
return true;
};
Итак, один из способов сделать это:
Расширьте приведение лучей к трехмерной поверхности, но это связано с тем, как раз луч из рассматриваемой точки пересек объем. Это включает в себя нахождение точки пересечения линий и граней объема.
So what I can do is for a single face (and I will extend it to all the faces)
is, I check for the point of intersection of 3d line and plane by doing simple
algebra and then check if the point lies inside the cuboid formed by
extremities of the vertices forming the face. i.e check if P(x.y,z) which is
the point of intersection of line and plane lies inside the region defined by
extremities of the surface.
i.e.
x > xlow and x < xhigh and y > ylow and y < yhigh and z > zlow and z < zhigh.
These two conditions i.e. ray intersects the 3d plane and the intersection
lies in this region proves that the intersection of ray and plane lies on the
surface which encloses the volume.I can count the number of such intersections if it is odd, the point
lies inside the volume if it is even the point lies outside the volume.Does anyone see a problem with this algorithm?