string — Найти количество палиндромов, являющихся анаграммами в переполнении стека
Я принимаю участие в онлайн-конкурсе по программированию для развлечения http://www.hackerrank.com. Одна из проблем, над которой я работаю, состоит в том, чтобы найти количество анаграмм строки, которые также являются палиндромами. Я решил проблему, но когда я пытаюсь загрузить ее, она не проходит ряд тестов. Поскольку реальные тестовые примеры скрыты от меня, я не знаю наверняка, почему это не удалось, но я предполагаю, что это может быть проблемой масштабируемости. Теперь я не хочу, чтобы кто-то дал мне готовое решение, потому что это было бы несправедливо, но мне просто интересно, что люди думают о моем подходе.
Вот описание проблемы с сайта:
Теперь, когда король знает, как узнать, имеет ли данное слово анаграмму, являющуюся палиндромом, или нет, он столкнулся с другой проблемой. Он понимает, что может быть несколько анаграмм, которые являются палиндромами для данного слова. Можете ли вы помочь ему узнать, сколько анаграмм возможно для данного слова, которые являются палиндромами?
У короля много слов. Для каждого данного слова король должен узнать количество анаграмм строки, которые являются палиндромами. Поскольку число анаграмм может быть большим, королю нужно количество анаграмм% (109+ 7).
Формат ввода:
Одна строка, которая будет содержать строку вводаВыходной формат :
Одна строка, содержащая количество строк анаграммы, которыеpalindrome % (109 + 7),Ограничения:
1<=length of string <= 105- Каждый символ строки представляет собой строчный алфавит.
- Каждый тестовый пример имеет по крайней мере 1 анаграмму, которая является палиндромом.
Пример ввода 01:
aaabbbbПример вывода 01:
3Пояснение:
Три перестановки данной строки, которые являются палиндромом, могут быть представлены как abbabba, bbaaabb и bababab.Пример ввода 02:
cdcdcdcdeeeefПример вывода 02:
90
Как указано в описании проблемы, входные строки могут достигать 10 ^ 5, поэтому все палиндромы для большой строки невозможны, так как я столкнусь с проблемами насыщения чисел. Кроме того, поскольку мне нужно дать только ответ по модулю (10 ^ 9 + 7), я подумал о том, чтобы взять журнал чисел с основанием (10 ^ 9 + 7) и после всех вычислений взять антилог дробной части с основанием (10 ^ 9). + 7) ответа, так как это все равно будет по модулю.
Мой алгоритм выглядит следующим образом:
- Хранить частоту каждого символа (нужно искать только половину строки, так как
вторая половина должна быть такой же как первая по определению палиндрома) - Если с нечетным числом времени появляется более одного символа, палиндром невозможен
- Иначе для каждой частоты символа постепенно вычисляется число палиндромов (динамическое программирование).
Для DP следующим является подзадача:
previous_count = 1
За каждый дополнительный символ
added number of palindromes = previous_count * (number_of_char_already_seen + 1)/(number of char same as current char)
Вот мой код:
#include <iostream>
#include <string>
#include <vector>
#include <map>
#include <cmath>
#include <cstdio>
#include <algorithm>
#include <fstream>
using namespace std;
#define MAX_SIZE 100001
void factorial2 (unsigned int num, unsigned int *fact) {
fact[num]++;
return;
}
double mylog(double x) {
double normalizer = 1000000007.0;
return log10(x)/log10(normalizer);
}
int main() {
string in;
cin >> in;
if (in.size() == 1) {
cout << 1 << endl;
return 0;
}
map<char, int> freq;
for(int i=0; i<in.size(); ++i) {
if (freq.find(in.at(i)) == freq.end()) {
freq[in.at(i)] = 1;
} else {
freq[in.at(i)]++;
}
}
map<char, int> ::iterator itr = freq.begin();
unsigned long long int count = 1;
bool first = true;
unsigned long long int normalizer = 1000000007;
unsigned long long int size = 0;
unsigned int fact[MAX_SIZE] = {0};
vector<unsigned int> numerator;
while (itr != freq.end()) {
if (first == true) {
first = false;
} else {
for (size_t i=1; i<=itr->second/2; ++i) {
factorial2(i, fact);
numerator.push_back(size+i);
}
}
size += itr->second/2;
++itr;
}
//This loop is to cancel out common factors in numerator and denominator
for (int i=MAX_SIZE-1; i>1; --i) {
while (fact[i] != 0) {
bool not_div = true;
vector<unsigned int> newNumerator;
for (size_t j=0; j<numerator.size(); ++j) {
if (fact[i] && numerator[j]%i == 0) {
if (numerator[j]/i > 1)
newNumerator.push_back(numerator[j]/i);
fact[i]--; //Do as many cancellations as possible
not_div = false;
} else {
newNumerator.push_back(numerator[j]);
}
}
numerator = newNumerator;
if (not_div) {
break;
}
}
}
double countD = 0.0;
for (size_t i=0; i<numerator.size(); ++i) {
countD += mylog(double(numerator[i]));
}
for (size_t i=2; i <MAX_SIZE; ++i) {
if (fact[i]) {
countD -= mylog((pow(double(i), double(fact[i]))));
fact[i] = 0;
}
}
//Get the fraction part of countD
countD = countD - floor(countD);
countD = pow(double(normalizer), countD);
if (floor(countD + 0.5) > floor(countD)) {
countD = ceil(countD);
} else {
countD = floor(countD);
}
count = countD;
cout << count;
return 0;
}
Теперь я потратил много времени на эту проблему, и мне просто интересно, есть ли что-то не так в моем подходе или я что-то здесь упускаю. Есть идеи?
Решение
Основная формула:
p!/(a!*b!...*z!)
где p пол length/2 слова и a, b, c .., z обозначает пол половины частоты вхождений a, b, c .., z в слове восприимчиво.
Единственная проблема, с которой вы сейчас столкнулись — это как рассчитать это. Для этого проверьте этот из.
Другие решения
Обратите внимание, что анаграммы являются рефлексивными (они выглядят одинаково прочитанными сзади и спереди), поэтому половина вхождений каждого символа будет на одной стороне, и нам просто нужно вычислить количество их перестановок. Другая сторона будет точный разворот этой стороны, так что это не добавляет к числу возможностей. Странное вхождение символа (если оно существует) всегда должно быть посередине, поэтому его можно игнорировать при расчете количества перестановок.
Так:
-
Рассчитайте частоты персонажей
-
Проверьте, что есть только 1 нечетная частота
-
Разделите частоту каждого символа (округление вниз — удаляет любое нечетное вхождение).
-
Рассчитайте перестановку этих символов, используя эту формулу:
(согласно Википедия — мультимножественная перестановка)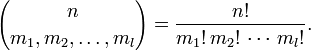
Поскольку приведенные выше термины могут быть довольно большими, мы можем разделить формулу на простые множители, чтобы мы могли отменить термины, чтобы у нас оставалось только умножение, и я думаю, что мы можем % 109 + 7 после каждого умножения, которое должно вписываться в long long (поскольку (109+7)*105 < 9223372036854775807).
Благодаря IVlad для указания на более эффективный метод предотвращения переполнения, чем указано выше:
Заметить, что
p = 109 + 7это простое число, поэтому мы можем использовать Маленькая теорема Ферма вычислить мультипликативные обратныеmi mod pи умножьте на них и возьмите мод на каждом шаге вместо деления.mi-1 = mi(10^9 + 5) (mod p), Используя возведение в квадрат при возведении в квадрат, это будет очень быстро.
Я также нашел этот вопрос (который также имеет несколько полезных дубликатов).
Примеры:
Input: aaabbbb
Frequency:
a b
3 4
Div 2:
a b
1 2
Solution:
3!/2!1! = 3
Input: cdcdcdcdeeeef
Frequency:
c d e f
4 4 4 1
Div 2:
c d e f
2 2 2 0
Solution:
6!/2!2!2!0! = 90
