Столкновение 2D статических ящиков с изменяемой местностью

Я работаю над 2D-игрой, в которой ландшафт может меняться и состоит из любой формы многоугольников, кроме самопересекающихся. Коробка столкновения игрока имеет форму квадрата и может перемещаться. Мой вопрос таков: как мне всегда держать вертикальную коробку, чтобы она сталкивалась с переменной местностью и всегда оставалась снаружи?

Мой нынешний подход, который я составил, хотя никакого кода еще работает, работает следующим образом:

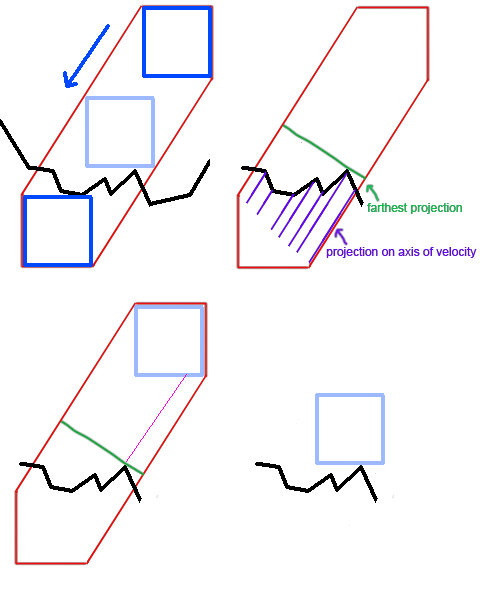
Синий квадрат — это хитбокс игрока. Во-первых, он движется со скоростью вниз в качестве примера. Моя цель состоит в том, чтобы найти самую высокую точку на своем пути, где она может быть безопасно вне полигона местности. Я проверяю все точки вершин ландшафта внутри траектории движения и проецирую их на скорость коробки. Я беру самый дальний прогноз.

Самая дальняя проекция — это максимальное расстояние, на которое можно двигаться, не входя в местность.

Переместить квадрат на расстояние в направлении скорости и готово.

Однако есть несколько сценариев, с которыми я столкнулся, когда это не работает. Возьмите это как пример:

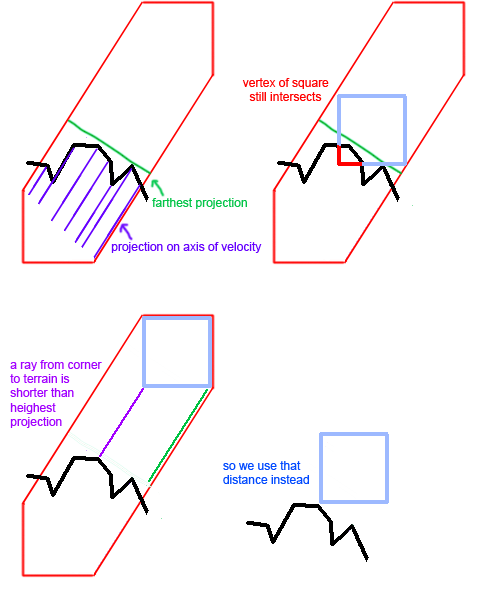
Чтобы исправить эту ситуацию, я сейчас проверяю один угол квадрата. Если расстояние от угла меньше самого дальнего выступа, то это расстояние даст соответствующий сдвиг в расстоянии. Это в значительной степени делает алгоритм полным доказательством. Если кто-то не сформулирует другое исключение.

Я немного схожу с ума, и я был бы признателен за отзыв о моем алгоритме. Если у кого-нибудь есть какие-либо предложения или хорошие отзывы о двухмерных вертикальных столкновениях коробок на местности или чем-то подобном, это было бы здорово.