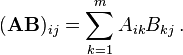Сравнение Python, Numpy, Numba и C ++ для умножения матриц

В программе, над которой я работаю, мне нужно многократно умножить две матрицы. Из-за размера одной из матриц эта операция занимает некоторое время, и я хотел посмотреть, какой метод будет наиболее эффективным. Матрицы имеют размеры (m x n)*(n x p) где m = n = 3 а также 10^5 < p < 10^6,

За исключением Numpy, который, как я предполагаю, работает с оптимизированным алгоритмом, каждый тест состоит из простой реализации умножение матриц:

Ниже приведены мои различные реализации:

питон

def dot_py(A,B):
m, n = A.shape
p = B.shape[1]

C = np.zeros((m,p))

for i in range(0,m):
for j in range(0,p):
for k in range(0,n):
C[i,j] += A[i,k]*B[k,j]
return C

Numpy

def dot_np(A,B):
C = np.dot(A,B)
return C

Numba

Код такой же, как и в Python, но он компилируется как раз перед использованием:

dot_nb = nb.jit(nb.float64[:,:](nb.float64[:,:], nb.float64[:,:]), nopython = True)(dot_py)

До настоящего времени каждый вызов метода был рассчитан с использованием timeit Модуль 10 раз. Лучший результат сохраняется. Матрицы созданы с использованием np.random.rand(n,m),

C ++

mat2 dot(const mat2& m1, const mat2& m2)
{
int m = m1.rows_;
int n = m1.cols_;
int p = m2.cols_;

mat2 m3(m,p);

for (int row = 0; row < m; row++) {
for (int col = 0; col < p; col++) {
for (int k = 0; k < n; k++) {
m3.data_[p*row + col] += m1.data_[n*row + k]*m2.data_[p*k + col];
}
}
}

return m3;
}

Вот, mat2 это пользовательский класс, который я определил и dot(const mat2& m1, const mat2& m2) является функцией друга для этого класса. Это приурочено к использованию QPF а также QPC от Windows.h и программа скомпилирована с использованием MinGW с g++ команда. Опять же, лучшее время, полученное из 10 казней, сохраняется.

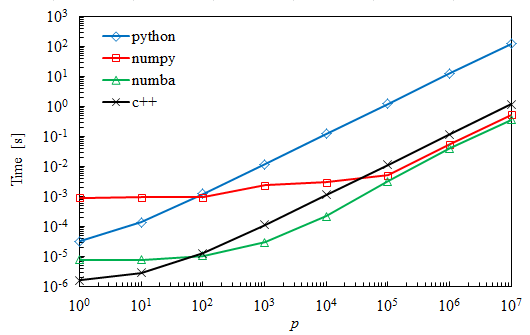
Результаты

Как и ожидалось, простой код на Python медленнее, но он все же превосходит Numpy для очень маленьких матриц. Numba оказывается на 30% быстрее, чем Numpy для самых больших случаев.

Я удивлен результатами C ++, где умножение занимает почти на порядок больше времени, чем с Numba. На самом деле, я ожидал, что это займет столько же времени.

Это приводит к моему основному вопросу: нормально ли это, а если нет, то почему C ++ медленнее, чем Numba? Я только начал изучать C ++, поэтому я могу делать что-то не так. Если так, то в чем заключается моя ошибка или что я могу сделать, чтобы повысить эффективность моего кода (кроме выбора лучшего алгоритма)?

РЕДАКТИРОВАТЬ 1

Вот заголовок mat2 учебный класс.

#ifndef MAT2_H
#define MAT2_H

#include <iostream>

class mat2
{
private:
int rows_, cols_;
float* data_;

public:
mat2() {}                                   // (default) constructor
mat2(int rows, int cols, float value = 0);  // constructor
mat2(const mat2& other);                    // copy constructor
~mat2();                                    // destructor

// Operators
mat2& operator=(mat2 other);                // assignment operator

float operator()(int row, int col) const;
float& operator() (int row, int col);

mat2 operator*(const mat2& other);

// Operations
friend mat2 dot(const mat2& m1, const mat2& m2);

// Other
friend void swap(mat2& first, mat2& second);
friend std::ostream& operator<<(std::ostream& os, const mat2& M);
};

#endif

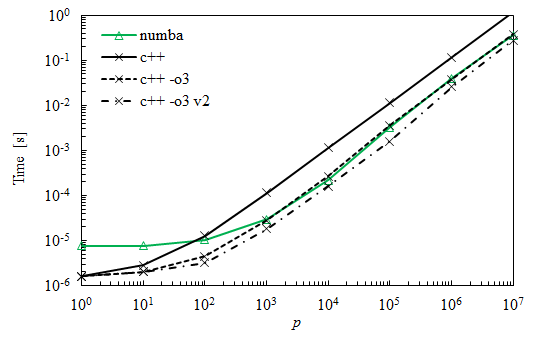
Редактировать 2

Как многие предполагали, использование флага оптимизации было отсутствующим элементом для соответствия Numba. Ниже приведены новые кривые по сравнению с предыдущими. Кривая помечена v2 был получен путем переключения двух внутренних контуров и показывает улучшение еще на 30-50%.