сравнение — Как и почему Комитет по стандартам ISO C ++ (WG21) решил принять предложение об операторе космического корабля таким, какой он есть?

В недавно опубликованной работе [1] Herb Sutter et al. опишите расширение языка программирования C ++ с помощью трехстороннего оператора сравнения. Авторы ссылаются на значительное количество более ранних предложений, все из которых в конечном итоге были отклонены.

Умная основная концепция нового подхода заключается в кодировании различных категорий отношений в типе возврата оператора сравнения. Авторы заявляют, что

Основной целью проекта является концептуальная целостность [Brooks 1975], которая
означает, что дизайн является последовательным и надежно делает то, что пользователь
ожидает, что это сделает.

Всего представлено пять категорий отношений сравнения:

• weak_equality
• strong_equality
• partial_ordering
• weak_ordering
• strong_ordering

Если вам интересно, авторы обосновывают свой выбор слов следующим образом:

Я предложил эти имена вместо стандартных математических терминов
вместо этого, потому что я обнаружил, что этим проще учить.

Из текста можно сделать вывод, что weak_equality соответствует эквивалентность, strong_equality в равенство, weak_ordering в слабый порядок, а также strong_ordering в линейный порядок. В отличие от старых добрых времен [3], авторы, к сожалению, не описывают эти термины аксиоматически.

Это было бы особенно полезно в случае partial_ordering,

Оказывается, что partial_ordering не соответствует частичный заказ в математическом смысле, так как это не навязывает анти-симметрия. Скорее, это соответствует квазиупорядочением.

Оба типа отношений имеют практическое применение.

Широко используемый частичный порядок отношение подмножества. Это очевидно возвратный, переходный, а также анти-симметрична. В частности, для заданных множеств A и B из предложения «A ⊆ B и B ⊆ A» следует, что A и B равны (а не просто эквивалентны).

Это настоящая трагедия, что в совершенно новом контексте невозможно точно представить отношение подмножества (или любой другой частичный порядок).

Для типов с плавающей запятой мы используем partial_ordering который поддерживает оба
ноль со знаком и NaNs, с обычной семантикой, которая -0 <=> +0
возвращается equivalent а также NaN <=> anything возвращается unordered,

В то время как результаты конкретных сравнений с плавающей запятой правильно изображены, авторы пренебрегают тем фактом, что эта конструкция вообще не определяет какой-либо порядок, поскольку в ней отсутствует рефлексивность. Математическая ерунда? Попробуйте отсортировать массив объектов с плавающей запятой, которые содержат NaN, и наслаждайтесь неопределенным поведением!

Другие лазейки представлены в разделе 2.5. Для каждой из категорий отношений сравнения предусмотрена реализация шаблонной функции по умолчанию, в частности:

• strong_order()
• weak_order()
• partial_order()
• strong_equal()
• weak_equal()

Поскольку это средство является чисто библиотечным расширением, нет необходимости беспокоиться об обратной совместимости. Авторы утверждают, что

существующий operator< обычно пытается выразить слабый порядок

Понятно, что они понимают, что не все существующие operator< на самом деле выражает слабый порядок. Тем не менее, реализация по умолчанию weak_order() возвращается к наследию operator== а также operator<и, таким образом, предлагает широкие возможности, чтобы выстрелить себе в ногу во время выполнения.

Это полностью подрывает основные концепции и достойные цели дизайна предложения.

Согласно [4], Комитет по стандартам ISO C ++ (WG21) проголосовал за включение этого предложения в рабочий проект C ++ 20 на совещании в ноябре 2017 года в Альбукерке.

Это приводит к моему вопросу: Осведомлен ли комитет о слабых местах и ​​сознательно принимает их или он просто упустил их из виду?

Чтобы быть уверенным:

• Мне очень нравится базовая концепция.
• Я не вижу никакой выгоды в изменении давно установленных сроков.
• Я не люблю менять значение общих обозначений в тишине без каких-либо четких указаний.
• Мне жаль, что он не предназначен для точного представления частичных заказов.
• Я считаю недопустимым необоснованно подвергать пользователей риску скрытых ошибок времени выполнения.
• Прямое сообщение одному из авторов несколько месяцев назад оставалось без ответа и не принималось во внимание.

Рекомендации

[1] Херб Саттер и др .: Последовательное сравнение.
Документ ISO / IEC JTC1 / SC22 / WG21 P0515R2 (доальбукерская рассылка), 2017–09–30.
URL https://wg21.link/p0515r2

[2] Уолтер Э. Браун: Библиотека поддержки оператора космического корабля (Сравнение). Документ ISO / IEC JTC1 / SC22 / WG21 P0768R0 (доальбукерская рассылка), 2017–09–30.
URL https://wg21.link/p0768r0

[3] Компания Hewlett-Packard: Строгий Слабый Заказ.
Стандартная библиотека шаблонов, Руководство программиста, 1994.
URL https://www.sgi.com/tech/stl/StrictWeakOrdering.html

[4] Botond Ballo: отчет о поездке.
Совещание по стандартам C ++ в Альбукерке, ноябрь 2017 г.
URL https://botondballo.wordpress.com/2017/11/20/trip-report-c-standards-meeting-in-albuquerque-november-2017/

[5] Википедия: Индиана Пи Билл.
URL https://en.wikipedia.org/wiki/Indiana_Pi_Bill

дополнение

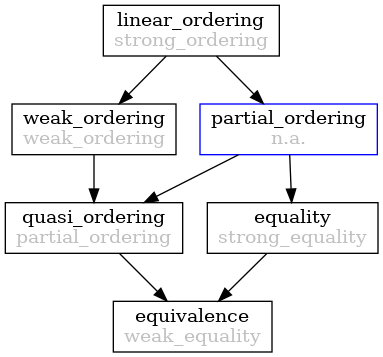
Иерархия, которая содержит истинные частичные порядки, может выглядеть так:

Математически обоснованная реализация именованных функций сравнения из раздела 2.5 может быть такой простой, как:

template <class T>
std::linear_ordering linear_order(const T& a, const T& b)
{
return compare_3way(a, b);
}

template <class T>
std::weak_ordering weak_order(const T& a, const T& b)
{
return compare_3way(a, b);
}

template <class T>
std::partial_ordering partial_order(const T& a, const T& b)
{
return compare_3way(a, b);
}

template <class T>
std::quasi_ordering quasi_order(const T& a, const T& b)
{
return compare_3way(a, b);
}

template <class T>
std::equality equal(const T& a, const T& b)
{
return compare_3way(a, b);
}

template <class T>
std::equivalence equivalent(const T& a, const T& b)
{
return compare_3way(a, b);
}

либо с

template <class T, class U>
auto compare_3way(const T& a, const U& b)
{
return a <=> b;
}

или же

template <class T, class U>
auto compare_3way(const T& a, const U& b)
{
if constexpr (/* can invoke a <=> b */)
{
return a <=> b;
}
else if constexpr (std::is_same_v<T, U> &&
/* can invoke a.M <=> b.M for each member M of T */)
{
/* do that */
}
}

или же

template <class T, class U>
auto compare_3way(const T& a, const U& b)
{
if constexpr (/* can invoke a <=> b */)
{
return a <=> b;
}
else if constexpr (std::is_same_v<T, U> &&
/* can invoke compare_3way(a.M, b.M) for each member M of T */)
{
/* do that */
}
}