Сплайн-интерполяция Безье между двумя узлами: как найти подходящие точки привязки?
В графическом пользовательском интерфейсе я имею дело с графоподобными структурами. Узлы представлены либо кругами, либо прямоугольниками. Пользователь должен иметь возможность рисовать соединительные линии (направленные ребра) между двумя узлами, с возможностью определения набора промежуточных точек, через которые эта линия должна проходить.
Нет проблем в создании кусочно-непрерывной C2-кривой Безье, которая начинается в центре первого узла, проходит через все промежуточные точки и заканчивается в центре второго узла.
проблема
Но теперь (в основном по эстетическим причинам) я хочу, чтобы края начинались / заканчивались на границах узлов, а не на центральных точках. Итак, как я могу найти подходящие точки привязки на границах узлов? Одной из возможностей было бы вычисление точек пересечения между моей кривой Безье и границей узлов. Но для круга это привело бы к полиномиальному уравнению 6-го порядка, и попытка решить это численно кажется излишним.
Возможное решение
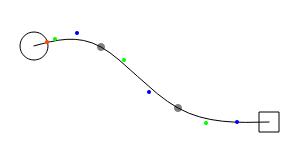
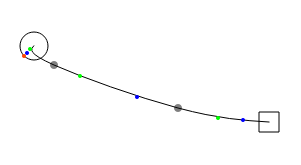
Другой вариант, который я попробовал, — это пересечение границы узла и линии, проходящей через две контрольные точки первой / последней кривой Безье. Хотя это кажется хорошим приближением, если промежуточные точки находятся дальше от узлов, они терпят неудачу, если они находятся близко:
Серый: промежуточные точки, Зеленый, голубой: контрольные точки, красный: приблизительная точка пересечения
Есть ли рекомендуемые способы решения этой проблемы? Как существующие инструменты справляются с этим?
Решение
для круга это привело бы к полиномиальному уравнению 6-го порядка, и попытка решить это численно кажется излишним.
QPainterPath::pointAtPercent можно использовать с простой 1D-схемой Ньютона, чтобы найти пересечение с окружностью. Это действительно легко сделать.
Для квадратов вы можете сделать то же самое, но повторить радиус круга:
-
Начните с круга с центром в центре квадрата, скажем, с той же площадью, что и квадрат.
-
Найти пересечение с кругом.
-
Расширьте новый радиус круга до границы квадрата на линии от центра через точку пересечения, найденную на предыдущем шаге.
-
Повторите с # 2.
Все это легко сделать и должно работать хорошо.
Не берите в голову, что решение полиномиальных уравнений тривиально с чем-то вроде собственного, чтобы сделать алгебру для вас.
Другие решения
Других решений пока нет …