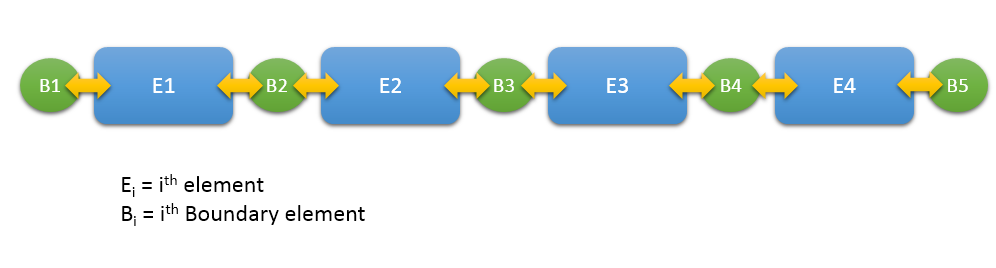
Список Deque с промежуточным замком среди них

Question

Список Deque с промежуточным замком среди них

Я хочу спроектировать структуру данных, в которой у меня есть промежуточные блоки между элементами. Эти замки являются общими для двух соседних элементов.

E (i) — deque, где добавление элемента к нему контролируется B (i) и B (i + 1). Е можно разделить. E (i) и E (i + 1) могут быть объединены в E (i) с удалением B (i + 1). Удаление E запрещено.

Какова будет лучшая структура данных для этого в C ++.

1

c++deque doubly-linked-list heterogeneous-array

Решение

Другие решения

Других решений пока нет …

Источник

Accepted Answer

Стандартная библиотека не имеет разнородных структур данных. У вас есть три подхода: самостоятельно реализовать один, использовать однородную структуру, которая содержит объекты типа тегового объединения, или использовать две параллельные структуры.

Минимальный пример гетерогенного списка:

template<class T,class E>
struct node;

template<class T, class E>
struct edge {
node<T, E> *prev, *next;
E data;
};

template<class T, class E>
struct node {
edge<T, E> *prev, *next;
T data;
};

template<class T, class E>
struct fancy_list {
edge<T, E> *head, *tail;
};

struct wagon {
// wagon members
};
struct boundary {
// boundary members
};

int main() {
fancy_list<wagon, boundary> wagons;
}

Алгоритмы будут работать в основном так же, как алгоритмы для однородных списков, но вам нужно будет разработать стратегию для удаления узлов (один край удален? Какой? Или они объединены? Как?) И вставки (вставить перед или после существующего ребра? Скопируйте существующие ребра в новый или установите состояние по умолчанию?) и т. д. Не существует «правильных» или «лучших» решений без четко определенного варианта использования.

Тэгированная реализация объединения std::variant будет введен в C ++ 17. До тех пор вы должны будете реализовать самостоятельно или зависеть от третьей стороны.

Проблема этого подхода заключается в том, что структура данных по своей сути не обеспечивает инвариант ребер, соседствующих только с узлами, а узлы только с соседними ребрами, поэтому вам все равно придется реализовать свой собственный набор алгоритмов.

Параллельные структуры для ребер и узлов являются типичным способом реализации графа. Ваш список — это просто особый случай графа, который имеет ровно два ребра для каждого узла.

1