Советы по моему графическому проекту
Я работаю над программой, которая будет обновлять список объектов каждые (.1) секунды. После того, как программа закончит обновление списка, программа будет знать, находится ли какой-либо объект на определенном расстоянии от любого другого объекта. Каждый объект имеет позицию X, Y на графике. Каждый объект имеет значение, известное как «Диапазон». Каждый тик (.1s) программа будет использовать формулу расстояния для расчета, если какие-либо другие объекты меньше или равны диапазону обрабатываемого объекта.
Например, если точка A имеет диапазон 4 и находится в точке (1,1), а точка B — в точке (1,2), формула расстояния вернет ~ 1, означая, что точка B находится в пределах диапазона точки A. Расчет будет выглядеть примерно так:
objects = { A = {X = 1,Y = 1,Range = 4}, B = {X = 1,Y = 2,Range = 3}, C = {X = 4,Y = 7,Range = 9} }
while(true) do
for i,v in pairs(objects) do
v:CheckDistance()
end
wait()
end
-- Point:CheckDistance() calculates the distance of all other points from Point "self".
-- Returns true if a point is within range of the Point "self", otherwise false.
--
Эта проблема:
График может содержать более 200 точек, к каждой точке будет применена математическая математика для любой другой существующей точки. Это будет происходить для каждой точки каждые .1с. Я полагаю, что это может замедлить или создать лаг в трехмерной среде, которую я использую.
Вопрос:
Это звучит как оптимальный способ сделать это?
Что вы думаете о том, как это должно быть сделано более эффективно / быстро?
Решение
Как Алекс Фейнам сказал: кажется, вы делаете свой собственный детектор столкновений, хотя и примитивный.
Однако я не уверен, есть ли у вас точки на плоскости 2D или 3D. Вы говорите, что каждый объект «имеет положение X, Y на графике», и далее говорите о «отставании в трехмерной среде, которую я использую».
Ну, как 2D, так и 3D физика, как и Lua, являются хорошо разработанными областями, поэтому нет недостатка в оптимизациях.
квадрантов (или же октодерева для 3D) — это структура данных, которая представляет весь ваш мир в виде квадрата, разделенного на четыре квадрата, каждый из которых разделен на четыре квадрата, и так далее.

Вы можете поэкспериментировать с интерактивным примером самостоятельно на этот удобный сайт.
Пространственные деревья в целом обеспечивают очень быстрый доступ к локализованным точкам.
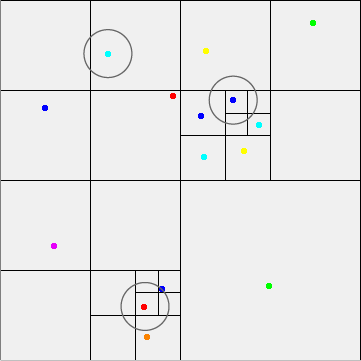
Кружки представляют радиус взаимодействия конкретной частицы. Как видите, легко определить, какие именно ветви необходимо пройти.
При работе с облаками точек вы должны убедиться, что две точки не находятся в одном и том же месте или что у вашего дерева максимальная глубина деления; в противном случае он попытается бесконечно разделить ветви.
Я не знаю ни одной реализации octree в Lua, но ее было бы довольно легко сделать. Если вам нужны примеры, ищите реализацию Python или C; делать не ищите один в C ++, если вы не можете справиться с безумием шаблона.
Кроме того, вы можете использовать реализацию C или C ++ через привязки Lua API или библиотеку FFI (рекомендуется, см. Раздел привязки).
LuaJIT это пользовательский интерпретатор Lua 5.1 и компилятор Just-in-Time, который обеспечивает значительную скорость и оптимизацию хранения, а также библиотеку FFI, которая позволяет легко и эффективно использовать функции и типы Си, такие как целые числа.
Использование типов C для представления ваших точек и пространственного дерева значительно улучшит производительность.
local ffi = require"ffi"ffi.cdef[[
// gp = graphing project
struct gp_point_s {
double x, y;
double range;
};
struct gp_quadtree_root_s {
// This would be extensive
};
struct gp_quadtree_node_s {
//
};
]]
gp_point_mt = {
__add = function(a, b)
return gp_point(a.x+b.x, a.y+b.y)
end,
__tostring = function(self)
return self.x..", "..self.y
end
__index = {
-- I couldn't think of anything you might need here!
something = function(self) return self.range^27 end,
},
}
gp_point = ffi.metatype("struct gp_point_s", gp_point_mt)
-- Now use gp_point at will
local p = gp_point(22.5, 5.4, 6)
print(p)
print(p+gp_point(1, 1, 0))
print(p:something())
LuaJIT будет компилировать любое использование gp_point во время выполнения в нативную сборку, что в некоторых случаях означает C-подобные скорости.
Это хитрый …
Вызовы через API Lua не могут быть должным образом оптимизированы, так как они контролируют состояние Lua.
Принимая во внимание, что необработанные вызовы функций C через FFI LuaJIT могут быть полностью оптимизированы.
Вам решать, как ваш код должен взаимодействовать:
- Прямо в скриптах (Lua, ограничивающий фактор: динамические языки могут быть оптимизированы только до определенной степени)
- Скрипты -> Привязки приложений (Lua -> C / C ++, ограничивающий фактор: Lua API)
- Скрипты -> Внешние библиотеки (Lua -> С, ограничивающий фактор: нет, вызовы FFI скомпилированы JIT)
Не совсем оптимизация, но это важно.
Если вы создаете приложение, предназначенное для взаимодействия с пользователем, то вам не следует исправьте свой временной шаг; то есть вы не можете предполагать, что каждая итерация занимает ровно 0,1 секунды. Вместо этого вы должны умножить все зависящие от времени операции на время.
pos = pos+vel*delta
vel = vel+accel*delta
accel = accel+jerk*delta
-- and so on!
Тем не менее, это физическая симуляция; Есть определенные проблемы с фиксированными и переменными временными шагами для физики, как обсуждал Гленн Фидлер:
Исправь свой временной шаг или взорвись
… Если у вас есть ряд действительно жестких пружинных ограничений для амортизаторов в моделировании автомобиля, то небольшие изменения в dt могут фактически привести к взрыву моделирования. …
Если вы используете фиксированный временной шаг, то симуляция должна теоретически выполняться одинаково каждый раз. Если вы используете переменный шаг по времени, он будет очень плавным, но непредсказуемым. Я бы предложил спросить вашего профессора. (Это университетский проект, верно?)
Другие решения
Я не знаю, возможно ли это в ваших данных обстоятельствах, но я бы определенно использовал события, а не циклы. Это означает отслеживать, когда точка меняет свою позицию, и реагировать на нее. Это гораздо более эффективно, так как требует меньше обработки и обновляет позиции быстрее, чем каждую 1 секунду. Вероятно, вам следует добавить ограничение на количество обращений к функциям, если ваши очки всплывают, потому что тогда будут вызываться эти события. очень довольно часто.
