Сопоставление формы графиков с использованием нелинейных наименьших квадратов
Что было бы лучшим способом реализовать простой алгоритм сопоставления формы, чтобы сопоставить график, интерполированный из 8 точек (x, y), в базу данных похожих графиков (> 12 000 записей), каждый график имеет> 100 узлов. База данных имеет 6 категорий графиков (сигналы измеряются в 6 различных условиях), и главная цель — найти правильную категорию (поэтому для каждой категории есть около 2000 графиков для сравнения).
График из 8 узлов будет представлять фактические данные измерений, но сейчас я имитирую это, выбирая случайный график из базы данных, затем 8 точек из него, а затем размазывая его, используя гауссовский генератор случайных чисел.
Каков наилучший способ реализации нелинейных наименьших квадратов для сравнения формы графика из 8 узлов с каждым графиком из базы данных? Существуют ли какие-либо библиотеки c ++, о которых вы знаете, которые могли бы помочь с этим?
Необходимо ли найти фактическую формулу (f (x)) графика из 8 узлов, чтобы использовать его с наименьшими квадратами, или будет достаточно использовать интерполяцию в запрошенных точках, например, интерполяцию из библиотеки gsl?
Решение
Вы, конечно, можете использовать наименьшие квадраты, не зная фактической формулы. Если все ваши графики измеряются при одном и том же значении x, то это легко — вы просто вычисляете сумму обычным способом:
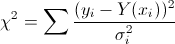
где y_i — точка на графике из 8 узлов, sigma_i — ошибка точки, а Y (x_i) — значение графика из базы данных в той же позиции x, что и y_i. Вы можете понять, почему это тривиально, если все ваши графики измеряются при одном и том же значении x.
Если это не так, вы можете получить Y (x_i), либо подгоняя график из базы данных с помощью некоторой функции (если вы это знаете), либо путем интерполяции между точками (если вы этого не знаете). Самая простая интерполяция — это просто соединить точки прямыми линиями и найти значение прямых линий в желаемой точке x_i. Другие интерполяции может сделать лучше
В моей области мы используем ROOT для такого рода вещей. Тем не мение, SciPy имеет большой набор функций, и вам будет легче начать — если вы не возражаете против использования Python.
Одна из основных проблем, с которой вы можете столкнуться, заключается в том, что эти два графика не являются независимыми. Википедия предлагает испытание Макнемара в этом случае.
Другая проблема, с которой вы можете столкнуться, заключается в том, что у вас недостаточно информации на графике тестирования, поэтому статистические колебания сильно повлияют на ваши результаты. Другими словами, если у вас есть только 8 контрольных точек и совпадают два графика, как вы узнаете, действительно ли базовые функции одинаковы или если 8 точек просто перепрыгнули (внутри своих полос ошибок) таким образом, что это выглядит понравился сюжет из базы — чисто случайно! … Боюсь, ты не узнаешь. Таким образом, графики, которые хорошо тестируют, будут включать в себя ложные срабатывания (низкая чистота), а некоторые из графиков, которые не проходят хорошие тесты, были, вероятно, действительно хорошими совпадениями (низкая эффективность).
Чтобы решить эту проблему, вам нужно будет либо использовать тестовый график с большим количеством точек, либо ввести другую информацию. Если вы можете выбросить из базы данных графики, которые, как вы знаете, не могут совпадать по другим причинам, это очень поможет.
Другие решения
Других решений пока нет …
