solvePnP возвращает неверный результат
Я использую функцию solvePnP для оценки позы моего робота по визуальным маркерам. Иногда я получаю неправильные результаты в двух последовательных кадрах. В файле problem.cpp вы можете увидеть один из этих результатов.
Наборы точек соответствуют одному и тому же маркеру в двух последовательных кадрах. Разница между ними очень мала, а результат solvePnP сильно отличается, но только в векторе вращения. Вектор перевода в порядке.
Это происходит примерно один раз каждые 30 кадров. Я протестировал метод CV_ITERATIVE и CV_P3P с одинаковыми данными, и они возвращают одинаковый результат.
Это пример проблемы:
#include <opencv2/calib3d/calib3d.hpp>
#include <opencv2/core/core.hpp>
#include <iostream>
using namespace std;
using namespace cv;
int main(){
vector<Point2f> points1, points2;
//First point's set
points1.push_back(Point2f(384.3331f, 162.23618f));
points1.push_back(Point2f(385.27521f, 135.21503f));
points1.push_back(Point2f(409.36746f, 139.30315f));
points1.push_back(Point2f(407.43854f, 165.64435f));
//Second point's set
points2.push_back(Point2f(427.64938f, 158.77661f));
points2.push_back(Point2f(428.79471f, 131.60953f));
points2.push_back(Point2f(454.04532f, 134.97353f));
points2.push_back(Point2f(452.23096f, 162.13156f));
//Real object point's set
vector<Point3f> object;
object.push_back(Point3f(-88.0f,88.0f,0));
object.push_back(Point3f(-88.0f,-88.0f,0));
object.push_back(Point3f(88.0f,-88.0f,0));
object.push_back(Point3f(88.0f,88.0f,0));
//Camera matrix
Mat cam_matrix = Mat(3,3,CV_32FC1,Scalar::all(0));
cam_matrix.at<float>(0,0) = 519.0f;
cam_matrix.at<float>(0,2) = 320.0f;
cam_matrix.at<float>(1,1) = 522.0f;
cam_matrix.at<float>(1,2) = 240.0f;
cam_matrix.at<float>(2,2) = 1.0f;
//PnP
Mat rvec1i,rvec2i,tvec1i,tvec2i;
Mat rvec1p,rvec2p,tvec1p,tvec2p;
solvePnP(Mat(object),Mat(points1),cam_matrix,Mat(),rvec1i,tvec1i,false,CV_ITERATIVE);
solvePnP(Mat(object),Mat(points2),cam_matrix,Mat(),rvec2i,tvec2i,false,CV_ITERATIVE);
solvePnP(Mat(object),Mat(points1),cam_matrix,Mat(),rvec1p,tvec1p,false,CV_P3P);
solvePnP(Mat(object),Mat(points2),cam_matrix,Mat(),rvec2p,tvec2p,false,CV_P3P);
//Print result
cout<<"Iterative: "<<endl;
cout<<" rvec1 "<<endl<<" "<<rvec1i<<endl<<endl;
cout<<" rvec2 "<<endl<<" "<<rvec2i<<endl<<endl;
cout<<" tvec1 "<<endl<<" "<<tvec1i<<endl<<endl;
cout<<" tvec1 "<<endl<<" "<<tvec2i<<endl<<endl;
cout<<"P3P: "<<endl;
cout<<" rvec1 "<<endl<<" "<<rvec1p<<endl<<endl;
cout<<" rvec2 "<<endl<<" "<<rvec2p<<endl<<endl;
cout<<" tvec1 "<<endl<<" "<<tvec1p<<endl<<endl;
cout<<" tvec1 "<<endl<<" "<<tvec2p<<endl<<endl;
return 0;
}
И вот результат:
Iterative:
rvec1
[-0.04097605099283788; -0.3679435501353919; 0.07086072250132323]
rvec2
[0.4135950235376482; 0.6834759799439329; 0.1049879790744613]
tvec1
[502.4723979671957; -582.21069174737; 3399.430492848247]
tvec2
[774.9623278021523; -594.8332356366083; 3338.42153723169]
P3P:
rvec1
[-0.08738607323881876; -0.363959462471951; 0.06617591006606272]
rvec2
[0.4239629869157338; 0.7210136877984544; 0.1133539043199323]
tvec1
[497.3941378807597; -574.3015171812298; 3354.522829883918]
tvec1
[760.2641421675842; -582.2718972605966; 3275.390313948845]
Благодарю.
Решение
Я предполагаю, что ваши входные изображения 640×480 и нанесите два наблюдаемых маркера на белый холст. Маркер из первого кадра красный, а маркер из второго кадра синий.

Квадрат примерно совпадает с камерой на обоих изображениях и довольно мал на экране. Это означает, что очень трудно оценить положение и вращение. Особенно расстояние до объекта и вращение вокруг осей X и Y. Умеренное изменение поворота вокруг этих осей вряд ли будет вообще заметно, поскольку точки будут в основном перемещаться к камере или от нее. Ошибки при обнаружении маркера будут иметь большое влияние на результат.
Неопределенность в оцененном положении маркера и ориентации может быть оценена с использованием якобиана, полученного из projectPoints метод.
// Compute covariance matrix of rotation and translation
Mat J;
vector<Point2f> p;
projectPoints(object, rvec1i, tvec1i, cam_matrix, Mat(), p, J);
Mat Sigma = Mat(J.t() * J, Rect(0,0,6,6)).inv();
// Compute standard deviation
Mat std_dev;
sqrt(Sigma.diag(), std_dev);
cout << "rvec1, tvec1 standard deviation:" << endl << std_dev << endl;
rvec1, стандартное отклонение tvec1:
[0,0952506404906549; +0,09211686006979068; +0,02923763901152477; +18,61834775099151; +21,61443561870643; +124,9111908058696]
Полученное здесь стандартное отклонение следует масштабировать с учетом неопределенности наблюдаемых точек (в пикселях). Вы можете видеть, что неопределенность вращения вокруг x и y больше, чем вокруг z, и что расстояние до камеры имеет очень большую неопределенность.
Если вы скопируете результат в Matlab, вы можете построить ковариационную матрицу следующим образом:
imagesc(sqrt(abs(Sigma)))
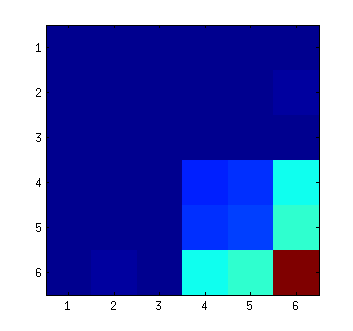
Изображение говорит нам, что неопределенность является самой большой в поступательном направлении z и что оценка в этом направлении довольно сильно связана с оценками положения x и y (в трехмерном пространстве). Поскольку вращение и перемещение используют разные единицы, сложнее связать ошибки вращения с ошибками в положении.
Если вы хотите более стабильные оценки маркера, я бы предложил отфильтровать данные с Расширенный фильтр Калмана или что-то подобное. Это позволит вам извлечь выгоду из знания того, что изображения являются частью последовательности, и отслеживать неопределенность, чтобы вас не обманули наблюдения с небольшим количеством информации. OpenCV имеет некоторые функции для Фильтрация Калмана это может пригодиться.
Возможно, вы уже давно решили свои проблемы, но я надеюсь, что этот пост поможет кому-то понять!
Другие решения
Других решений пока нет …
