Случайные леса выполняются в ожидании
Я изучаю алгоритм дерева решений и реализовал случайный лес, ссылаясь на RF в Weka. Я протестировал и мою реализацию, и реализацию weka (в настройках по умолчанию) с одним и тем же набором данных. Однако моя точность была примерно на 5% ниже, чем точность, полученная в Weka версии 3.8 (полученной с помощью обучающего набора train-first1000.arff и тестового набора dev-first1000.arff).
Набор данных формата arff, который я использовал, был обзорами фильмов от IMDb. Для каждого экземпляра он содержит ряд частот самых популярных слов и был помечен либо «P» (для положительного), либо «N» (для отрицательного).
Для сравнения я использовал настройки по умолчанию в случайных лесах Weka (100 деревьев, log () + 1 функция, учитываемая при разделении, никаких мешков и т. Д.)
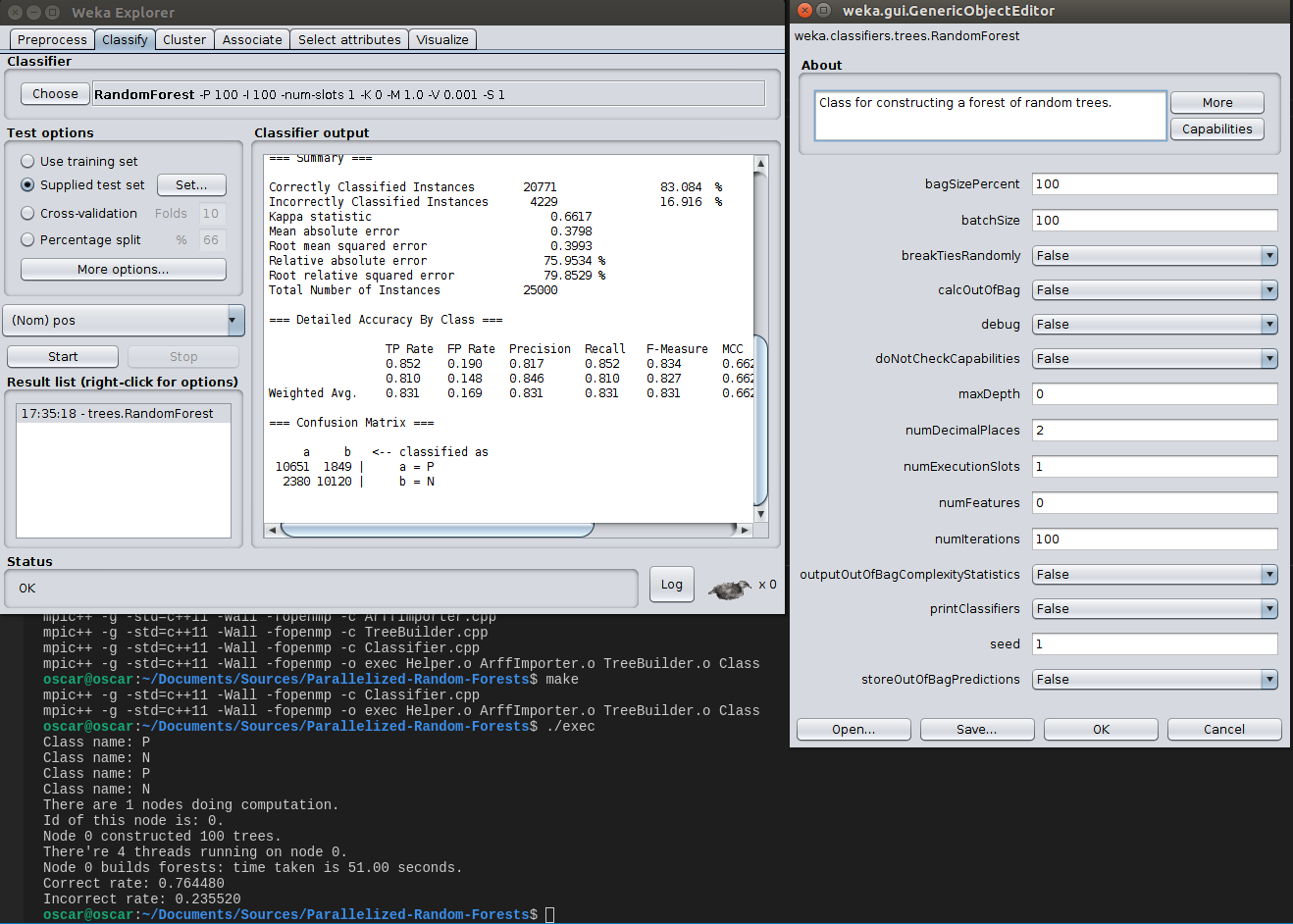
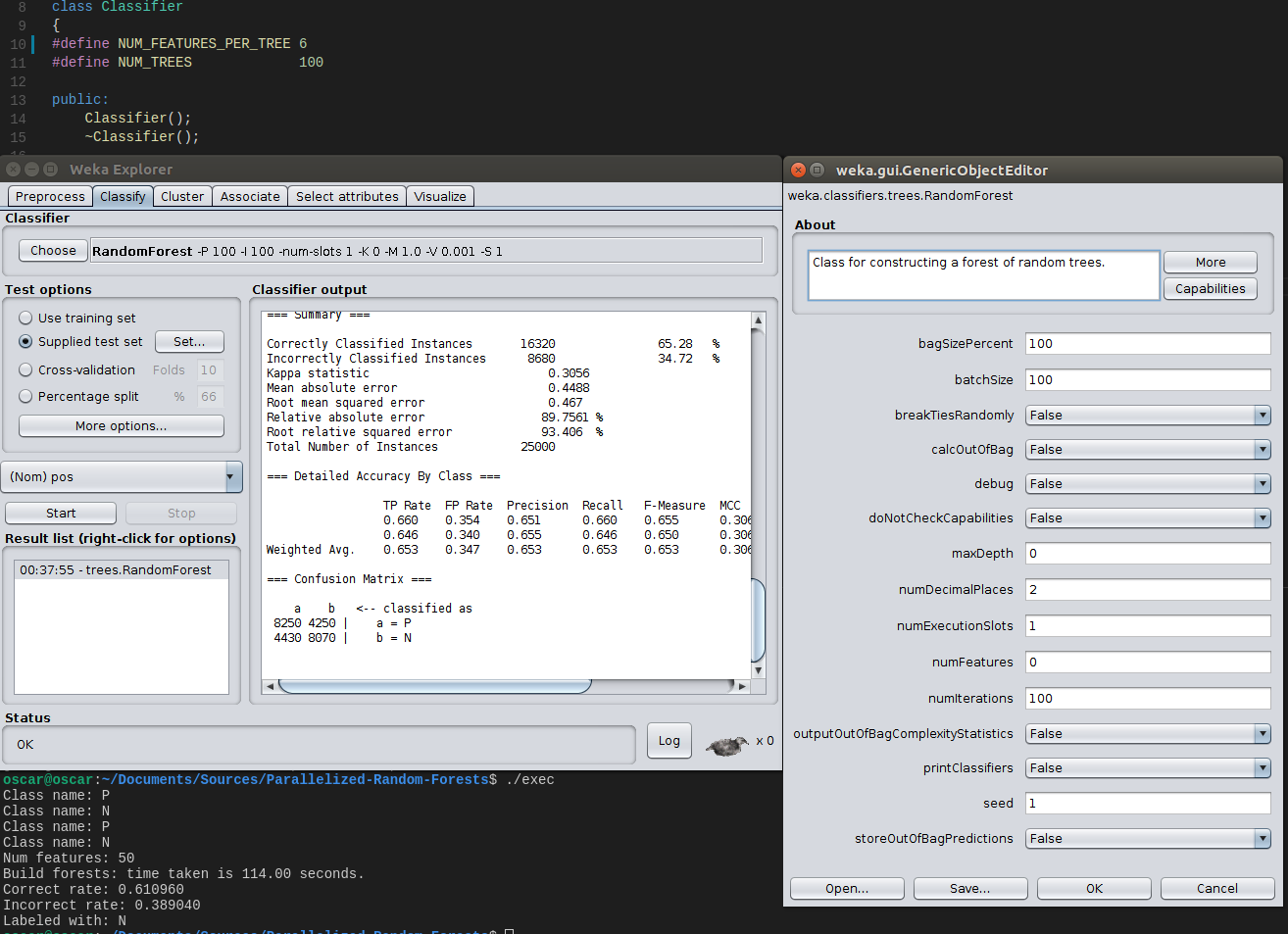
Вот результаты Weka с настройками по умолчанию и мои результаты с теми же настройками (100 деревьев, 10 случайных объектов, рассмотренных во время разделения):
Сначала я подумал, что в моих импортерах данных есть ошибки. Затем я проверил своих импортеров и сравнил их с импортерами python arff и обнаружил, что они работают правильно.
Затем я проверил исходный код weka RF:
http://grepcode.com/file/repo1.maven.org/maven2/nz.ac.waikato.cms.weka/weka-dev/3.7.5/weka/classifiers/trees/RandomForest.java
и тщательно сравнивал с моим более одного раза, чтобы убедиться, что реализации были одинаковыми. И все же я не смог найти причину, по которой все еще оставалась разница в 5%.
Вот ссылка на мою реализацию:
https://github.com/YSZhuoyang/Parallelized-Random-Forests/tree/randomforests
Более конкретно, основная часть алгоритма обучения может быть найдена в «TreeBuilder.cpp» и «TreeBuilder.h».
Обновлено:
Я протестировал 10 данных о функциях и 50 данных о функциях по отдельности, все результаты, полученные моей реализацией, были ниже, чем у реализации weka.
10 функций (100 деревьев, 4 особенности, которые нужно учитывать при разделении):
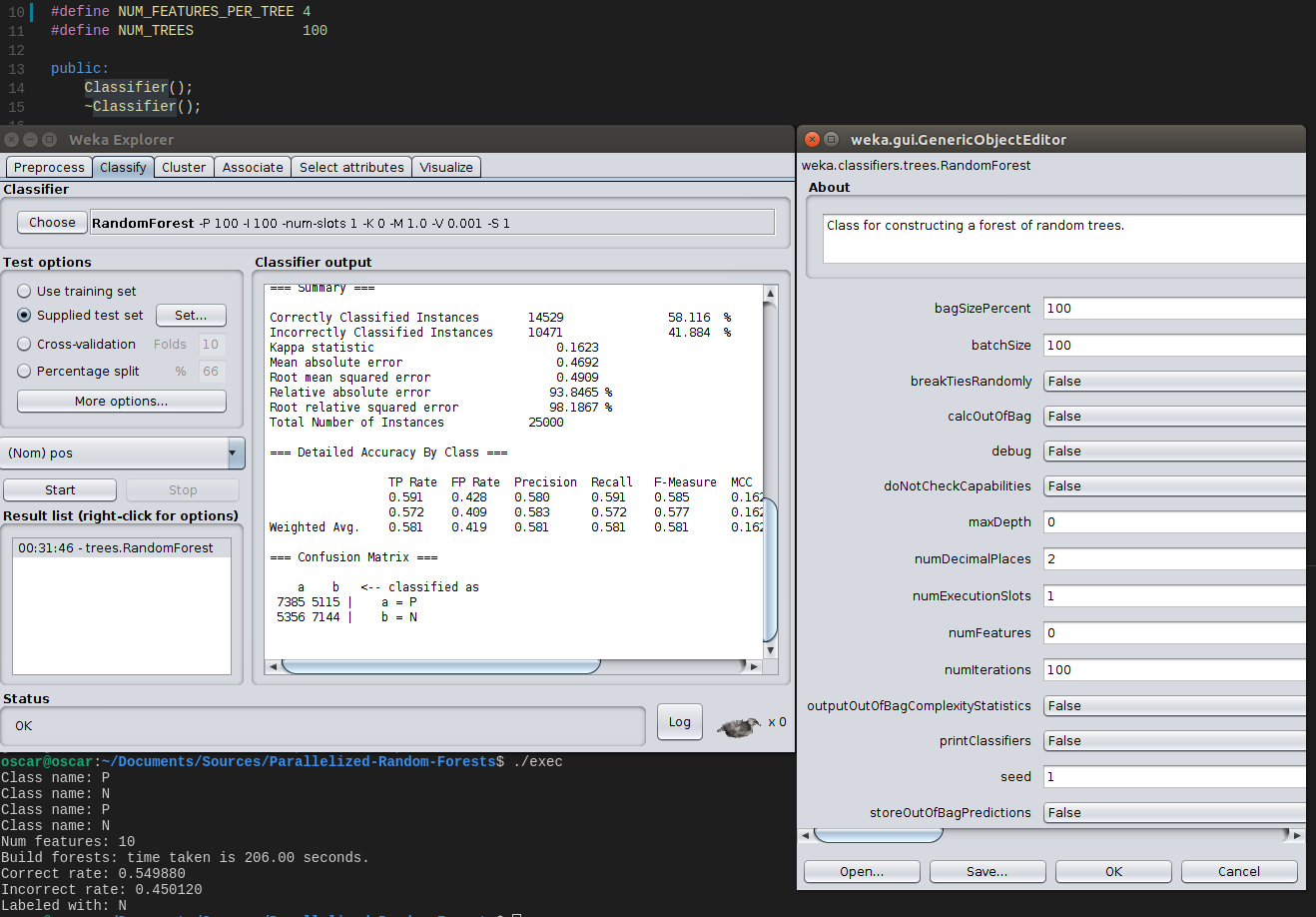
50 функций (100 деревьев, 6 функций, которые нужно учитывать при разделении):
Чтобы немного упорядочить результаты и сделать их более убедительными с точки зрения вариаций, связанных с рандомизацией, я сгруппировал их в следующую таблицу (всего 50 признаков, 6 случайных признаков, рассмотренных во время разделения, оба случайных начальных числа были установлены на 1):
------------------------------------------------------------
| num total features | num trees | weka result | my result |
| 50 | 1 | 55.61 | 52.34 |
| 50 | 5 | 59.08 | 54.35 |
| 50 | 10 | 60.07 | 55.43 |
| 50 | 20 | 62.54 | 57.20 |
| 50 | 50 | 64.14 | 59.56 |
| 50 | 100 | 65.28 | 61.09 |
------------------------------------------------------------
который показал, что это не было связано с рандомизацией.
Решено:
Я использовал набор данных диабета, предоставленный weka, который имеет только 8 функций (следуя предложению @ alexeykuzmin0), и протестировал его на случайном дереве на weka, учитывая все особенности во время разделения. Затем я визуализировал дерево и сравнил его с моим деревом, и обнаружил, что точка разделения, выбранная на корневом узле, отличается от моей, что показалось мне неверным. Наконец, я выяснил, что произошла ошибка типа, приведшая значение типа double к типу int, что привело к неточным результатам.
Кусок кода:
// Compute entropy of children
for (const vector<unsigned int>& group : groups)
{
double entropyChild = ComputeEntropy( group );
// Before being corrected
// unsigned int numChildren = group.size();
// infoGain -= numChildren / numInstances * entropyChild;
// Corrected
double numChildren = group.size();
infoGain -= numChildren / (double) numInstances * entropyChild;
}
Вот обновленная версия сравнения моего и weka:
------------------------------------------------------------
| num total features | num trees | weka result | my result |
| 50 | 1 | 55.61 | 55.34 |
| 50 | 5 | 59.08 | 58.73 |
| 50 | 10 | 60.07 | 60.86 |
| 50 | 20 | 62.54 | 62.97 |
| 50 | 50 | 64.14 | 64.68 |
| 50 | 100 | 65.28 | 65.35 |
------------------------------------------------------------
Спасибо за все ответы и помощь.
Решение
Две реализации (почти) одного и того же алгоритма обучения будут принципиально отличаться во многих аспектах. Это вносит принципиальное отличие: тот же самый DataSET получит немного отличающиеся результаты от аналогичного процесса машинного обучения высокого уровня.
Если реализация точно такая же, результаты не гарантируются идентичными. Наилучший пример, чтобы показать это, — это случайный лесной класс учащихся, обучающихся машинному обучению:
Случайные леса — это леса Бреймана с сильно рандомизированными деревьями
Обратите внимание на слово Рандомизированное.
Как отмечалось в комментарии выше, даже если ни одно из различий других реализаций не может быть интересным для читателей, сама природа Случайного леса требует рандомизации — как повторно используемого инструмента — чтобы иметь место при обработке.
Тщательное исследование требует использования повторяемых экспериментов, и, таким образом, учащиеся из случайных лесов, как правило, позволяют предоставить явно предоставленное значение seed значение для базового ГСЧ (генератор случайных чисел).
Тестирование же RandomForest .fit() метод на том же DataSET, но с разными seed Предоставленное значение приводит к некоторому отклонению в результирующей (im) -точности, достигнутой в отношении принципиально идентичных повторений процесса. Предоставление того же seed значение должно обеспечивать такие же результаты (если и только если, в случае, если никакой другой процесс, расположенный рядом с хостом, не повреждает промежуточные состояния состояний фабрики ГСЧ, использованной на этапе генерации случайного леса).
Хорошей новостью является то, что это количество основное отклонение уменьшается с примерно> 10% по мере роста ансамбля (чем меньше количество деревьев, тем ниже основная дисперсия, вносимая ГСЧ).
Таким образом, 4–6% вполне доступны для такого рода явлений для РФ.
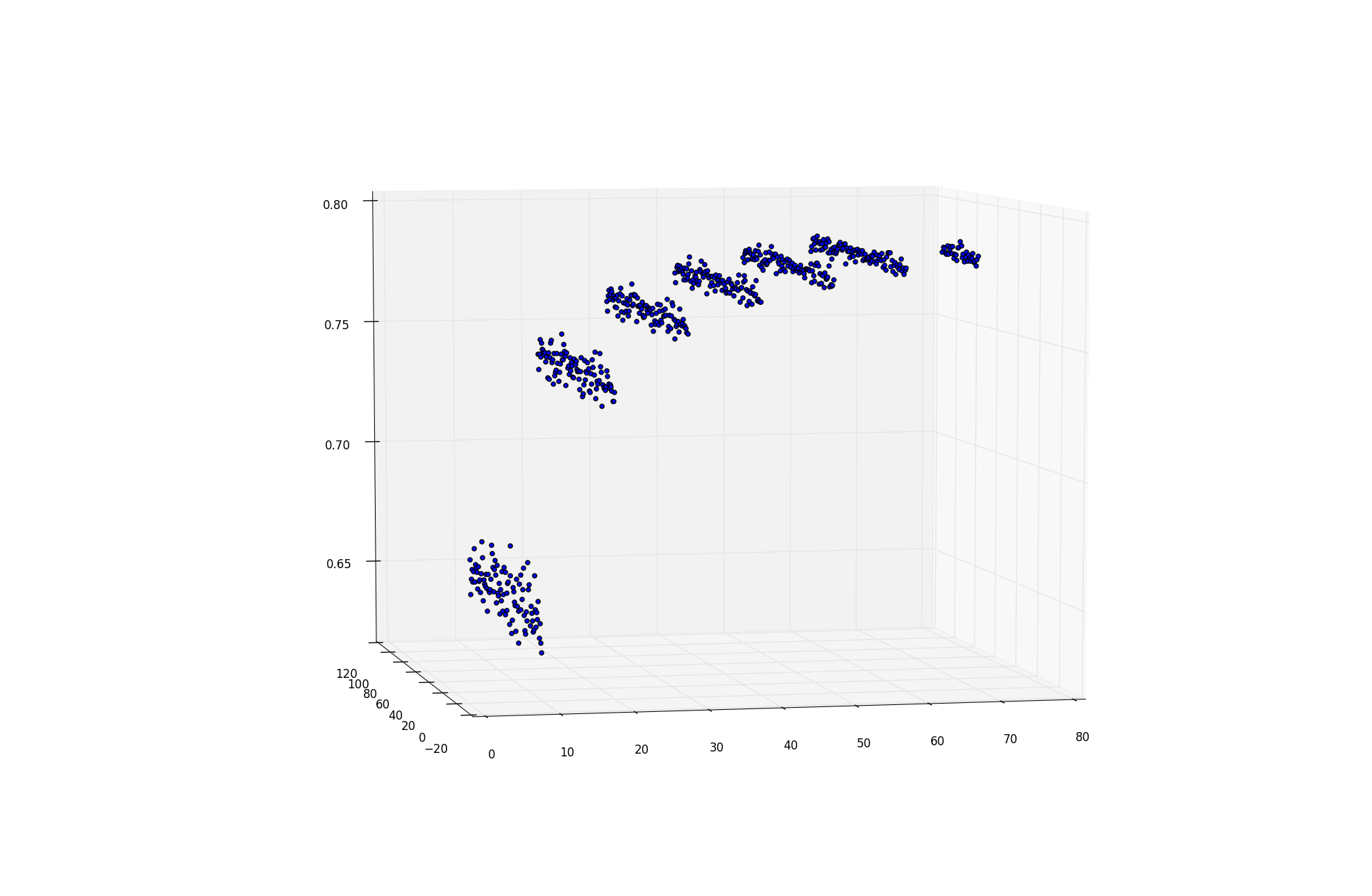
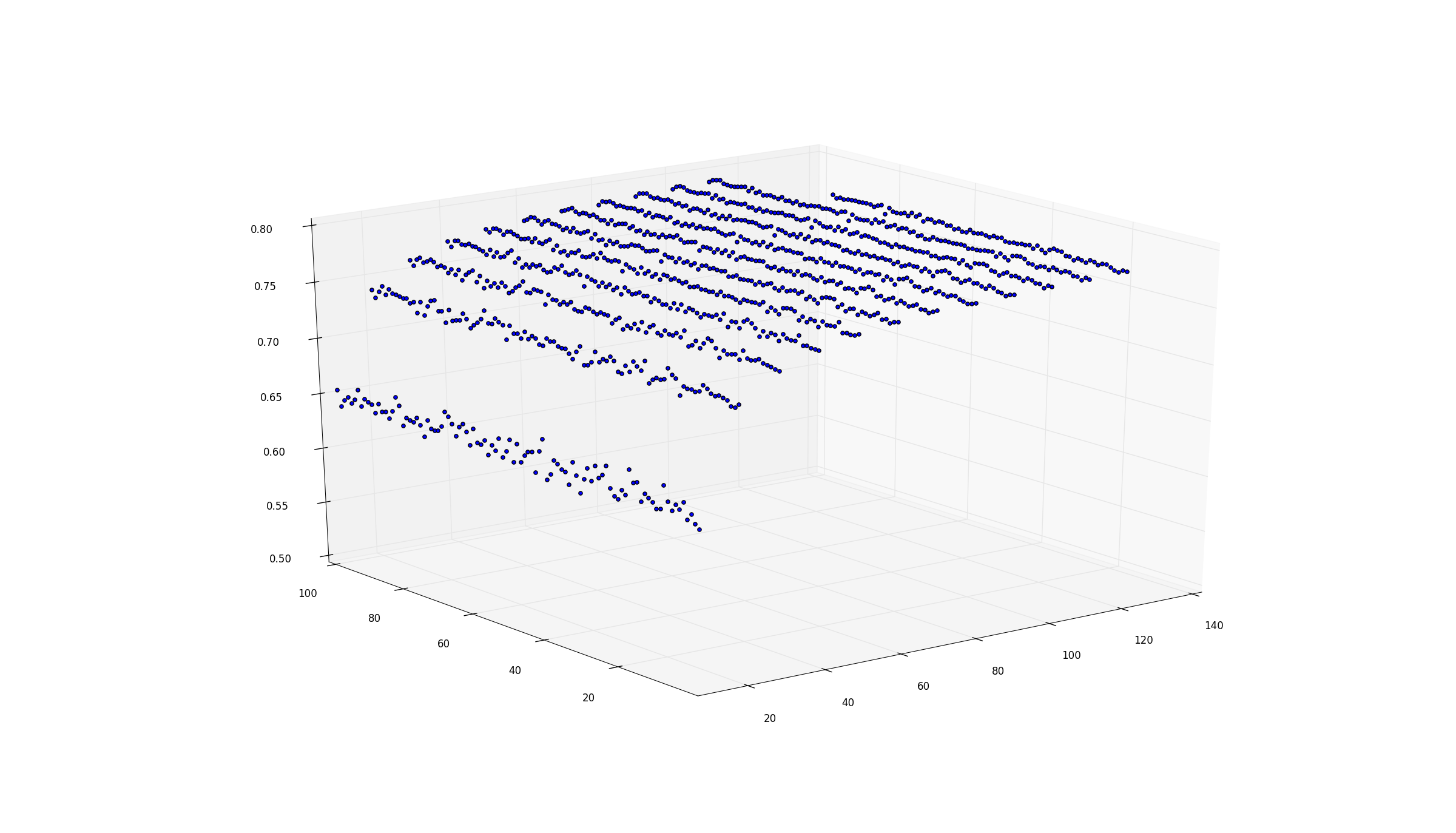
Z-ось показывает повышение прогнозирующей эффективности метода ансамбля «Случайный лес» + уменьшающаяся величина основной дисперсии (введено разными RNG( seed ) ) накладывается на прогнозы.
Ось абсцисс (бежит направо) несет N_trees
Ось ординат (бежит налево) несет seed-ординальное число ~ 100 различных явных seed значения (началось с aBASE, aBASE+1, +2, +3, ..., +99 )
эпилог
Учитывая OP, вы можете повторно протестировать свою собственную реализацию для RNG-seed зависимость путем повторного запуска вашей реализации RF-учащихся на том же DataSET получить количественную оценку этого явления на вашем [ Your-Learner, DataSET, ( Your-RNG, seed ) ] (сейчас) -детерминированная система.
Если вы можете выполнить тот же тест на [ Weka-Learner, DataSET, ( Weka-RNG, seed ) ] сложный, более четкий вид на этот основной пейзаж, который вы получаете.
Другие решения
Других решений пока нет …