Случайно инкрементный подход для вырожденного случая 4 триангуляции Делоне не ведет себя должным образом

Я пытаюсь реализовать алгоритм, приведенный в (1), для получения триангуляции Делоне для набора точек, но я застреваю, когда пытаюсь справиться с вырожденными случаями. Прежде всего, я реализую подход, представленный Гленом Эгучи в «Вычислительной геометрии 6.838» 11 октября 2001 г., поскольку в этой процедуре используется три отправные точки вместо двух, предложенных в книге, и легче выполнять поиск по направленному ациклическому графу, который хранит треугольники. С другой стороны, объяснение, приведенное в книге о том, как обрабатывать точки, принадлежащие дополнительным треугольникам, немного сложно, и я совсем не понимаю.

Проблема в том, что в соответствии с этим подходом в начале процедуры необходимо обрабатывать такой случай, когда в качестве вершин треугольника добавлена ​​любая из ограничивающих точек к исходному набору точек, заданному в результате четырех вырожденных случаев:

Случай 1) Индексы i и j оба являются отрицательными.

• (pi, pj) — край ограничительного треугольника
• (Пи, ПДж) является законным, хотите сохранить края ограничительного треугольника

Случай 2) Индексы i, j, k и l все положительные.

• Это нормальный случай.
• (pi, pj) является недопустимым, если pl лежит внутри окружности (pi, pj, pk)

Случай 3) Ровно один из i, j, k, l отрицателен

• Мы не хотим, чтобы наш ограничивающий треугольник разрушил любые края Делоне.
• Если i или j отрицательны, pipj является недопустимым.
• В противном случае, pipj является законным.

Случай 4) Ровно два из i, j, k, l отрицательны.

• k и l не могут быть оба отрицательными (pk или pl должны быть pr)
• я и j не могут быть оба отрицательными
• Один из i или j и один из k или l должен быть отрицательным
• Если отрицательный индекс i и j меньше отрицательного индекса k и l, (pi, pj) допустимо.
• В противном случае (pi, pj) является незаконным.

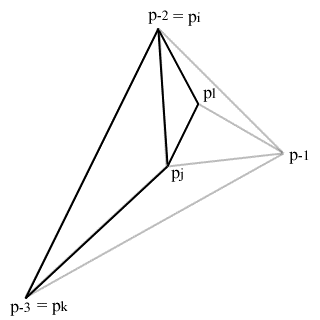
Предлагаемые три отправные точки:

• р-1 = (3М, 0)
• р-2 = (0,3М)
• р-3 = (-3М, -3М)

M = максимальное абсолютное значение любой координаты точки в P

Больше дополнительной помощи можно найти Вот

Рекомендации:

(1) Де Берг М., Ван Кревельд М., Овермарс М., & Schwarzkopf, O. C. (2000). Вычислительная геометрия (стр. 1-17). Springer Berlin Heidelberg.

Я даю вам простые тестовые случаи, которые не работают должным образом, если я добавлю случай 4 в алгоритм. Причина в том, что, если я включу такой случай, то, когда у меня есть только две точки, добавленные из набора точек, нет возможности найти ребро, которое удерживает любую из юридических частей вышеупомянутых дел, после того, как оно обнаружит недопустимое ребро из-за случая 4 Пока я удаляю этот случай из моей реализации, и алгоритм работает, но я предполагаю, что алгоритм не завершен, если я не включу этот случай, потому что это важно для некоторого набора точек. Я все еще работаю в найти это:

3
0 0
4 0
0 4

Первая строка, количество очков. Затем координаты x и y каждой точки на линии. Порядок вставленных точек (это важно, поскольку в этом подходе точки вставляются случайным образом) следующий (0,4) -> (0,0) -> (4,0).

Это функция legalizeEdge, которую я реализовал, закомментированные строки относятся к случаю 4:

/* Take into account that the symbolical points at the bounding triangle
* could be part of the edges to legalize */
void legalizeEdge(point pr, seg s) {
bool ill = 0;
int fn = 0, sn = 0;
pair<int, int> adj = Q[s];
point pl =
contain(nodes[adj.first].t, pr) ?
getPoint(nodes[adj.second].t, s) :
getPoint(nodes[adj.first].t, s);

if (s.first == p_1 || s.first == p_2 || s.first == p_3) {
fn = s.first == p_3 ? -3 : s.first == p_1 ? -1 : -2;
if (s.second == p_1 || s.second == p_2 || s.second == p_3) {
return; // Case 1: is always legal
}
}

if (s.second == p_1 || s.second == p_2 || s.second == p_3) {
fn = s.first == p_3 ? -3 : s.first == p_1 ? -1 : -2;
}

if (pl == p_1 || pl == p_2 || pl == p_3) {
// Case 4: both either(i,j) and l must be negative
/*sn = pl == p_1 ? -3 : pl == p_1 ? -1 : -2;
if(!fn) {
return; // Case 3: is legal only when i or j are not negative
}
else if (fn < sn)
return; // if min(i,j) < l
else
ill = 1;*/
return;
} else if(fn) {
ill = 1; // Case 3 read above
}

if (ill || inCircle(pr, s.first, s.second, pl)) { // is illegal
// Case 2 or illegal Case 3
seg news;
int firstt, secondd;
pair<int, int> nadj;
point pj = s.first, pi = s.second;

// replace s(pj,pi) with s(pr,pl) flip edge!!!

firstt = contain(nodes[adj.first].t,pl) ? adj.first:adj.second;
secondd = firstt == adj.first ? adj.second:adj.first;

Q.erase(s);
news = getSeg(pr,pl);
insTrang(pr, pj, pl), nadj.first = IDX,
nodes[adj.first].son.push_back(IDX), nodes[adj.second].son.push_back(
IDX);

updateMap(pl,pj,firstt);
updateMap(pr,pj,secondd);

insTrang(pr, pl, pi), nadj.second = IDX,
nodes[adj.first].son.push_back(IDX), nodes[adj.second].son.push_back(
IDX);

updateMap(pi,pr,secondd);
updateMap(pi,pl,firstt);

Q[news] = nadj;

seg sa = getSeg(pi,pl);
legalizeEdge(pr, sa);

seg sb = getSeg(pj,pl);
legalizeEdge(pr, sb);
}
}

Заранее спасибо.