Скорость квадратичной кривой
Я пишу 2D-игру, и у меня есть птицы в пространстве камеры. Я хочу заставить их летать. Итак, я генерирую 3 ~ случайные точки. Первый левый верхний край, второй: средний нижний, третий: правый верхний.
В результате я повернул треугольник на 180 градусов.
Для перемещения птицы по пути кривой у меня есть t-параметр, который увеличивается в каждом кадре (цикл рендеринга) на некоторую дельту.
Проблема в том, что у птиц разные кривые разной скорости. Если треугольник «широкий» (1) они медленнее, если они растянуты по Y-координате (2), скорость очень быстрая.
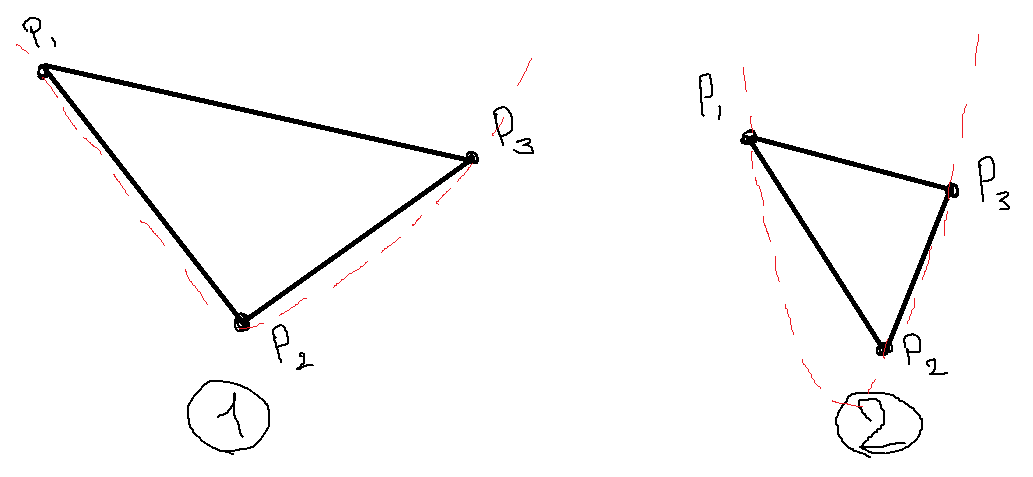
Но я хочу сделать скорость равной на разных поворотах. Логично, что я должен изменить delta который добавляется каждый кадр для каждой кривой.
Я пытался решить это так:
Найдите длину кривой, суммируя длину 2 векторов: P1P2 а также P2P3,
Чем я определил скорость для 1 виртуального метра на кадр. Маленький псевдокод:
float pixelsInMeter = 92.f; // One virtual meter equals to this number of pixels
float length = len(P1P2) + len(P2P3)
float speed = 0.0003f; // m/frame
// (length * speed) / etalon_length
float speedForTheCurve = toPixels( (toMeters(length) * speed) / 1.f);
// ...
// Each frame code:
t += speedForTheCurve;
Vector2 newPos = BezierQuadratic(t, P1, P2, P3);
Но птицы в любом случае имеют разную скорость. В чем дело? Или, может быть, есть лучший способ.
Решение
Используемая вами функция Безье является параметризованной функцией с границами [0 … 1]. Вы гадите с размером шага, поэтому вы получаете сумасшедшие скорости. Вообще говоря, расстояние d является зависимой переменной в уравнении, которое говорит мне, что их скорости будут отличаться в зависимости от длины кривой.
Поскольку скорость является вашей зависимой переменной, мы собираемся векторизовать вашу функцию, вычисляя размер шага.
Проверьте этот псевдокод:
P1 = (x1, y1)
P2 = (x2, y2)
P3 = (x3, y3)
int vec[100][2]
int getPoint(int p1, int p2, float stepSize) {
return p1 + (p2 - p1)*stepSize;
}
for (float i = 0.0; i < 1.0; i += 0.01 ) {
int newX = getPoint(getPoint(x1, x2, i), getPoint(x2, x3, i), i);
int newY = getPoint(getPoint(y1, y2, i), getPoint(y2, y3, i), i);
vec[iter++][0] = newX;
vec[iter][1] = newY;
}
Вы можете получить значения дельты, выполнив первое различие, но я не думаю, что это необходимо. Пока вы перемещаете всех птиц на соответствующее расстояние, основанное на шаг итерации, они все будут перемещаться на разные расстояния, но они будут начинать и заканчивать свои траектории одинаково.
Из вашего уравнения мы можем вычислить размер шага пикселя:
int pixelsToMove = toMeter(sqrt((x2 - x1)^2 + (y2 - y1)^2))/pixelsInMeter;
Что даст вам соответствующее количество пикселей для перемещения птицы. Таким образом, они все будут двигаться с разными размерами шагов, но их скорости будут разными. Имеет ли это смысл?
Или попробуйте что-то вроде этого (гораздо сложнее):
- Получите фактическую квадратичную функцию трех выбранных вами точек.
- Интегрировать квадратичный между двумя
xyпрямоугольная координата - Преобразовать вычисленную длину в пиксели или что вы используете
- Получите зависимую переменную скорость, чтобы все кривые заканчивались одновременно.
Начнем с квадратичного:
y = Ax^2 + Bx + C где A != 0, так как у вас есть три точки, вам нужно три уравнения. Используя алгебру, вы можете решить для констант:
A = (y3 - y2)/((x3 - x2)(x3 - x1)) - (y1 - y2)/((x1 - x2)(x3 - x1))
B = (y1 - y2 + A(x2^2 - x1^2))/(x1 - x2)
C = y1 - Ax1^2 - Bx1
Затем вы можете использовать формулу выше, чтобы получить длину дуги замкнутой формы. Проверьте этот веб-сайт, wolfram будет интегрировать его для вас, и вам просто нужно ввести его:
Решение в закрытой форме для квадратичной интеграции
Теперь, когда вы вычислили длину дуги, преобразуйте actualArcLength на скорость или любую единицу, которую вы используете:
float speedForTheCurve = toPixels( (toMeters(actualArcLength) * speed) / 1.f);
Другие решения
Других решений пока нет …
