Самый большой номер & lt; Икс?

В C ++, скажем, у меня есть номер x типа T который может быть целочисленным или с плавающей точкой. Я хочу найти наибольшее число y типа T для которого y < x держит. Решение должно быть шаблонным, чтобы прозрачно работать как с целыми числами, так и с числами с плавающей запятой. Вы можете игнорировать крайний случай, когда x уже наименьшее число, которое может быть представлено в T,

Возможный случай использования: Этот вопрос был помечен как слишком локализованный, поэтому я хотел бы привести пример использования, который я считаю более общим. Обратите внимание, что я не являюсь первоначальным автором ОП.

Рассмотрим эту структуру:

struct lower_bound {
lower_bound(double value, bool open) : value(open? value+0.1 : value) {}
double value;
bool operator()(double x) { return x >= value; }
};

Этот класс имитирует нижнюю границу, которая может быть как открытой, так и закрытой. Конечно, в реальной (каламбурной) жизни мы не можем этого сделать. Поток невозможно (или, по крайней мере, довольно сложно) рассчитать для S быть всеми действительными числами.

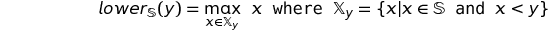
Однако когда S это множество чисел с плавающей запятой, это очень правильный принцип, так как мы имеем дело с по существу счетным множеством; и тогда нет такой вещи как открытая или закрытая граница. То есть> = может быть определено в терминах> как сделано в классе lower_bound.

Для простоты кода я использовал +0.1 для имитации открытой нижней границы. Конечно, 0,1 — это грубое значение, так как могут быть значения z, такие что значение < Z <= значение + 0,1 или значение + 0,1 == значение в представлении с плавающей запятой. Следовательно, ответ @ brett-hale очень полезен 🙂

Вы можете подумать о другом более простом решении:

struct lower_bound {
lower_bound(double value, bool open) : open(open), value(value) {}
bool open;
double value;
bool operator()(double x) { return (open ? x > value : x>=value); }

};

Однако это менее эффективно, так как sizeof (Lower_bound) больше, и operator () должен выполнить более сложный оператор. Первая реализация действительно эффективна и может быть реализована просто как двойная структура вместо структуры. Технически, единственной причиной для использования второй реализации является то, что вы предполагаете, что double является непрерывным, тогда как это не так, и я предполагаю, что его не будет нигде в обозримом будущем.

Я надеюсь, что я создал и объяснил действительный вариант использования, и что я не обидел оригинального автора.