Рекомендации по методике интеграции функций Бесселя в переполнение стека

Мне нужно интегрировать колебательную функцию такого рода:

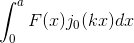
где у меня есть функция Бесселя, которая колеблется, в то время как F не очень колебательный. Я ищу самый точный / точный способ сделать это в C ++. Надеюсь, это должна быть уже существующая реализация, которую я могу использовать, например, через библиотеку и т. Д.

Библиотека GSL может быть вариантом, но, пожалуйста, даже в этом случае, не могли бы вы порекомендовать мне, какая из многих доступных подпрограмм наиболее полезна для меня?

РЕДАКТИРОВАТЬ:
Я знаю о наличии этого
возможно повторяющийся вопрос

но я не вижу четкого ответа там. Кроме того, библиотека на Фортране не подойдет мне, если только для нее нет какой-то обертки.

0

bessel-functions c++numerical-methods

Решение

Другие решения

Других решений пока нет …

Источник

Accepted Answer

В прошлый раз, когда мне приходилось иметь дело с такими вещами, было просто сделать простую интеграцию интервалов, определяемых переходами через ноль. Это в большинстве случаев относительно стабильно, и если подынтегральная функция приближается к нулю, достаточно быстро, что легко сделать.

В качестве отправной точки для игры я включил немного кода. Конечно, вам нужно работать над обнаружением сходимости и проверкой ошибок. Это не рабочий код, но я подумал, что он может послужить отправной точкой для вас. Его использование GSL.

На моем iMac этот код занимает около 2 мкс на итерацию. Он не станет быстрее при включении таблицы с жестким кодом для интервалов.

Надеюсь, это вам пригодится.

#include <iostream>
#include <vector>
#include <gsl/gsl_sf_bessel.h>
#include <gsl/gsl_integration.h>
#include <gsl/gsl_sf.h>double f (double x, void * params) {
double y = 1.0 / (1.0 + x) * gsl_sf_bessel_J0 (x);
return y;
}

int main(int argc, const char * argv[]) {

double sum = 0;
double delta = 0.00001;
int max_steps = 1000;
gsl_integration_workspace * w = gsl_integration_workspace_alloc (max_steps);

gsl_function F;
F.function = &f;
F.params = 0;

double result, error;
double a,b;
for(int n=0; n < max_steps; n++)
{
if(n==0)
{
a = 0.0;
b = gsl_sf_bessel_zero_J0(1);
}
else
{
a = n;
b = gsl_sf_bessel_zero_J0(n+1);
}
gsl_integration_qag (&F,  // function
besselj0_intervals[n],   // from
besselj0_intervals[n+1],   // to
0,   // eps absolute
1e-4,// eps relative
max_steps,
GSL_INTEG_GAUSS15,
w,
&result,
&error);
sum += result;

std::cout << n << " " << result << " " << sum << "\n";

if(abs(result) < delta)
break;
}
return 0;
}

1