реализация закона де Моргана с использованием C / Stack Overflow
-
выражение 1: (А и В или (не С))
-
выражение 2: не ((не A) или (не B) и C)
Я хочу изменить выражение 2 на expression1. Таким образом, выражение может быть выражено в виде дерева, как на рисунке ниже. Это означает, что операция «не» может существовать только в конечном узле.
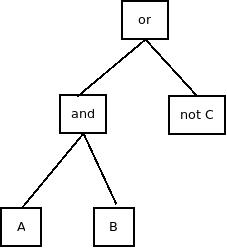
Преобразование основано на Закон де Моргана.
И вот мой вопрос:
Существует ли библиотека C / C ++ для реализации этой функции? Я не знаю много о библиотеке C / C ++. я искал GMP а также http://mathworld.wolfram.com/ но не нашел решения.
Спасибо!
Решение
Правило простое, когда вы думаете об этом рекурсивно:
not (X and Y)==>(not X) or (not Y)not (X or Y)==>(not X) and (not Y)
так в C ++:
struct Node {
virtual ~Node() {};
virtual Node *copy() = 0;
virtual Node *negation() = 0;
private:
// Taboo
Node(const Node&);
Node& operator=(const Node&);
};
struct AndNode : Node {
Node *left, *right;
AndNode(Node *left, Node *right) : left(left), right(right) {}
~AndNode() { delete left; delete right; }
Node *copy() { return new AndNode(left->copy(), right->copy()); }
Node *negation();
};
struct OrNode : Node {
Node *left, *right;
OrNode(Node *left, Node *right) : left(left), right(right) {}
~OrNode() { delete left; delete right; }
Node *copy() { return new OrNode(left->copy(), right->copy()); }
Node *negation();
};
struct NotNode : Node {
Node *x;
NotNode(Node *x) : x(x) {}
~NotNode() { delete x; }
Node *copy() { return new NotNode(x->copy()); }
Node *negation();
};
struct VarNode : Node {
std::string var;
VarNode(const std::string& var) : var(var) {}
Node *copy() { return new VarNode(var); }
};
negation код для and а также or Операция просто применяет закон Де Моргана, таким образом, «отталкивая» отрицание вниз по дереву
Node *AndNode::negation() {
return new OrNode(left->negation(), right->negation());
}
Node *OrNode::negation() {
return new AndNode(left->negation(), right->negation());
}
Отрицание отрицания вместо этого делает упрощение elision
Node *NotNode::negation() {
return x->copy();
}
Только конечный узел фактически обернут в операцию отрицания
Node *VarNode::negation() {
return new NotNode(this->copy());
}
Как видите, закон Моргана состоит из двух строк, а все остальное — как представить дерево выражений в C ++. Нет смысла иметь библиотеку для реализации преобразования Де Моргана только потому, что если у вас есть представление, это абсолютно тривиально.
Реализация с обертками, чтобы иметь возможность работать с различными представлениями дерева, была бы на 99% стандартным шаблоном и интерфейсным кодом для реализации двухстрочного (полная ерунда).
Просто реализуйте это напрямую с любым представлением дерева.
Другие решения
Других решений пока нет …
