Реализация возврата в Knight’s tour с выбором массива шагов
Таким образом, я придумал эту реализацию для решения тура рыцарей для шахматной доски 8 * 8.
Но похоже, что это занимает много времени (так долго, что я должен остановить это). Но если я заменю dx, массивы dy на те, что написаны в комментариях, и программа работает как по волшебству и выдает результат. Говорят, что он разумно выбирает массив, так что брутфорс-альго везет быстро найти решение.
Но как создать этот массив в первую очередь, этот массив (dx, dy), который я получил из другого кода. Так может кто-нибудь объяснить мне, почему этот код работает с этими массивами (в комментариях), а не с моим.
#include <cstdio>
using namespace std;
int dx[8] = { 1, 1, 2, 2, -1, -1, -2, -2};
int dy[8] = { 2, -2, 1, -1, 2, -2, 1, -1};
//int dx[8] = { 2, 1, -1, -2, -2, -1, 1, 2 };
//int dy[8] = { 1, 2, 2, 1, -1, -2, -2, -1 };
bool solve(bool arr[8][8],int x,int y,int moves){
if(moves==0)return true;
if(x<0 || y<0 || x>7 || y>7 || arr[x][y])return false;
arr[x][y]=1;
for(int i=0;i<8;i++)
if(solve(arr,x+dx[i],y+dy[i],moves-1)){
printf(" (%d,%d) ",x,y);
return 1;
}
arr[x][y]=0;
return false;
}
int main()
{
bool arr[8][8];
for(int i=0;i<8;i++) for(int j=0;j<8;j++) arr[i][j]=0;
solve(arr,0,0,64);
puts("");
}
Решение
Резюме
Причина закомментированная dx/dy Массив работает лучше, чем ваш первоначальный массив, потому что он выполняет поиск в глубину для решения в другом порядке — порядке, который был выбран с учетом конкретного решения и который поэтому может найти это решение относительно быстро.
подробности
Поиск в глубину начинается с корня дерева и исследует каждый путь к листу. Например, поиск в глубине этого дерева сначала изучит путь, который посещает только a узлы (a -> a -> a) тогда бы немного откатился назад и осмотрел a -> a -> b, затем a -> a -> c, так далее.
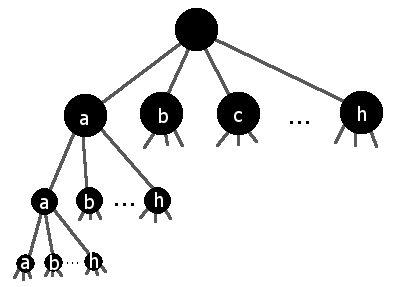
Это может занять много времени, если дерево большое и нет решений, которые начинаются с посещения a, потому что ты приходится тратить много времени исследуя все пути, которые начинаются с a прежде чем вы сможете перейти к лучшим путям.
Если вы знаете, что есть хорошее решение, которое начинается с dВы можете немного ускорить процесс, переупорядочив узлы своего дерева так, чтобы вы начали с изучения путей, начинающихся с d:
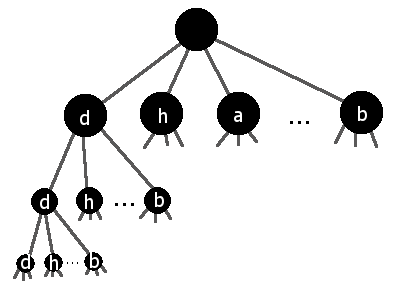
Сразу же вы удалили 7/8 работы, которую должна выполнять ваша программа, потому что вам никогда не придется искать пути, начинающиеся с чего-то другого, кроме d! Выбрав хороший порядок для остальных узлов, вы можете получить аналогичные ускорения.
Вы можете увидеть, что это происходит, если вы посмотрите на вывод вашей программы:
(0,7) (1,5) (3,4) (1,3) (0,1) (2,0) (4,1) (6,0) (7,2) (5,3) (7,4)
(6,2) (7,0) (5,1) (4,3) (3,1) (5,0) (7,1) (5,2) (7,3) (6,1) (4,0)
(3,2) (4,4) (2,3) (0,2) (1,0) (2,2) (3,0) (1,1) (0,3) (2,4) (1,2)
(0,4) (1,6) (3,7) (2,5) (3,3) (5,4) (6,6) (4,5) (6,4) (7,6) (5,5)
(4,7) (2,6) (0,5) (1,7) (3,6) (5,7) (6,5) (7,7) (5,6) (3,5) (1,4)
(0,6) (2,7) (4,6) (6,7) (7,5) (6,3) (4,2) (2,1) (0,0)
Первый ход (чтение снизу) от (0,0) в (2,1)что соответствует dx=2 а также dy=1 — и конечно же, в закомментированном dx/dy список, это первая возможность, которая рассматривается. На самом деле, первые три хода этого решения используют dx=2 а также dy=1что эффективно означает вам нужно только поискать маленькое маленькое поддерево вместо всего этого.
Другие решения
В шахматах есть восемь действительных ходов коня:
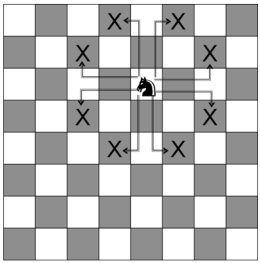
Два массива перечисляют эти восемь ходов.
Две версии кода пробуют ходы в разном порядке. Случается, что одна версия находит правильное решение гораздо быстрее, чем другая.
Это все, что нужно сделать.
