реализация растеризации программного обеспечения ускоряет идеи

float cross(Vec2f const &edge1, Vec2f const &edge2)
{
return edge1[0] * edge2[1] - edge1[1] * edge2[0];
}

bool caculateBarycentricWeights(float invDoubleTriArea, float doubleTriArea, Vec2f const (&edgesFromTo01_12_20)[3], Vec2f const (&vertex)[3], Vec2f const &point, float(&outWeight)[3])
{
outWeight[0] = cross(point - vertex[2], edgesFromTo01_12_20[1]);
outWeight[1] = cross(point - vertex[0], edgesFromTo01_12_20[2]);
outWeight[2] = cross(point - vertex[1], edgesFromTo01_12_20[0]);

if (outWeight[0] >= 0.0f &&  outWeight[1] >= 0.0f &&  outWeight[2] >= 0.0f
&& outWeight[0] + outWeight[1] + outWeight[2] <= doubleTriArea * 1.000001f)
{
outWeight[0] *= invDoubleTriArea;
outWeight[1] *= invDoubleTriArea;
outWeight[2] *= invDoubleTriArea;

return true;
}
else
{
return false;
}
}

void rasterize(Vec3f const &vertex0, Vec3f const &vertex1, Vec3f const &vertex2, vector<Vec3f> &dstBuffer)
{
Vec2f const edgesFromTo01_12_20[3] =
{
Vec2f(vertex1[0] - vertex0[0], vertex1[1] - vertex0[1]),
Vec2f(vertex2[0] - vertex1[0], vertex2[1] - vertex1[1]),
Vec2f(vertex0[0] - vertex2[0], vertex0[1] - vertex2[1])
};

//in viewport space up and down is switched, thats why '-'
float const doubleTriangleArea = -cross(edgesFromTo01_12_20[0], edgesFromTo01_12_20[1]);
float const invDoubleTriangleArea = 1.0f / doubleTriangleArea;float weight[3];

float invZ[3] = { 1.0f / vertex0[2], 1.0f / vertex1[2], 1.0f / vertex2[2] };

Vec2f p(vertex0[0], vertex0[1]);

Vec2f vPos[3] = {
Vec2f(vertex0[0], vertex0[1]),
Vec2f(vertex1[0], vertex1[1]),
Vec2f(vertex2[0], vertex2[1])
};

const size_t RES_X = 1024;
const size_t RES_Y = 768;

for (size_t y = 0; y < RES_Y; ++y)
{
p[1] = y;

for (size_t x = 0; x < RES_X; ++x)
{
p[0] = x;

if (caculateBarycentricWeights(invDoubleTriangleArea, doubleTriangleArea, edgesFromTo01_12_20, vPos, p, weight))
{
//interpolate values
float z = 1.0f / (weight[0] * invZ[0] + weight[1] * invZ[1] + weight[2] * invZ[2]);
dstBuffer[y * RES_X + x] = ((vertex0 * (weight[0] * invZ[0])) + (vertex1 * (weight[1] * invZ[1])) + (vertex2 * (weight[2] * invZ[2]))) * z;

}
}
}
}int main(int argc, char *argv[])
{
vector<Vec3f> buffer;
buffer.resize(1024 * 768);

high_resolution_clock::time_point start = high_resolution_clock::now();
size_t fps = 0;

while (true)
{

static Vec3f v0 = { -2000.0f, -2000.0, 10.0 };
static Vec3f v1 = { 2000.0f, -2000.0, 10.0 };
static Vec3f v2 = { 0.0f, 2000.0, 10.0 };

rasterize(v0, v2, v1, buffer);
++fps;

high_resolution_clock::time_point now = high_resolution_clock::now();
auto timeDiff = duration_cast<microseconds>(now - start).count();

static const long oneSecond = 1000000;
if (timeDiff >= oneSecond)
{

cout << fps << " ";

fps = 0;
start = now;
}

}return 0;
}

Я считаю, что я должен быть в состоянии победить 130 FPS.

…даже Quake2 работал быстрее

Я должен признать, что я получил вдохновение от OpenGL — напоминает несколько его частей (по крайней мере, насколько я считаю, что это может работать) и с некоторыми упрощениями.

Я должен также признать, что я не понял, что именно caculateBarycentricWeights() функция хороша для.

Однако я основал свою реализацию на следующей концепции:

1. растеризатор должен работать в пространстве экрана

2. 3D вершины должны быть преобразованы в пространство экрана перед растеризацией

3. Внутренний растровый цикл должен быть как можно более простым — ответвления (т.е. if и сложная функция) в самом внутреннем цикле, безусловно, контрпродуктивны.

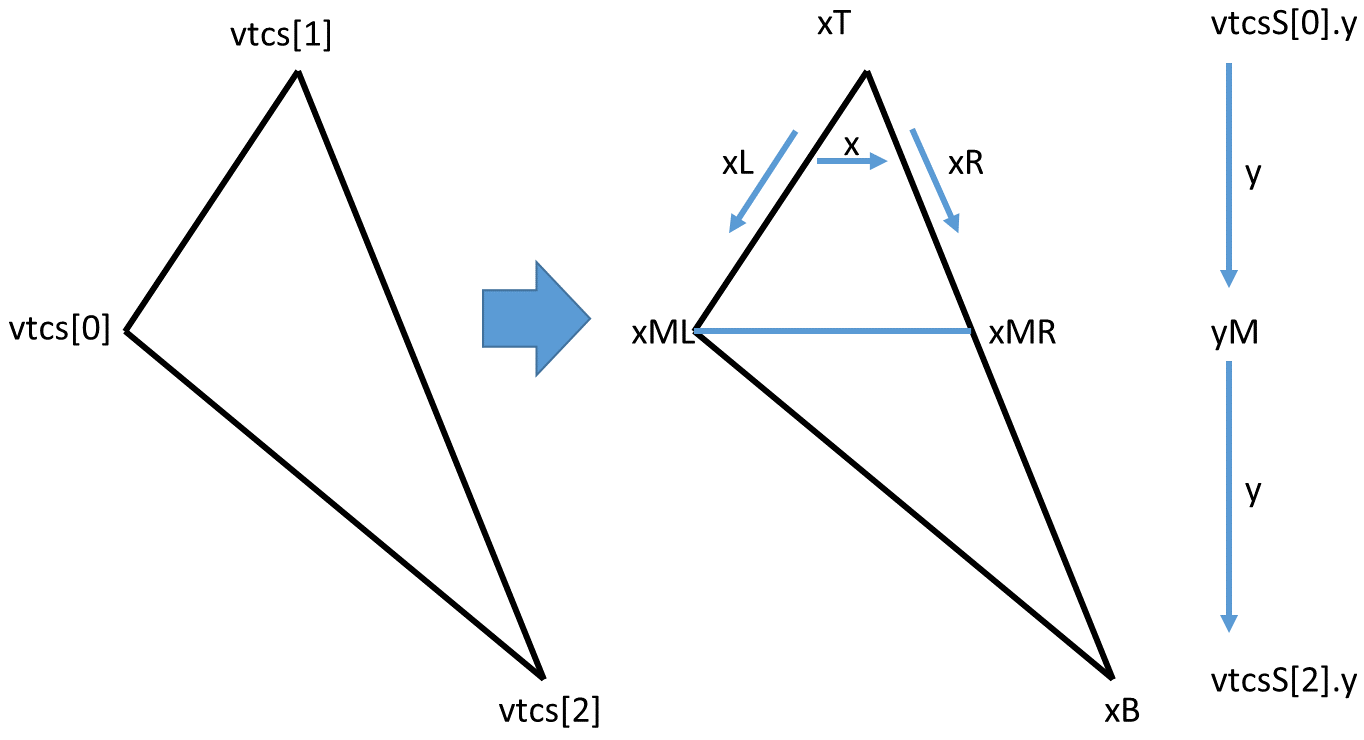
Следовательно, я сделал новый rasterize() функция. Тем самым я считал, что rasterize() должен заполнить горизонтальные линии экрана. Для этого я сортирую 3 вершины треугольника по их y компоненты. (Обратите внимание, что вершины должны быть предварительно преобразованы в пространство экрана.) В обычном случае это позволяет разрезать треугольник по горизонтали на две части:

• верхний с вершиной выше горизонтального основания
• нижняя с пиком ниже горизонтального основания.

Исходный код приведен ниже, но эскиз может помочь сделать все интерполяции немного более понятными:

Чтобы преобразовать vtcs заранее для скрининга пространства я использовал две матрицы:

const Mat4x4f matProj(InitScale, 1.0f / Width, 1.0f / Height, 1.0f);
const Mat4x4f matScreen
= Mat4x4f(InitScale, 0.5f * Width, 0.5f * Height, 1.0f)
* Mat4x4f(InitTrans, Vec3f(1.0f, 1.0f, 0.0f));
const Mat4x4f mat = matScreen * matProj /* * matView * matModel */;

где

• matProj матрица проекции для масштабирования координат модели для обрезки пространства
• matScreen отвечает за преобразование пространства клипа в пространство экрана.

Клип пространство — это пространство, где видимая часть находится в диапазоне [-1, 1] для x, y и z.

Пространство экрана имеет диапазоны [0, ширина) и [0, высота), где я использовал width = 1024 а также height = 768 согласно требованию ОП.

Когда я создаю программы OpenGL, это (своего рода) раздражающая традиция, которую я каждый раз начинаю с синего экрана (так как синий — мой любимый чистый цвет). Это в основном вызвано путаницей некоторых операций с матрицами, за которыми следуют попытки найти и исправить эти операции. Поэтому я попытался визуализировать результат растеризации, чтобы убедиться, что мой тест не слишком увлечен, потому что просто любая часть треугольника находится вне поля зрения и, следовательно, отсечена:

Я бы посчитал это наглядным доказательством. Чтобы добиться этого, я обернул образец растеризатора в простое приложение Qt, где FBO данные хранятся в QImage который в свою очередь применяется к QPixmap отображается с QLabel, Получив это, я подумал, что было бы неплохо добавить какую-то простую анимацию, изменяя матрицу вида модели с течением времени. Итак, я получил следующий образец:

#include <cstdint>
#include <algorithm>
#include <chrono>
#include <iostream>
#include <vector>

#include "linmath.h"
typedef unsigned uint;
typedef std::uint32_t uint32;

const int Width = 1024, Height = 768;

class FBO {
public:
const int width, height;
private:
std::vector<uint32> _rgba; // pixel buffer
public:
FBO(int width, int height):
width(width), height(height),
_rgba(width * height, 0)
{ }
~FBO() = default;
FBO(const FBO&) = delete;
FBO& operator=(const FBO&) = delete;

void clear(uint32 rgba) { std::fill(_rgba.begin(), _rgba.end(), rgba); }
void set(int x, int y, uint32 rgba)
{
const size_t i = y * width + x;
_rgba[i] = rgba;
}
size_t getI(int y) const { return y * width; }
size_t getI(int x, int y) const { return y * width + x; }
void set(size_t i, uint32 rgba) { _rgba[i] = rgba; }

const std::vector<uint32>& getRGBA() const { return _rgba; }
};

void rasterize(FBO &fbo, const Vec3f vtcs[3], const uint32 rgba)
{
// sort vertices by y coordinates
uint iVtcs[3] = { 0, 1, 2 };
if (vtcs[iVtcs[0]].y > vtcs[iVtcs[1]].y) std::swap(iVtcs[0], iVtcs[1]);
if (vtcs[iVtcs[1]].y > vtcs[iVtcs[2]].y) std::swap(iVtcs[1], iVtcs[2]);
if (vtcs[iVtcs[0]].y > vtcs[iVtcs[1]].y) std::swap(iVtcs[0], iVtcs[1]);
const Vec3f vtcsS[3] = { vtcs[iVtcs[0]], vtcs[iVtcs[1]], vtcs[iVtcs[2]] };
const float yM = vtcs[1].y;
// cut triangle in upper and lower part
const float xT = vtcsS[0].x;
float xML = vtcsS[1].x;
const float f = (yM - vtcsS[0].y) / (vtcsS[2].y - vtcsS[0].y);
float xMR = (1.0f - f) * xT + f * vtcsS[2].x;
if (xML > xMR) std::swap(xML, xMR);
// draw upper part of triangle
if (vtcs[iVtcs[0]].y < yM) {
const float dY = yM - vtcsS[0].y;
for (int y = std::max((int)vtcsS[0].y, 0),
yE = std::min((int)(yM + 0.5f), fbo.height);
y < yE; ++y) {
const float f1 = (yM - y) / dY, f0 = 1.0f - f1;
const float xL = f0 * xT + f1 * xML, xR = f0 * xT + f1 * xMR;
const size_t i = fbo.getI(y);
for (int x = std::max((int)xL, 0),
xE = std::min((int)(xR + 0.5f), fbo.width);
x < xE; ++x) {
fbo.set(i + x, rgba);
}
}
} // else upper edge horizontal
// draw lower part of triangle
if (yM < vtcs[2].y) {
const float xB = vtcsS[2].x;
const float dY = vtcsS[2].y - yM;
for (int y = std::max((int)yM, 0),
yE = std::min((int)(vtcsS[2].y + 0.5f), fbo.height);
y < yE; ++y) {
const float f1 = (y - yM) / dY, f0 = 1.0f - f1;
const float xL = f0 * xML + f1 * xB, xR = f0 * xMR + f1 * xB;
const size_t i = fbo.getI(y);
for (int x = std::max((int)xL, 0),
xE = std::min((int)(xR + 0.5f), fbo.width);
x < xE; ++x) {
fbo.set(i + x, rgba);
}
}
} // else lower edge horizontal
}

template <typename VALUE>
Vec3T<VALUE> transformPoint(const Mat4x4T<VALUE> &mat, const Vec3T<VALUE> &pt)
{
Vec4T<VALUE> pt_ = mat * Vec4T<VALUE>(pt.x, pt.y, pt.z, (VALUE)1);
return pt_.w != (VALUE)0
? Vec3T<VALUE>(pt_.x / pt_.w, pt_.y / pt_.w, pt_.z / pt_.w)
: Vec3T<VALUE>(pt_.x, pt_.y, pt_.z);
}

typedef std::chrono::high_resolution_clock HiResClock;
typedef std::chrono::microseconds MicroSecs;

int mainBench()
{
const Mat4x4f matProj(InitScale, 1.0f / Width, 1.0f / Height, 1.0f);
const Mat4x4f matScreen
= Mat4x4f(InitScale, 0.5f * Width, 0.5f * Height, 1.0f)
* Mat4x4f(InitTrans, Vec3f(1.0f, 1.0f, 0.0f));
const Mat4x4f mat = matScreen * matProj /* * matView * matModel */;
FBO fbo(Width, Height);

HiResClock::time_point start = HiResClock::now();
size_t fps = 0;

for (;;) {
static Vec3f v0 = { -2000.0f, -2000.0, 10.0 };
static Vec3f v1 = { 2000.0f, -2000.0, 10.0 };
static Vec3f v2 = { 0.0f, 2000.0, 10.0 };
const Vec3f vtcs[] = {
transformPoint(mat, v0), transformPoint(mat, v1), transformPoint(mat, v2)
};
rasterize(fbo, vtcs, 0xff0000ff);
++fps;

HiResClock::time_point now = HiResClock::now();
auto timeDiff
= std::chrono::duration_cast<MicroSecs>(now - start).count();

static const long oneSecond = 1000000;
if (timeDiff >= oneSecond) {
std::cout << fps << " " << std::flush;
fps = 0;
start = now;
}
}
}

#include <stack>

#include <QtWidgets>

struct RenderContext {
FBO fbo; // frame buffer object
Mat4x4f matModelView;
Mat4x4f matProj;

RenderContext(int width, int height):
fbo(width, height),
matModelView(InitIdent),
matProj(InitIdent)
{ }
~RenderContext() = default;
};

void render(RenderContext &context)
{
context.fbo.clear(0xffffcc88);
static Vec3f v0 = { -2000.0f, -2000.0, 10.0 };
static Vec3f v1 = { 2000.0f, -2000.0, 10.0 };
static Vec3f v2 = { 0.0f, 2000.0, 10.0 };
#if 0 // test transformations of mainBench()
const Mat4x4f matProj(InitScale, 1.0f / Width, 1.0f / Height, 1.0f);
const Mat4x4f matScreen
= Mat4x4f(InitScale, 0.5f * Width, 0.5f * Height, 1.0f)
* Mat4x4f(InitTrans, Vec3f(1.0f, 1.0f, 0.0f));
const Mat4x4f mat = matScreen * matProj /* * matView * matModel */;
#else // make a simple animation
const Mat4x4f matScreen
= Mat4x4f(InitScale, 0.5f * context.fbo.width, 0.5f * context.fbo.height, 1.0f)
* Mat4x4f(InitTrans, Vec3f(1.0f, 1.0f, 0.0f));
const Mat4x4f mat = matScreen * context.matProj * context.matModelView;
#endif // 0
const Vec3f vtcs[] = {
transformPoint(mat, v0), transformPoint(mat, v1), transformPoint(mat, v2)
};
rasterize(context.fbo, vtcs, 0xff0000ff);
}

int main(int argc, char **argv)
{
// evaluate arguments
const bool gui = argc > 1
&& (strcmp(argv[1], "gui") == 0 || strcmp(argv[1], "-gui") == 0);
// without arguments: start benchmark
if (!gui) return mainBench();
// remove argument "gui"for (char **arg = argv + 1; *arg; ++arg) arg [0] = arg[1];
// Qt Demo
qDebug() << "Qt Version:" << QT_VERSION_STR;
QApplication app(argc, argv);
RenderContext context(Width, Height);
// setup GUI
QPixmap qPixmapImg(Width, Height);
QLabel qLblImg;
qLblImg.setWindowTitle("Software Rasterizer Demo");
qLblImg.setPixmap(qPixmapImg);
qLblImg.show();
// Qt timer for periodic rendering/animation
QTime qTime(0, 0);
QTimer qTimer;
qTimer.setInterval(50);
// install signal handlers
QObject::connect(&qTimer, &QTimer::timeout,
[&]() {
// simple animation
const float r = 1.0f, t = 0.001f * qTime.elapsed();
context.matModelView
= Mat4x4f(InitTrans, Vec3f(r * sin(t), r * cos(t), 0.0f))
* Mat4x4f(InitScale, 0.0001f, 0.0001f, 0.0001f);
// rendering
render(context);
// transfer FBO to qLblImg
const QImage qImg((uchar*)context.fbo.getRGBA().data(),
Width, Height, QImage::Format_RGBA8888);
qPixmapImg.convertFromImage(qImg);
qLblImg.setPixmap(qPixmapImg);
});
// runtime loop
qTime.start(); qTimer.start();
return app.exec();
}

Вместо gmtl (что я не знаю), я использовал linmath.h (осталось от ранее MCVEs я писал в прошлом):

#ifndef LIN_MATH_H
#define LIN_MATH_H

#include <iostream>
#include <cassert>
#include <cmath>

double Pi = 3.1415926535897932384626433832795;

template <typename VALUE>
inline VALUE degToRad(VALUE angle)
{
return (VALUE)Pi * angle / (VALUE)180;
}

template <typename VALUE>
inline VALUE radToDeg(VALUE angle)
{
return (VALUE)180 * angle / (VALUE)Pi;
}

template <typename VALUE>
struct Vec2T {
VALUE x, y;
Vec2T() { }
Vec2T(VALUE x, VALUE y): x(x), y(y) { }
};
template <typename VALUE>
VALUE length(const Vec2T<VALUE> &vec)
{
return sqrt(vec.x * vec.x + vec.y * vec.y);
}
template <typename VALUE>
std::ostream& operator<<(std::ostream &out, const Vec2T<VALUE> &v)
{
return out << "( " << v.x << ", " << v.y << " )";
}

typedef Vec2T<float> Vec2f;
typedef Vec2T<double> Vec2;

template <typename VALUE>
struct Vec3T {
VALUE x, y, z;
Vec3T() { }
Vec3T(VALUE x, VALUE y, VALUE z): x(x), y(y), z(z) { }
Vec3T(const Vec2T<VALUE> &xy, VALUE z): x(xy.x), y(xy.y), z(z) { }
explicit operator Vec2T<VALUE>() const { return Vec2T<VALUE>(x, y); }
};
template <typename VALUE>
std::ostream& operator<<(std::ostream &out, const Vec3T<VALUE> &v)
{
return out << "( " << v.x << ", " << v.y << ", " << v.z << " )";
}

typedef Vec3T<float> Vec3f;
typedef Vec3T<double> Vec3;

template <typename VALUE>
struct Vec4T {
VALUE x, y, z, w;
Vec4T() { }
Vec4T(VALUE x, VALUE y, VALUE z, VALUE w): x(x), y(y), z(z), w(w) { }
Vec4T(const Vec2T<VALUE> &xy, VALUE z, VALUE w):
x(xy.x), y(xy.y), z(z), w(w)
{ }
Vec4T(const Vec3T<VALUE> &xyz, VALUE w):
x(xyz.x), y(xyz.y), z(xyz.z), w(w)
{ }
explicit operator Vec2T<VALUE>() const { return Vec2T<VALUE>(x, y); }
explicit operator Vec3T<VALUE>() const { return Vec3T<VALUE>(x, y, z); }
};
template <typename VALUE>
std::ostream& operator<<(std::ostream &out, const Vec4T<VALUE> &v)
{
return out << "( " << v.x << ", " << v.y << ", " << v.z << ", " << v.w << " )";
}

typedef Vec4T<float> Vec4f;
typedef Vec4T<double> Vec4;

enum ArgInitIdent { InitIdent };
enum ArgInitTrans { InitTrans };
enum ArgInitRot { InitRot };
enum ArgInitRotX { InitRotX };
enum ArgInitRotY { InitRotY };
enum ArgInitRotZ { InitRotZ };
enum ArgInitScale { InitScale };

template <typename VALUE>
struct Mat4x4T {
union {
VALUE comp[4 * 4];
struct {
VALUE _00, _01, _02, _03;
VALUE _10, _11, _12, _13;
VALUE _20, _21, _22, _23;
VALUE _30, _31, _32, _33;
};
};

// constructor to build a matrix by elements
Mat4x4T(
VALUE _00, VALUE _01, VALUE _02, VALUE _03,
VALUE _10, VALUE _11, VALUE _12, VALUE _13,
VALUE _20, VALUE _21, VALUE _22, VALUE _23,
VALUE _30, VALUE _31, VALUE _32, VALUE _33):
_00(_00), _01(_01), _02(_02), _03(_03),
_10(_10), _11(_11), _12(_12), _13(_13),
_20(_20), _21(_21), _22(_22), _23(_23),
_30(_30), _31(_31), _32(_32), _33(_33)
{ }
// constructor to build an identity matrix
Mat4x4T(ArgInitIdent):
_00((VALUE)1), _01((VALUE)0), _02((VALUE)0), _03((VALUE)0),
_10((VALUE)0), _11((VALUE)1), _12((VALUE)0), _13((VALUE)0),
_20((VALUE)0), _21((VALUE)0), _22((VALUE)1), _23((VALUE)0),
_30((VALUE)0), _31((VALUE)0), _32((VALUE)0), _33((VALUE)1)
{ }
// constructor to build a matrix for translation
Mat4x4T(ArgInitTrans, const Vec3T<VALUE> &t):
_00((VALUE)1), _01((VALUE)0), _02((VALUE)0), _03((VALUE)t.x),
_10((VALUE)0), _11((VALUE)1), _12((VALUE)0), _13((VALUE)t.y),
_20((VALUE)0), _21((VALUE)0), _22((VALUE)1), _23((VALUE)t.z),
_30((VALUE)0), _31((VALUE)0), _32((VALUE)0), _33((VALUE)1)
{ }
// constructor to build a matrix for rotation about axis
Mat4x4T(ArgInitRot, const Vec3T<VALUE> &axis, VALUE angle):
_03((VALUE)0), _13((VALUE)0), _23((VALUE)0),
_30((VALUE)0), _31((VALUE)0), _32((VALUE)0), _33((VALUE)1)
{
//axis.normalize();
const VALUE sinAngle = sin(angle), cosAngle = cos(angle);
const VALUE xx = axis.x * axis.x, xy = axis.x * axis.y;
const VALUE xz = axis.x * axis.z, yy = axis.y * axis.y;
const VALUE yz = axis.y * axis.z, zz = axis.z * axis.z;
_00 = xx + cosAngle * ((VALUE)1 - xx) /* + sinAngle * 0 */;
_01 = xy - cosAngle * xy - sinAngle * axis.z;
_02 = xz - cosAngle * xz + sinAngle * axis.y;
_10 = xy - cosAngle * xy + sinAngle * axis.z;
_11 = yy + cosAngle * ((VALUE)1 - yy) /* + sinAngle * 0 */;
_12 = yz - cosAngle * yz - sinAngle * axis.x;
_20 = xz - cosAngle * xz - sinAngle * axis.y;
_21 = yz - cosAngle * yz + sinAngle * axis.x;
_22 = zz + cosAngle * ((VALUE)1 - zz) /* + sinAngle * 0 */;
}
// constructor to build a matrix for rotation about x axis
Mat4x4T(ArgInitRotX, VALUE angle):
_00((VALUE)1), _01((VALUE)0),    _02((VALUE)0),   _03((VALUE)0),
_10((VALUE)0), _11(cos(angle)),  _12(-sin(angle)), _13((VALUE)0),
_20((VALUE)0), _21(sin(angle)), _22(cos(angle)), _23((VALUE)0),
_30((VALUE)0), _31((VALUE)0),    _32((VALUE)0),   _33((VALUE)1)
{ }
// constructor to build a matrix for rotation about y axis
Mat4x4T(ArgInitRotY, VALUE angle):
_00(cos(angle)), _01((VALUE)0), _02(sin(angle)), _03((VALUE)0),
_10((VALUE)0),   _11((VALUE)1), _12((VALUE)0),    _13((VALUE)0),
_20(-sin(angle)), _21((VALUE)0), _22(cos(angle)),  _23((VALUE)0),
_30((VALUE)0), _31((VALUE)0),    _32((VALUE)0),   _33((VALUE)1)
{ }
// constructor to build a matrix for rotation about z axis
Mat4x4T(ArgInitRotZ, VALUE angle):
_00(cos(angle)),  _01(-sin(angle)), _02((VALUE)0), _03((VALUE)0),
_10(sin(angle)), _11(cos(angle)), _12((VALUE)0), _13((VALUE)0),
_20((VALUE)0),    _21((VALUE)0),   _22((VALUE)1), _23((VALUE)0),
_30((VALUE)0),    _31((VALUE)0),   _32((VALUE)0), _33((VALUE)1)
{ }
// constructor to build a matrix for scaling
Mat4x4T(ArgInitScale, VALUE sx, VALUE sy, VALUE sz):
_00((VALUE)sx), _01((VALUE)0),  _02((VALUE)0),  _03((VALUE)0),
_10((VALUE)0),  _11((VALUE)sy), _12((VALUE)0),  _13((VALUE)0),
_20((VALUE)0),  _21((VALUE)0),  _22((VALUE)sz), _23((VALUE)0),
_30((VALUE)0),  _31((VALUE)0),  _32((VALUE)0),  _33((VALUE)1)
{ }
// operator to allow access with [][]
double* operator [] (int i)
{
assert(i >= 0 && i < 4);
return comp + 4 * i;
}
// operator to allow access with [][]
const double* operator [] (int i) const
{
assert(i >= 0 && i < 4);
return comp + 4 * i;
}
// multiply matrix with matrix -> matrix
Mat4x4T operator * (const Mat4x4T &mat) const
{
return Mat4x4T(
_00 * mat._00 + _01 * mat._10 + _02 * mat._20 + _03 * mat._30,
_00 * mat._01 + _01 * mat._11 + _02 * mat._21 + _03 * mat._31,
_00 * mat._02 + _01 * mat._12 + _02 * mat._22 + _03 * mat._32,
_00 * mat._03 + _01 * mat._13 + _02 * mat._23 + _03 * mat._33,
_10 * mat._00 + _11 * mat._10 + _12 * mat._20 + _13 * mat._30,
_10 * mat._01 + _11 * mat._11 + _12 * mat._21 + _13 * mat._31,
_10 * mat._02 + _11 * mat._12 + _12 * mat._22 + _13 * mat._32,
_10 * mat._03 + _11 * mat._13 + _12 * mat._23 + _13 * mat._33,
_20 * mat._00 + _21 * mat._10 + _22 * mat._20 + _23 * mat._30,
_20 * mat._01 + _21 * mat._11 + _22 * mat._21 + _23 * mat._31,
_20 * mat._02 + _21 * mat._12 + _22 * mat._22 + _23 * mat._32,
_20 * mat._03 + _21 * mat._13 + _22 * mat._23 + _23 * mat._33,
_30 * mat._00 + _31 * mat._10 + _32 * mat._20 + _33 * mat._30,
_30 * mat._01 + _31 * mat._11 + _32 * mat._21 + _33 * mat._31,
_30 * mat._02 + _31 * mat._12 + _32 * mat._22 + _33 * mat._32,
_30 * mat._03 + _31 * mat._13 + _32 * mat._23 + _33 * mat._33);
}
// multiply matrix with vector -> vector
Vec4T<VALUE> operator * (const Vec4T<VALUE> &vec) const
{
return Vec4T<VALUE>(
_00 * vec.x + _01 * vec.y + _02 * vec.z + _03 * vec.w,
_10 * vec.x + _11 * vec.y + _12 * vec.z + _13 * vec.w,
_20 * vec.x + _21 * vec.y + _22 * vec.z + _23 * vec.w,
_30 * vec.x + _31 * vec.y + _32 * vec.z + _33 * vec.w);
}
};

template <typename VALUE>
std::ostream& operator<<(std::ostream &out, const Mat4x4T<VALUE> &m)
{
return out
<< m._00 << '\t' << m._01 << '\t' << m._02 << '\t' << m._03 << '\n'
<< m._10 << '\t' << m._11 << '\t' << m._12 << '\t' << m._13 << '\n'
<< m._20 << '\t' << m._21 << '\t' << m._22 << '\t' << m._23 << '\n'
<< m._30 << '\t' << m._31 << '\t' << m._32 << '\t' << m._33 << '\n';
}
typedef Mat4x4T<float> Mat4x4f;
typedef Mat4x4T<double> Mat4x4;

// enumeration of rotation axes
enum RotAxis {
RotX, // rotation about x axis
RotY, // rotation about y axis
RotZ // rotation about z axis
};

// enumeration of possible Euler angles
enum EulerAngle {
RotXYX = RotX + 3 * RotY + 9 * RotX, // 0 + 3 + 0 = 3
RotXYZ = RotX + 3 * RotY + 9 * RotZ, // 0 + 3 + 18 = 21
RotXZX = RotX + 3 * RotZ + 9 * RotX, // 0 + 6 + 0 = 6
RotXZY = RotX + 3 * RotZ + 9 * RotY, // 0 + 6 + 9 = 15
RotYXY = RotY + 3 * RotX + 9 * RotY, // 1 + 0 + 9 = 10
RotYXZ = RotY + 3 * RotX + 9 * RotZ, // 1 + 0 + 18 = 19
RotYZX = RotY + 3 * RotZ + 9 * RotX, // 1 + 6 + 0 = 7
RotYZY = RotY + 3 * RotZ + 9 * RotY, // 1 + 6 + 9 = 16
RotZXY = RotZ + 3 * RotX + 9 * RotY, // 2 + 0 + 9 = 11
RotZXZ = RotZ + 3 * RotX + 9 * RotZ, // 2 + 0 + 18 = 20
RotZYX = RotZ + 3 * RotY + 9 * RotX, // 2 + 3 + 0 = 5
RotZYZ = RotZ + 3 * RotY + 9 * RotZ, // 2 + 3 + 18 = 23
RotHPR = RotZXY, // used in OpenGL Performer
RotABC = RotZYX // used in German engineering
};

/* decomposes the combined EULER angle type into the corresponding
* individual EULER angle axis types.
*/
inline void decompose(
EulerAngle type, RotAxis &axis1, RotAxis &axis2, RotAxis &axis3)
{
unsigned type_ = (unsigned)type;
axis1 = (RotAxis)(type_ % 3); type_ /= 3;
axis2 = (RotAxis)(type_ % 3); type_ /= 3;
axis3 = (RotAxis)type_;
}

template <typename VALUE>
Mat4x4T<VALUE> makeEuler(
EulerAngle mode, VALUE rot1, VALUE rot2, VALUE rot3)
{
RotAxis axis1, axis2, axis3;
decompose(mode, axis1, axis2, axis3);
const static VALUE axes[3][3] = {
{ (VALUE)1, (VALUE)0, (VALUE)0 },
{ (VALUE)0, (VALUE)1, (VALUE)0 },
{ (VALUE)0, (VALUE)0, (VALUE)1 }
};
return
Mat4x4T<VALUE>(InitRot,
Vec3T<VALUE>(axes[axis1][0], axes[axis1][1], axes[axis1][2]),
rot1)
* Mat4x4T<VALUE>(InitRot,
Vec3T<VALUE>(axes[axis2][0], axes[axis2][1], axes[axis2][2]),
rot2)
* Mat4x4T<VALUE>(InitRot,
Vec3T<VALUE>(axes[axis3][0], axes[axis3][1], axes[axis3][2]),
rot3);
}

/* decomposes a rotation matrix into EULER angles.
*
* It is necessary that the upper left 3x3 matrix is composed of rotations
* only. Translational parts are not considered.
* Other transformations (e.g. scaling, shearing, projection) may cause
* wrong results.
*/
template <typename VALUE>
void decompose(
const Mat4x4T<VALUE> &mat,
RotAxis axis1, RotAxis axis2, RotAxis axis3,
VALUE &angle1, VALUE &angle2, VALUE &angle3)
{
assert(axis1 != axis2 && axis2 != axis3);
/* This is ported from EulerAngles.h of the Eigen library. */
const int odd = (axis1 + 1) % 3 == axis2 ? 0 : 1;
const int i = axis1;
const int j = (axis1 + 1 + odd) % 3;
const int k = (axis1 + 2 - odd) % 3;
if (axis1 == axis3) {
angle1 = atan2(mat[j][i], mat[k][i]);
if ((odd && angle1 < (VALUE)0) || (!odd && angle1 > (VALUE)0)) {
angle1 = angle1 > (VALUE)0 ? angle1 - (VALUE)Pi : angle1 + (VALUE)Pi;
const VALUE s2 = length(Vec2T<VALUE>(mat[j][i], mat[k][i]));
angle2 = -atan2(s2, mat[i][i]);
} else {
const VALUE s2 = length(Vec2T<VALUE>(mat[j][i], mat[k][i]));
angle2 = atan2(s2, mat[i][i]);
}
const VALUE s1 = sin(angle1);
const VALUE c1 = cos(angle1);
angle3 = atan2(c1 * mat[j][k] - s1 * mat[k][k],
c1 * mat[j][j] - s1 * mat[k][j]);
} else {
angle1 = atan2(mat[j][k], mat[k][k]);
const VALUE c2 = length(Vec2T<VALUE>(mat[i][i], mat[i][j]));
if ((odd && angle1<(VALUE)0) || (!odd && angle1 > (VALUE)0)) {
angle1 = (angle1 > (VALUE)0)
? angle1 - (VALUE)Pi : angle1 + (VALUE)Pi;
angle2 = atan2(-mat[i][k], -c2);
} else angle2 = atan2(-mat[i][k], c2);
const VALUE s1 = sin(angle1);
const VALUE c1 = cos(angle1);
angle3 = atan2(s1 * mat[k][i] - c1 * mat[j][i],
c1 * mat[j][j] - s1 * mat[k][j]);
}
if (!odd) {
angle1 = -angle1; angle2 = -angle2; angle3 = -angle3;
}
}

#endif // LIN_MATH_H

Перед тем, как добавить код Qt, я просто скомпилировал:

$ g++ -std=c++11 -o rasterizerSimple rasterizerSimple.cc

Чтобы скомпилировать с Qt, я написал проект Qt rasterizerSimple.pro:

SOURCES = rasterizerSimple.cc

QT += widgets

Скомпилировано и протестировано на cygwin64 в Windows 10:

$ qmake-qt5 rasterizerSimple.pro

$ make

$ ./rasterizerSimple
2724 2921 3015 2781 2800 2805 2859 2783 2931 2871 2902 2983 2995 2882 2940 2878 3007 2993 3066 3067 3118 3144 2849 3084 3020 3005 3030 2991 2999 3065 2941 3123 3119 2905 3135 2938

CtrlС

В моем ноутбуке установлен Intel i7 (и он немного шумел, когда я позволил запустить программу немного дольше).

Это выглядит не так уж плохо — в среднем 3000 треугольников в секунду. (Он превосходит 130 FPS OP, если его i7 не намного медленнее, чем мой.)

Может быть, FPS может быть подтолкнул немного больше за счет дальнейших улучшений. Например, интерполяция может быть выполнена с использованием Алгоритм Брезенхема хотя это не появляется в большинстве внутреннего цикла. Чтобы оптимизировать большую часть внутреннего цикла, заполнение горизонтальной линии должно выполняться быстрее (хотя я не совсем уверен, как этого добиться).

Чтобы запустить визуализацию Qt, приложение должно быть запущено с gui:

$ ./rasterizerSimple gui

---

Этот образец вдохновил меня на игрушечный проект No-GL 3D Renderer которые можно найти на github.