Реализация функции Tak с использованием хвостовой рекурсии
Можно ли реализовать Так функция:
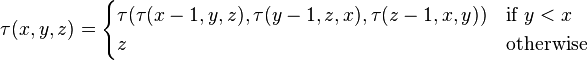
хвост рекурсивно в C / C ++ таким образом, чтобы gcc / g ++ мог выполнять оптимизацию хвостовой рекурсии?
Я не уверен, что вложенные рекурсивные вызовы функций будут путать компилятор.
Решение
Оптимизация хвостовой рекурсии в C ++ требует, чтобы был только 1 рекурсивный вызов (что в основном позволяет преобразовать его в цикл), и что рекурсивный вызов является последней операцией в функции:
Пример:
unsigned int f( unsigned int a )
{
if ( a == 0 )
{
return a;
}
return f( a - 1 ); // tail recursion
}
Поскольку функция Tak требует 4 рекурсивных вызова за «итерацию»:
int tak(int x, int y, int z)
{
if (x >= y)
{
return z;
}
else
{
return tak(tak(x-1, y, z), tak(y-1, z, x), tak(z-1, x, y)); // this is why it cannot happen
}
}
Как видите, последний вызов рекурсивный, но внутри него 3 рекурсивных вызова. Это предотвращает оптимизацию хвостовой рекурсии (и не существует логического метода для преобразования этого в нерекурсивный цикл — что требуется для получения оптимизации хвостовой рекурсии).
Другой способ, которым это может быть реализовано:
int tak(int x, int y, int z)
{
while (x > y)
{
int oldx = x, oldy = y;
x = tak(x - 1, y, z);
y = tak(y - 1, z, oldx);
if (x <= y)
break;
z = tak(z - 1, oldx, oldy);
}
return z;
}
Что еще раз показывает, что даже в форме цикла он все еще рекурсивен, предотвращая оптимизацию хвостовой рекурсии.
Другие решения
Исходя из вашего математического определения, мы можем просто написать функцию как:
int tak(int x, int y, int z){
if(x>y)
return tak(tak(1-x,y,z), tak(y-1,z,x), tak(z-1,x,y));
else
return z;
}
Однако вы не можете сделать это с помощью хвостового набора, поскольку он не может быть преобразован в цикл. Поскольку существует более одного вызова рекрусии.
