разбиение графа на циклы, а затем на пути
Прежде всего, я должен сказать, что я не знаком с теорией графов, и мои знания по математике очень плохие. Во всяком случае, я использую концепции графа для своего анализа.
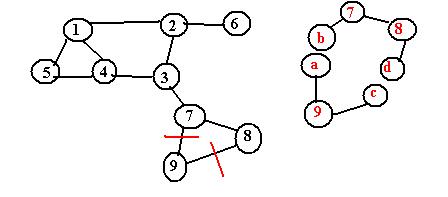
По сути, я разлагаю неориентированный граф (скажем, G) на циклы (замкнутый граф). Особенностью моего цикла является то, что они являются самыми короткими циклами, которые можно пройти между двумя вершинами (поскольку они являются циклом, хотя начало и конец одинаковы). Согласно моему примеру графика, мои циклы (1,4,5,1) (1,2,3,4,1) (7,9,8,7) (я пренебрегаю циклами, длина которых меньше 3) ,
Редактировать: я использую глубину поиска сначала, чтобы получить циклы, а затем получил наименьшие циклы.
Позже я продолжаю торможение этих циклов по направленным путям. Здесь я разорвал циклы по краям (через красные линии на рисунке), так что я вставил начальные и конечные узлы для моих новых графов путей. Таким образом, для цикла (7,9,8,7) => новые направленные пути (а, 9, в) (д, 8,7, б)
Редактировать: дальнейшее разбиение выполняется только для выбранных циклов. Это просто вставка нового вектора и обновление элементов. Любые алгоритмы, связанные с теорией графов, здесь не используются.
Затем я делаю анализ с моими данными.
Я сделал все вышеперечисленное. Итак, моя проблема в том, как описать весь
вещи с математическими обозначениями (без примера, как я сказал). Это очень сложно для меня, так как у меня нет даже основ.
Я пытался и гуглил, но все еще не могу найти способ описать то, что я сделал. Я думаю, то, что я сделал, для тебя ясно.
Итак, не могли бы вы помочь мне, как описать
- разложение неориентированного графа на циклы (кратчайшие циклы)
- Циклический разрыв через ребра и построение графиков с направленными путями (как показано на рисунке)
с математическим обозначением (согласно теории графов)
Я видел, как многие авторы используют разные обозначения и символы для определения графиков и их подграфов, но для себя я не могу определить такие вещи, как мои базовые слишком бедны. Поэтому, пожалуйста, помогите мне сказать это формально, математически. Заранее спасибо.
Я вставил образцы рисунков, чтобы получить представление также.
Примечание: я добавил тэг c ++, так как многие компьютерщики используют теории графов и хотели бы получить ответ.
Решение
Первая проблема, с которой вы можете столкнуться при попытке поместить ваши операции в математическое описание, — это ваше определение «кратчайших циклов», поскольку циклы обычно определяются как последовательность вершин, соединенных ребрами, в которой первый также является последним.
Math crashcourse
По математике график типично описывается двумя наборами V (как вершины) и E (как ребра)
Множество E, состоящее из множеств с двумя элементами, каждый из которых является вершиной.
Такие как
-
В знак равно {v1, v2, …., vn}
-
Е знак равно {…, {vi, vk}, …}
Каждый набор в E соответствует одному ребру в вашем графике.
Как таковой (подключен) дорожка типично определяется как:
Последовательность вершин v1, …., уп со свойством, которое для каждых двух последовательных вершин в последовательности VI а также VI + 1 набор {vi, vi + 1} является элементом множества Е.
(практически говоря: есть край от вершины VI к вершине VI + я)
цикл обычно определяется как путь со свойством: v1 знак равно уп (таким образом, первая вершина также является последней)
С этим определением в вашем примере уже есть последовательность: 1, 4, 1 образует цикл (в математическом смысле)
Таким образом, каждое ребро в вашем графике будет считаться «самым коротким» циклом, в то время как приведенные примеры определенно длиннее!
Вы сказали, что вы
… пренебречь циклами, длина которых меньше 3
это не выглядит плохо как отправная точка для вашего описания. К сожалению, я не совсем понял следующие шаги, которые вы хотите выполнить.
Совет
Мой совет или, по крайней мере, способ решения проблемы, заключается в том, чтобы преобразовать довольно длинное описание в какое-то более короткое алгоритмическое описание, уточнив, как именно вы пытаетесь выполнить задачу. Таким образом, добраться до вашего окончательного описания не должно быть слишком сложно для достижения. Особенно не забудьте сказать, что именно является входом в ваш алгоритм. Даже это не кажется слишком ясным из вашего описания.
- Вы начинаете с уже известного набора «самых коротких» циклов?
- или вам только что дали график в качестве входных данных, и вы должны сами определить «самые короткие» циклы?
- если вы обнаружите их сами, как именно это делается?
Особенно не забудьте рассказать об этой части истории, если она применима, так как она кажется одной из самых важных для вашей проблемы.
Другие решения
Других решений пока нет …
