Расстояние между двумя шестиугольниками на шестиугольной сетке

Правильная явная формула для расстояния с вашей системой координат определяется как:

d((x1,y1),(x2,y2)) = max( abs(x1 - x2),
abs((y1 + floor(x1/2)) - (y2 + floor(x2/2)))
)

Во-первых, вам нужно преобразовать ваши координаты в «математическую» систему координат. Каждые два столбца вы сдвигаете свои координаты на 1 единицу в направлении y. «Математические» координаты (s, t) могут быть вычислены из ваших координат (u, v) следующим образом:

s = u + этаж (v / 2)
t = v

Если вы называете одну из сторон шестиугольников a, базовыми векторами вашей системы координат являются (0, -sqrt (3) a) и (3a / 2, sqrt (3) a / 2). Чтобы найти минимальное расстояние между вашими точками, вам нужно рассчитать манхэттенское расстояние в вашей системе координат, которое задается как | s1-s2 | + | t1-t2 | где s и t координаты в вашей системе. Манхэттенское расстояние охватывает только хождение в направлении ваших базовых векторов, поэтому оно охватывает только хождение так: | /, но не хождение так: | \. Вам нужно преобразовать ваши векторы в другую систему координат с базисными векторами (0, -sqrt (3) a) и (3a / 2, -sqrt (3) a / 2). Координаты в этой системе задаются как s ‘= s-t и t’ = t, поэтому расстояние до Манхэттена в этой системе координат определяется как | s1′-s2 ​​’| + | t1′-t2′ |. Расстояние, которое вы ищете, является минимумом двух вычисленных манхэттенских расстояний. Ваш код будет выглядеть так:

struct point
{
int u;
int v;
}

int dist(point const & p, point const & q)
{
int const ps = p.u + (p.v / 2); // integer division!
int const pt = p.v;
int const qs = q.u + (q.v / 2);
int const qt = q.v;
int const dist1 = abs(ps - qs) + abs(pt - qt);
int const dist2 = abs((ps - pt) - (qs - qt)) + abs(pt - qt);
return std::min(dist1, dist2);
}

Вот что сделал:

Принимая одну клетку в качестве центра (это легко увидеть, если вы выберете 0,0), клетки на расстоянии dY образуют большой шестиугольник (с «радиусом» dY). Одна из вершин этого шестиугольника (dY2,dY). Если dX<=dY2 путь зигзагом к барану большого шестиугольника с расстоянием dY, Если нет, то путь является «диагональю» к вершинам плюс вертикальный путь от вершин ко второй ячейке с добавлением dX-dY2 клетки.

Может лучше понять: led:

dX = abs(x1 - x2);
dY = abs(y1 - y2);
dY2= floor((abs(y1 - y2) +  (y1+1)%2  ) / 2);

Затем:

 d = d((x1,y1),(x2,y2))
= dX < dY2 ? dY : dY + dX-dY2 + y1%2 * dY%2

Публикация здесь после того, как я увидела мой пост в блоге, получила реферальный трафик от другого ответа здесь. Это было отклонено, правильно, потому что это было неправильно; но это была неверная характеристика решения, изложенного в моем посте.

Ваша «волнистая» ось — с точки зрения смещения вашей координаты x в каждом другом ряду — вызовет у вас всевозможные головные боли при попытке определить расстояния или выполнить поиск пути позже, если это для какой-то игры. Шестиугольные сетки естественным образом поддаются трем осям, а «квадратная» сетка шестиугольников оптимально будет иметь некоторые отрицательные координаты, что позволяет упростить математику на расстоянии.

Вот сетка с отображенной (x, y), где x увеличивается внизу справа, а y увеличивается вверх.

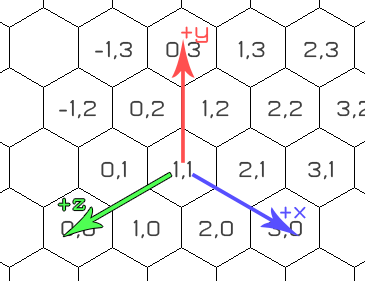
Выпрямляя вещи, третья ось становится очевидной.

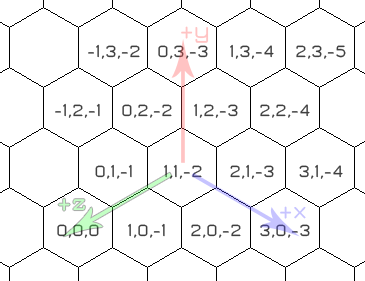
Важно то, что эти три координаты становятся взаимосвязанными — сумма всех трех координат всегда будет равна 0.

При такой согласованной системе координат атомное расстояние между любыми двумя гексами является наибольшим изменением между тремя координатами, или:

d = max( abs(x1 - x2), abs(y1 -y2), abs( (-x1 + -y1) - (-x2 + -y2) )

Довольно просто. Но вы должны сначала исправить свою сетку!

(odd-r) (без z, только x, y)

Я видел некоторые проблемы с реализациями выше. Извините, я не проверял все это, но. Но, возможно, мое решение будет полезно для кого-то, и, возможно, это плохое и не оптимизированное решение.

Основная идея — по диагонали, а затем по горизонтали. Но для этого нужно отметить:

1) Например, у нас есть 0; 3 (x1 = 0; y1 = 3) и чтобы перейти к y2 = 6, мы можем обработать в течение 6 шагов к каждой точке (0-6; 6)
итак: 0-left_border, 6-right_border

2) Рассчитать некоторые смещения

#include <iostream>
#include <cmath>

int main()
{
//while(true){
int x1,y1,x2,y2;
std::cin>>x1>>y1;
std::cin>>x2>>y2;
int diff_y=y2-y1; //only up-> bottom no need abs
int left_x,right_x;
int path;

if( y1>y2 ) { // if Down->Up  then swap
int temp_y=y1;
y1=y2;
y2=temp_y;
//
int temp_x=x1;
x1=x2;
x2=temp_x;
}                   // so now we have Up->Down

// Note that it's odd-r horizontal layout
//OF - Offset Line  (y%2==1)
//NOF -Not Offset Line (y%2==0)
if( y1%2==1 && y2%2==0 ){ //OF ->NOF
left_x = x1 - ( (y2 - y1 + 1)/2 -1 );  //UP->DOWN no need abs
right_x = x1 + (y2 - y1 + 1)/2;  //UP->DOWN no need abs
}
else if( y1%2==0 && y2%2==1 ){ // OF->NOF
left_x = x1 - (y2 - y1 + 1)/2;  //UP->DOWN no need abs
right_x = x1 + ( (y2 - y1 + 1)/2 -1 );  //UP->DOWN no need abs

}
else{
left_x = x1 - (y2 - y1 + 1)/2;  //UP->DOWN no need abs
right_x = x1 + (y2 - y1 + 1)/2;  //UP->DOWN no need abs
}
/////////////////////////////////////////////////////////////
if( x2>=left_x && x2<=right_x ){
path = y2 - y1;
}
else {
int min_1 = std::abs( left_x - x2 );
int min_2 = std::abs( right_x - x2 );
path = y2 - y1 + std::min(min_1, min_2);
}
std::cout<<"Path: "<<path<<"\n\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\n";
//}

return 0;
}

Я верю, что вы ищете ответ:

d((x1,y1),(x2,y2))=max(abs(x1-x2),abs(y1-y2));

Вы можете найти хорошее объяснение гексагональной сетки координат системы / расстояния здесь:

http://keekerdc.com/2011/03/hexagon-grids-coordinate-systems-and-distance-calculations/