Расшифровка одной загадочной строки кода: тригонометрия и определение плоскости
-3 голоса за вопрос, который был правильно написан по теме (с тех пор, как программирование и геометрия не относятся к StackOverflow?) И могли бы помочь однажды представить интересную часть программного обеспечения для рекламы, благодаря помощи людей.
Это было не совсем ясно, но могло бы быть улучшено, если бы люди не понизили это сразу, что является сдерживающим фактором для любого будущего этого вопроса.
Люди имеют здесь неприятную тенденцию отдавать предпочтение понижению голоса, а не протягивать руку помощи. Так много для терпимости и непредубежденности.
Я просто оставлю это изображение в качестве доказательства, что программа, которую я пытался скрыть, является достойным программным обеспечением, которое могло заинтересовать многих. Если он когда-нибудь станет достоянием общественности, то, конечно же, этого не произойдет, благодаря кучке глупых даунвотеров.
Я пытаюсь расшифровать малопонятную часть программы, которую я хочу перенести в форму, удобную для чтения.
Единственная документация, сопровождающая этот фрагмент кода, говорит мне, что мы генерируем случайную плоскость в пространстве из двух «косинусов направления» и расстояния от начала координат.
Я целый день пытался расшифровать программу, и я добился прогресса, но застрял в одной конкретной строке, которая все еще ускользает от меня.
Конкретная линия, кажется, примерно такая: генерирование компонентов a, b, c нормального вектора (которые также являются a, b, c в уравнении плоскости) из двух углов, один из которых, как я понимаю, является углом между ось Z и нормаль, и другой угол между осью X и нормалью.
У всех переменных были непонятные имена, я переименовал несколько, когда понял их значение, в более явные имена. Человек, который написал этот код, больше не здесь, чтобы давать какие-либо объяснения.
Единственный выход, который впоследствии используется, — это три нормальных компонента: normal_a, normal_b и normal_c.
В этой первой части код генерирует случайные параметры для плоскости.
void Plane::generate(int i) // the index of this plane
// as a sequence of planes is being generated here
{
t_pt = (i + 10)*rnd_float() / 2; // this looks a lot like the distance
// from the origin
t_ap = rnd_float() * PI * 2; // rnd_float() returns a rand float between 0 and 1
t_at = rnd_float() * PI * 2;
t_it = (.5 - rnd_float())*PI*.025*COEFF_TRANS; // COEFF_TRANS = 1.5
t_aa = rnd_float() * PI * 2;
t_ia = (.5 - rnd_float())*PI*.0025*.5*COEFF_TRANS;
Затем он определяет координаты нормали вектора
t_at = t_at + t_it; // this is most probably the angle from Z axis to normal
float ptt = t_pt + cos(t_at)*.01*t_pt * t_pt; // <<<<<< the obscure line
normal_c = 1 / (sqrt(1 + ptt*ptt)); // length of normal Z component = c
normal_ab = sqrt(1 - normal_c*normal_c); // length of normal XY component = ab
t_aa = t_aa + t_ia * .31; // this is the other angle, from X or Y axis to normal
float pa = t_ap + cos(t_aa)*.05; // a bit obscure here also
normal_a = normal_ab*cos(pa);
normal_b = normal_ab*sin(pa);
}
Конкретная строка, которая ускользает от меня, это первая строка здесь:
float ptt = t_pt + cos(t_at)*.01*t_pt * t_pt;
normal_c = 1 / (sqrt(1 + ptt*ptt)); // length of normal Z component = c
Мне действительно трудно понять, что может представлять эта переменная ptt.
Если бы мне нужно было вычислить normal_c самостоятельно, я думаю, что это будет включать только косинус и угол.
Если мы переведем код в то, что, как я понимаю, он делает, это будет выглядеть так, но это не поможет мне догадаться, что ptt представляет собой :
float ptt = planeDistance + cos(angleZToNormal)*.01*planeDistance*planeDistance;
Я предположил, что следующая строка, вычисляющая длину z для normal_c, как это делается здесь, вероятно, опирается на формулу: cos (angle) = A / (sqrt (A² + O²)), где A — это длина смежных, а O быть длина противоположной стороны. Но это только предположение.
Будем весьма благодарны за любые указания или подсказки от людей, более опытных в тригонометрии, которые могли бы поставить меня на правильный путь. Спасибо !
Решение
Я все еще не мог сказать вам, что это делает, но я хотел бы поделиться своими успехами, по крайней мере:
float rnd_float() {return rand() / (RAND_MAX + 1.0f);}
void generate(int i) // the index of this plane
// as a sequence of planes is being generated here
{
// generate a random angle B and offset it a bit, randomly
float angle_B = rnd_float() * 2.0f * PI, // angle from 0 to 2 pi
offset_B = (0.5f - rnd_float()) * PI // angle from -pi to pi,
* (.025f * COEFF_TRANS); // times some scaling factor
angle_B += offset_B; // offset the angle B// generate a random angle C and offset it a bit, randomly
float angle_C = rnd_float() * 2.0f * PI, // angle from 0 to 2 pi
offset_C = (0.5f - rnd_float()) * PI // angle from -pi to pi,
* (.0025f * .5f * COEFF_TRANS) * .31f; // times two scaling factors
angle_C += offset_C; // offset the angle D// some sort of distance?
float dist = (i + 10) * rnd_float() / 2;
// generate a random angle A from 0 to 2 pi
float angle_A = rnd_float() * 2.0f * PI;
// no idea
float ptt = dist + cos(angle_B) * dist * dist * 0.01f;
// ditto
float pa = angle_A + cos(angle_C) * .05f;// still not sure what they're doing here, but rearraged it a bit
float normal_c = 1 / sqrt(1 + ptt * ptt), // length of normal Z?
normal_ab = abs(ptt) / sqrt(1 + ptt * ptt); // length of normal XY?
float normal_a = normal_ab * cos(pa);
normal_b = normal_ab * sin(pa);
}
Обратите внимание, что
t_pt -> dist
t_ap -> angle_A
t_at -> angle_B
t_aa -> angle_C
Следует отметить, что сгенерированные значения a, b и c составляют правильно нормализованный единичный вектор и многократно выполняют ваш код для разных i дает следующее:
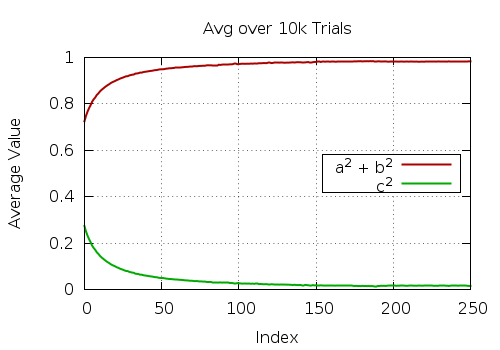
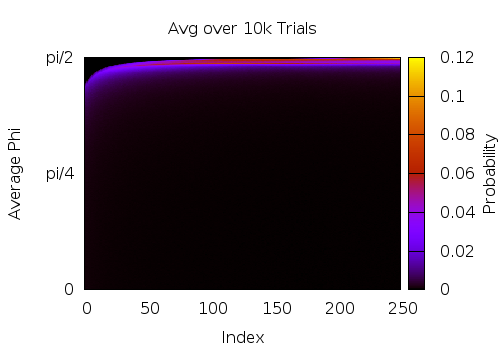
Другие решения
