Главная » C++ » Расчет уравнения теплопроводности становится неустойчивым для различных матриц дифференцирования

Расчет уравнения теплопроводности становится неустойчивым для различных матриц дифференцирования

Я хотел бы решить уравнение теплопроводности в одном измерении, используя алгоритм RK4. Теперь я могу написать уравнение теплопроводности как 

d_t u = d_x(A d_x u)

или же

d_t u = A d_x^2(u)

с A постоянная.
Я хотел сравнить оба метода, и поэтому написал следующий код:

#include <iostream>
#include <math.h>
#include <armadillo>

#define Y0 0
#define Y1 1
#define YSIZE 400
#define ALPHA 1

auto rk4(double f(double, double))
{
return
[       f            ](double t, double y, double dt ) -> double{ return
[t,y,dt,f            ](                    double dy1) -> double{ return
[t,y,dt,f,dy1        ](                    double dy2) -> double{ return
[t,y,dt,f,dy1,dy2    ](                    double dy3) -> double{ return
[t,y,dt,f,dy1,dy2,dy3](                    double dy4) -> double{ return
( dy1 + 2*dy2 + 2*dy3 + dy4 ) / 6   ;} (
dt * f( t+dt  , y+dy3   )          );} (
dt * f( t+dt/2, y+dy2/2 )          );} (
dt * f( t+dt/2, y+dy1/2 )          );} (
dt * f( t     , y       )          );} ;
}

auto rk4(arma::colvec f(double, arma::colvec))
{
return
[       f            ](double t, arma::colvec y, double dt ) -> arma::colvec{ return
[t,y,dt,f            ](                    arma::colvec dy1) -> arma::colvec{ return
[t,y,dt,f,dy1        ](                    arma::colvec dy2) -> arma::colvec{ return
[t,y,dt,f,dy1,dy2    ](                    arma::colvec dy3) -> arma::colvec{ return
[t,y,dt,f,dy1,dy2,dy3](                    arma::colvec dy4) -> arma::colvec{ return
( dy1 + 2*dy2 + 2*dy3 + dy4 ) / 6   ;} (
dt * f( t+dt  , y+dy3   )          );} (
dt * f( t+dt/2, y+dy2/2 )          );} (
dt * f( t+dt/2, y+dy1/2 )          );} (
dt * f( t     , y       )          );} ;
}

void create_first_derivative_matrix(const size_t size, arma::mat &matrix, double dh = -1)
{
if(dh <= 0)
dh = ((double)Y1 - (double)Y0) / ((double)YSIZE - 1.);
matrix = arma::mat(size, size, arma::fill::zeros);
matrix.diag(1) = arma::colvec(size - 1, arma::fill::ones) * 8;
matrix.diag(-1) = arma::colvec(size - 1, arma::fill::ones) * -8;
matrix.diag(2) = arma::colvec(size - 2, arma::fill::ones) * -1;
matrix.diag(-2) = arma::colvec(size - 2, arma::fill::ones);

#ifdef USE_REFLECT
matrix(0, 0) = 0;
matrix(0, 1) = 0;
matrix(0, 2) = 0;
matrix(0, 3) = 0;
matrix(0, 4) = 0;
matrix(1, 0) = -8;
matrix(1, 1) = 1;
matrix(1, 2) = 8;
matrix(1, 3) = -1;
matrix(1, 4) = 0;
matrix(size - 1, size - 1) = 0;
matrix(size - 1, size - 2) = 0;
matrix(size - 1, size - 3) = 0;
matrix(size - 1, size - 4) = 0;
matrix(size - 1, size - 5) = 0;
matrix(size - 2, size - 1) = 8;
matrix(size - 2, size - 2) = -1;
matrix(size - 2, size - 3) = -8;
matrix(size - 2, size - 4) = 1;
matrix(size - 2, size - 5) = 0;
#else
matrix(0, 0) = -25;
matrix(0, 1) = 48;
matrix(0, 2) = -36;
matrix(0, 3) = 16;
matrix(0, 4) = -3;
matrix(1, 0) = -3;
matrix(1, 1) = -10;
matrix(1, 2) = 18;
matrix(1, 3) = -6;
matrix(1, 4) = 1;
matrix(size - 1, size - 1) = 25;
matrix(size - 1, size - 2) = -48;
matrix(size - 1, size - 3) = 36;
matrix(size - 1, size - 4) = -16;
matrix(size - 1, size - 5) = 3;
matrix(size - 2, size - 1) = 3;
matrix(size - 2, size - 2) = 10;
matrix(size - 2, size - 3) = -18;
matrix(size - 2, size - 4) = 6;
matrix(size - 2, size - 5) = -1;
#endif
matrix = matrix / (12 * dh);
}

void create_second_derivative_matrix(const size_t size, arma::mat &matrix, double dh = -1)
{
if(dh <= 0)
dh = ((double)Y1 - (double)Y0) / ((double)YSIZE - 1.);
matrix = arma::mat(size, size, arma::fill::zeros);
matrix.diag(1) = arma::colvec(size - 1, arma::fill::ones) * 16;
matrix.diag(-1) = arma::colvec(size - 1, arma::fill::ones) * 16;
matrix.diag(2) = arma::colvec(size - 2, arma::fill::ones) * -1;
matrix.diag(-2) = arma::colvec(size - 2, arma::fill::ones) * -1;
matrix.diag(0) = arma::colvec(size, arma::fill::ones) * -30;
matrix(0, 0) = 35;
matrix(0, 1) = -104;
matrix(0, 2) = 114;
matrix(0, 3) = -56;
matrix(0, 4) = 11;
matrix(1, 0) = 11;
matrix(1, 1) = -20;
matrix(1, 2) = 6;
matrix(1, 3) = 4;
matrix(1, 4) = -1;
matrix(size - 1, size - 1) = 35;
matrix(size - 1, size - 2) = -104;
matrix(size - 1, size - 3) = 114;
matrix(size - 1, size - 4) = -56;
matrix(size - 1, size - 5) = 11;
matrix(size - 2, size - 1) = 11;
matrix(size - 2, size - 2) = -20;
matrix(size - 2, size - 3) = 6;
matrix(size - 2, size - 4) = 4;
matrix(size - 2, size - 5) = -1;
matrix = matrix / (12 * dh * dh);
}

arma::colvec eval_heat_eqn(const double t, const arma::colvec y)
{
(void) t;
arma::mat deriv_matrix;
#define USE_FIRST_ORDER
#ifdef USE_FIRST_ORDER
create_first_derivative_matrix(y.size(), deriv_matrix);
#else
create_second_derivative_matrix(y.size(), deriv_matrix);
#endif
arma::colvec heat_vec = arma::colvec(y.size(), arma::fill::zeros);
arma::colvec alpha_vec = arma::colvec(y.size(), arma::fill::ones) * ALPHA;

arma::mat alpha_mat = arma::mat(y.size(), y.size(), arma::fill::zeros);
alpha_mat.diag() = alpha_vec;
for(size_t i = 0; i < y.size(); ++i)
if(i >= 0.5 * y.size())
heat_vec(i) = 0.01;
else
heat_vec(i) = 0;
#ifdef USE_FIRST_ORDER
return alpha_mat * ((deriv_matrix * deriv_matrix) * y) + heat_vec;
#else
return alpha_mat * (deriv_matrix * y) + heat_vec;
#endif
}

//Prints a vector
void print_vector(const arma::colvec &x, const arma::colvec &vector_data, std::string filename)
{
std::ofstream out(filename.c_str());
for(size_t i = 0; i < vector_data.size(); ++i)
out << x(i) << '\t' << abs(vector_data[i]) << '\n';
out.close();
}

int main(void)
{
const double TIME_MAXIMUM = 10, WHOLE_TOLERANCE = 1e-12 ;
const double T_START = 0.0;
double DT = 0.00010;
arma::mat local_deriv_matrix_I, local_deriv_matrix_II;

auto is_whole      = [WHOLE_TOLERANCE](double t          )->bool  { return fabs(t-round(t)) < WHOLE_TOLERANCE; } ;

double t = T_START ;
const double stability_value = ALPHA /(pow(((double)Y1 - (double)Y0) / ((double)YSIZE + 1.), 2));
DT = 0.15 / stability_value;
std::cout << "Stability: " << ALPHA * DT/(pow(((double)Y1 - (double)Y0) / ((double)YSIZE + 1.), 2)) << '\n';
std::cout << "DT: " << DT << '\n';auto dy_vec = rk4( eval_heat_eqn ) ;

arma::colvec y_vec = arma::colvec(YSIZE, arma::fill::ones);//
arma::colvec test_vec = arma::linspace(Y0, Y1, YSIZE);
arma::colvec x_vec = arma::linspace(Y0, Y1, y_vec.size());
test_vec = arma::pow(test_vec, 3);
create_first_derivative_matrix(y_vec.size(), local_deriv_matrix_I);
create_second_derivative_matrix(y_vec.size(), local_deriv_matrix_II);

arma::colvec deriv_vec = local_deriv_matrix_I * test_vec;
print_vector(x_vec, test_vec, "test_vector.txt");
print_vector(x_vec, deriv_vec, "derivation_vector.txt");
deriv_vec = local_deriv_matrix_I * local_deriv_matrix_I * test_vec;
print_vector(x_vec, deriv_vec, "derivation_II_vector.txt");
deriv_vec = local_deriv_matrix_II * test_vec;
print_vector(x_vec, deriv_vec, "II_derivation_vector.txt");

t = T_START ;
std::vector<arma::colvec> results;

while(t <= TIME_MAXIMUM) {
if (is_whole(t)) { printf("y(%4.2f)[0]\t=(%12.6f)\n", t, y_vec[0]); }
y_vec += dy_vec(t,y_vec,DT) ; t += DT; results.push_back(y_vec);
}

arma::mat result_matrix = arma::mat(y_vec.size(), results.size(), arma::fill::zeros);
for(size_t i = 0; i < results.size(); ++i)
if(i % 100 == 0)
result_matrix.col(i) = results[i];
result_matrix.save("heat_results.txt", arma::raw_ascii);
return 0;
}

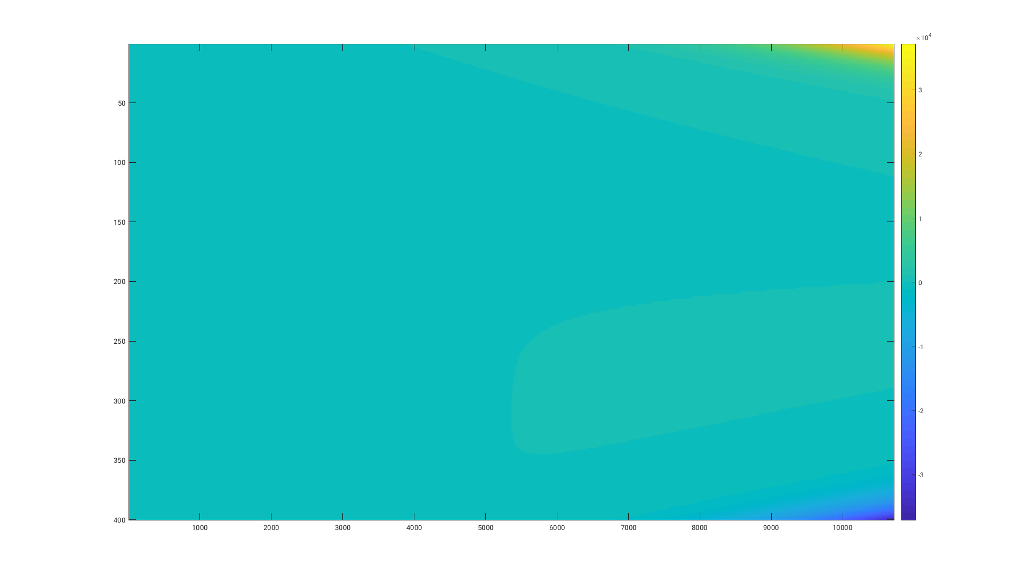
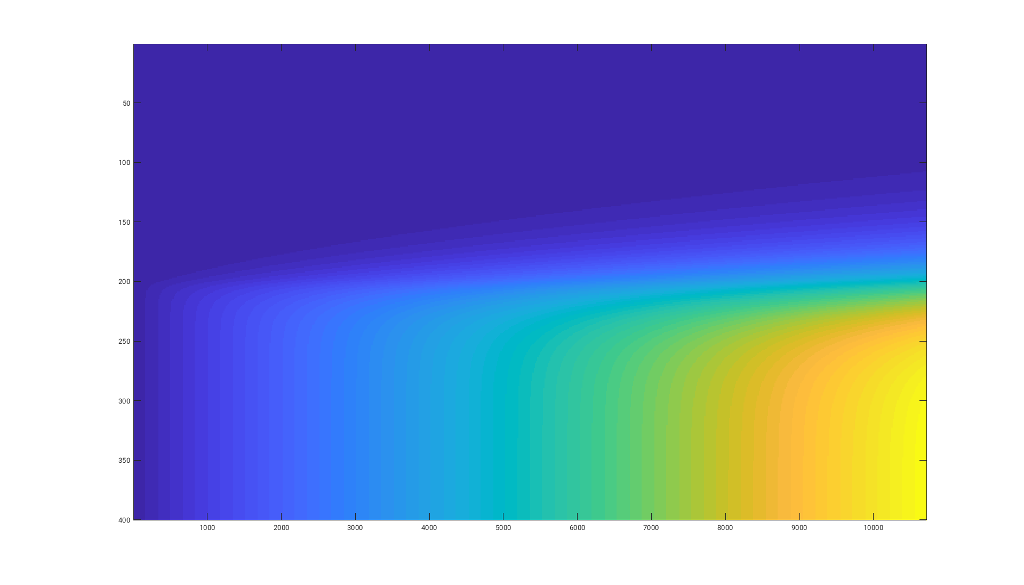
Теперь при запуске этой программы для #define USE_FIRST_ORDER (т.е. используя первый подход) мой результат выглядит введите описание изображения здесь
в то время как при непосредственном использовании матрицы второго порядка я получаю другой результат (который является правильным по сравнению с версией первого порядка):
введите описание изображения здесь
Для отладки я сравнил матрицу M1 (первый заказ) и M2 (второй порядок) при умножении на вектор:

M1*M1*y=M2*y

получить одинаковый результат с обеих сторон. Таким образом, я предполагаю, что у меня есть проблема где-то еще, но я не могу ее найти.

2

Решение

Задача ещё не решена.

Другие решения

Других решений пока нет …

Источник
По вопросам рекламы [email protected]
Web-Answers © 2024 Наверх