random — эксперимент с монетой в C ++ с использованием std :: rand (), дающий неверный результат
Я пытаюсь посчитать количество вхождений строки HHHHHHTTTTTT в 1 миллион сальто. Для броска монеты я использую простой метод std :: rand ()% 2. Код ниже. Математически ожидаемый ответ
(10 ^ 6 — 12 + 1) / 2 ^ 12 = 244
Я получил этот результат из вероятностного учебника. Но мой код постоянно получает только около половины этого, то есть около 122. Это проблема с использованием std :: rand () в качестве алгоритма подбрасывания монеты, или в моем коде есть ошибка?
#include <iostream>
#include <cstdlib>
#include <vector>
#include <ctime>
using std::vector;
bool coin_flip(){
return std::rand() % 2;
}
int count_string(int n, const vector<bool>& s){
int k=0, res=0;
for(int i=0; i<n; i++){
if(coin_flip()==s[k]){
k++;
if(k==s.size()){
res++;
k=0;
}
}else{
k=0;
}
}
return res;
}
int main(){
std::srand(std::time(0));
vector<bool> v(12);
const int a[12] = {1,1,1,1,1,1,0,0,0,0,0,0};
for(int i=0; i<12; i++){
v[i] = a[i];
}
std::cout << count_string(1000000, v) << '\n';
return 0;
}
Решение
Давайте представим, что мы просто ищем цепочку для монет HT, Мы начинаем, ожидая головы. Если первый бросок монеты — это головы, отлично, мы переходим к ожиданию хвостов. Теперь, что произойдет, если второй бросок монеты выпадет в голову? Это не соответствует нашим ожиданиям, поэтому мы должны начать все сначала но тогда мы могли бы считать это первым поворотом нашей новой последовательности! То есть наш следующий штат должен ожидать хвостов.
Но это не то, что сейчас делает ваш код. Вы возвращаетесь к началу и возвращаетесь к ожидающим головам для третьей монеты. Вторая монета в основном исчезает в эфире для вас. В результате вы не можете найти HT в HHT,
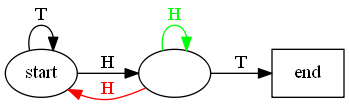
Наглядно, ваш поиск использует красный переход состояния вместо зеленого:
Экстраполируя, вы в настоящее время хотите 6 голов подряд, а затем 6 хвостов. Но седьмая голова возвращается к началу, и вы снова начинаете ожидать 6 голов, вместо того, чтобы учесть 7+ голов. Поскольку 7-й бросок выходит наполовину, вы теряете половину положительных событий.
Другие решения
Других решений пока нет …