Проверка того, является ли многоугольник слабо простым
Я не могу придумать алгоритм для обнаружения слабо простых многоугольников (то есть многоугольников, где стороны могут касаться, но не пересекаются). В настоящее время я просто проверяю пересечения между каждой стороной — вот функция, которую я вызываю для всех несмежных сторон. Таким образом, разрешены только простые полигоны (вообще не трогать). Полигоны являются векторами точек.
bool linesIntersect(const point &a1, const point &a2, const point &b1, const point &b2) {
// Solve intersection of parametric lines using inverse matrix
// The equation of the parametric lines are line1 = (a2 - a1)*s + a1
// and line2 = (b2 - b1)*t + b1, where a1, a2, etc. are vectors.
// Two equations can be produced from the two components, and these
// this system of two equations can be solved for s and t
// If the parameters s and t are between 0 and 1, it means that the lines intersect
float x21 = a2.x - a1.x, x43 = b2.x - b1.x, x31 = b1.x - a1.x,
y21 = a2.y - a1.y, y43 = b2.y - b1.y, y31 = b1.y - a1.y;
float determinant = x43*y21 - x21*y43;
if(determinant == 0.) return false;
float s = float(x43*y31 - x31*y43)/determinant;
float t = float(x21*y31 - x31*y21)/determinant;
if(s <= 1. && s >= 0. && t <= 1. && t >= 0.) return true; // lines intersect
return false;
}
С помощью s < 1. && s > 0. && t < 1. && t > 0. не работает, потому что он принимает некоторые сложные многоугольники как простые.
Первая цифра в этот вопрос показывает пару примеров. Ниже приведен типичный слабо простой многоугольник, с которым будет иметь дело программа.
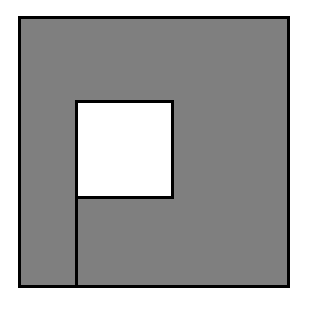
Я предпочел бы псевдокод, так как математический жаргон в вышеупомянутом вопросе (1) меня пугает, и я не думаю, что у меня есть знания для реализации какого-либо сложного алгоритма. Я использую Boost.Polygon для чего-то другого, если там что-то есть, но я ничего не нашел.
РЕДАКТИРОВАТЬ:
Вот как я использую функцию. checkPts является vector<point> с предполагаемой стороной от последней точки к первой.
// Check for self-intersecting polygons
for(int i = 0; i < checkPts.size() - 2; ++i) {
for(int j = i + 2; j < checkPts.size() - 2; ++j) {
if(linesIntersect(checkPts[i], checkPts[i+1], checkPts[j], checkPts[j+1])) error("self-intersecting polygon");
}
}
Решение
Я не уверен, что понял, потому что у вас, похоже, уже есть решение. Просто позвони lineIntersects на каждой паре несмежных ребер.
Если два ребра не имеют общих точек, то lineIntersects возвращает false, что ожидается.
Если два ребра пересекаются друг с другом, lineIntersects возвращает true, и, таким образом, вы знаете, что многоугольник не является слабо простым.
Если два ребра соприкасаются, как на картинке, то определитель, который вы вычисляете в linesIntersects, равен 0 (т.е. линии параллельны). lineIntersects возвращает ложь Что вам нужно (вы позволяете краям соприкасаться)
Конечно, всегда есть сложная часть, где операции с плавающей точкой приводят к ошибкам округления, но для меня математика в вашей функции верна. (и обязательно должен работать над примером на картинке)
Изменить: более «математический» подход. Два ребра имеют либо 0 общих точек, 1 общую точку, либо бесконечное количество общих точек (они «соприкасаются»). Быть слабо простым означает, что для любых двух пар ребер вам не разрешено иметь дело «1 точка в общем». Таким образом, вам нужна функция, которая обнаруживает, когда у вас есть ровно 1 общая точка. Я утверждаю, что lineIntersects уже делает это
Изменить 2: я забыл объяснить, что наличие 1 точки общего не всегда проблема. Но только если общая точка между двумя ребрами находится в конечной точке одного из двух ребер. Тогда мы должны «разрешить» это (вернуть false). Но это не меняет мой ответ, потому что в lineIntersectsмы вычисляем s < 1. && s > 0. && t < 1. && t > 0. и не s <= 1. && s >= 0. && t <= 1. && t >= 0., Так что мы уже «разрешаем» этот случай.
Другие решения
