Простое объяснение алгоритма быстрого показателя Анкерля

Недавно я искал более быструю альтернативу математической функции exp (x). Я нашел что-то, что мне очень понравилось, чаще всего это решение называется алгоритмом Анкерля. Ссылки:

https://github.com/ekmett/approximate/blob/master/cbits/fast.c
https://martin.ankerl.com/2012/01/25/optimized-approximative-pow-in-c-and-cpp/

Есть типичный анкерл exp реализация функции на C

double exp_fast(double a)
{
union { double d; long long x; } u;
u.x = (long long)(6497320848556798LL * a + 0x3fef127e83d16f12LL);
return u.d;
}

int main()
{
for (float x = 0; x < 10; x += 0.01)
std::cout << x << '\t'
<< exp(x) << '\t'
<< exp_fast(x)
<< std::endl;

return 0;
}

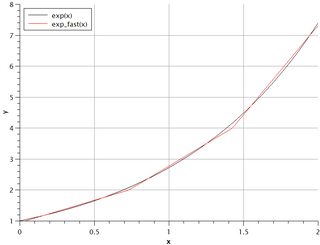
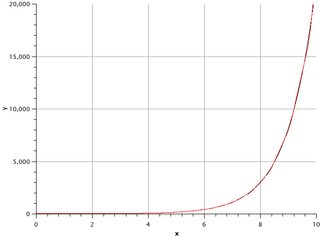
К сожалению, я не смог найти описание этого алгоритма. Возможно, в литературе это называется чем-то другим. Я попытался построить эту функцию и был очень удивлен — это кусочно-линейное приближение функции экспоненты! Он отлично работает в очень широком диапазоне выходных значений. Все графики содержат около тысячи точек (нажмите, чтобы увеличить)

Я не мог понять, как именно это работает, несмотря на все усилия. Меня удивляет, как такой простой код может дать такое хорошее приближение. Я буду очень признателен, если кто-то может четко объяснить, как это работает и из каких соображений ценности 6497320848556798LL, 0x3fef127e83d16f12LL выбраны. И второе — безопасно ли использовать такое решение или это своего рода грязный взлом, которого следует избегать?