Пропускать списки, они действительно так же хороши, как претензии Пью?
Я пытаюсь реализовать список пропусков, который работает так же хорошо, как BST, используя минимальные дополнительные затраты памяти, в настоящий момент, даже не принимая во внимание какие-либо ограничения памяти, производительность моей реализации SkipList далека от даже очень наивной сбалансированной реализации BST — так сказать, БТС ручной работы 🙂 —
В качестве ссылки я использую оригинальную статью Уильяма Пью PUG89 и реализация, которую я нашел в Алгоритмах в C от Sedgewick -13.5-. Мой код является рекурсивной реализацией, вот подсказка операции вставки и поиска:
sl_node* create_node()
{
short lvl {1};
while((dist2(en)<p)&&(lvl<max_level))
++lvl;
return new sl_node(lvl);
}
void insert_impl(sl_node* cur_node,
sl_node* new_node,
short lvl)
{
if(cur_node->next_node[lvl]==nullptr || cur_node->next_node[lvl]->value > new_node->value){
if(lvl<new_node->lvl){
new_node->next_node[lvl] = cur_node->next_node[lvl];
cur_node->next_node[lvl] = new_node;
}
if(lvl==0) return;
insert_impl(cur_node,new_node,lvl-1);
return;
}
insert_impl(cur_node->next_node[lvl],new_node,lvl);
}
sl_node* insert(long p_val)
{
sl_node* new_node = create_node();
new_node->value = p_val;
insert_impl(head, new_node,max_level-1);
return new_node;
}
И это код для операции поиска:
sl_node* find_impl(sl_node* cur_node,
long p_val,
int lvl)
{
if(cur_node==nullptr) return nullptr;
if(cur_node->value==p_val) return cur_node;
if(cur_node->next_node[lvl] == nullptr || cur_node->next_node[lvl]->value>p_val){
if(lvl==0) return nullptr;
return find_impl(cur_node,p_val,lvl-1);
}
return find_impl(cur_node->next_node[lvl],p_val,lvl);
}
sl_node* find(long p_val)
{
return find_impl(head,p_val,max_level-1);
}
Узел списка sl_node -skip выглядит следующим образом:
struct sl_node
{
long value;
short lvl;
sl_node** next_node;
sl_node(int l) : lvl(l)
{
next_node = new sl_node*[l];
for(short i{0};i<l;i++)
next_node[i]=nullptr;
}
~sl_node()
{
delete[] next_node;
}
};
Как вы можете видеть, в реализации нет ничего особенного или продвинутого по сравнению с книжной реализацией, я не буду делиться кодом Balaced BTS, так как не думаю, что здесь нужен, но это очень базовая BTS с функцией ребалансировки, срабатывающей во время вставка, когда высота нового узла больше 16 * lg (n), где n — количество узлов.
Скажем так, я перебалансировал три, только если максимальная высота в 16 раз больше, чем лучшая теоретическая, как я уже сказал, этот простой домашний BST работает намного лучше, чем домашний Skip List.
Но сначала давайте посмотрим на некоторые данные, используя p = .5 и n = 262144, уровень узлов в SkipList имеет следующее распределение:
1:141439, 53.9547%
2:65153, 24.8539%
3:30119, 11.4895%
4:13703, 5.22728%
5:6363, 2.42729%
6:2895, 1.10435%
7:1374, 0.524139%
8:581, 0.221634%
9:283, 0.107956%
10:117, 0.044632%
11:64, 0.0244141%
12:31, 0.0118256%
13:11, 0.00419617%
14:5, 0.00190735%
15:1, 0.00038147%
16:5, 0.00190735%
Который почти идеально — о, это большой! — соответствует теории из статьи, то есть: 50% уровня 1, 25% уровня 2 и так далее, и так далее. Входные данные были получены из моего лучшего генератора псевдослучайных чисел, известного как std :: random_device с std :: default_random_engine и равномерным распределением int. Вход выглядит довольно случайным для меня :)!
Время, необходимое для поиска «всех» элементов 262144 в SkipList — в случайном порядке — составляет 315 мс на моем компьютере, тогда как для той же операции поиска на наивной BTS требуемое время составляет 134 мс, поэтому BTS почти в два раза быстрее, чем SkipList. Это не совсем то, что я ожидал от «Алгоритмы пропуска списка имеют те же асимптотические ожидаемые границы времени, что и сбалансированные деревья, и они просты, быстрее и занимают меньше места» PUG89.
Время, необходимое для «вставки» узлов, составляет 387 мс для SkipList и 143 мс для BTS, опять же, наивный BST работает лучше.
Вещи становятся немного более интересными, если вместо использования случайной последовательности входного номера я использую отсортированную последовательность, здесь мой плохой самодельный BST становится медленным, и вставка 262144 отсортированных int занимает 2866 мс, тогда как SkipList требует только 168 мс.
Но, когда приходит время поиска, BST все еще быстрее! для отсортированного ввода мы имеем 234 мс против 77 мс, этот BST в 3 раза быстрее.
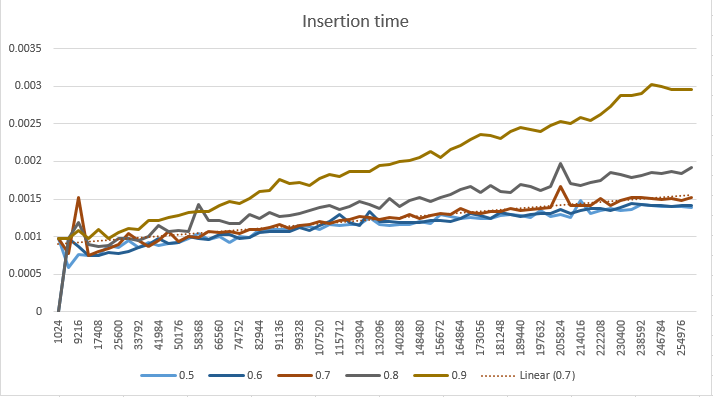
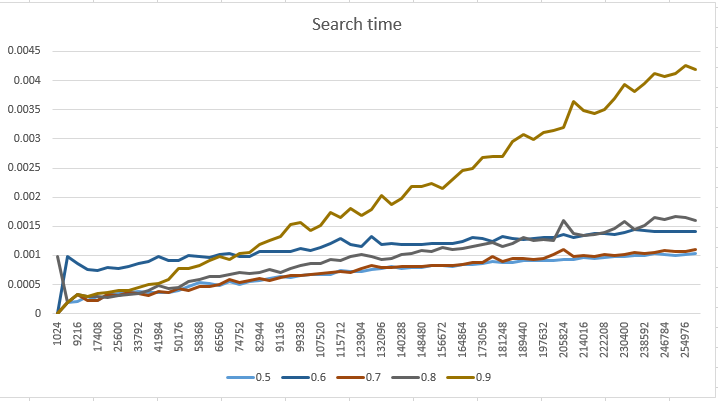
При разных значениях p-фактора я получил несколько иные результаты производительности:
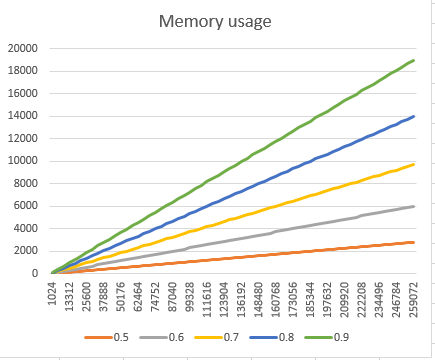
И, наконец, что не менее важно, график использования памяти, который, как вы можете ожидать, подтверждает, что если мы увеличим количество уровней на узел, мы существенно повлияем на отпечаток памяти. Использование памяти рассчитывается как сумма пространства, необходимого для хранения дополнительных указателей для всех узлов.
После всего этого, кто-нибудь из вас может дать мне комментарий о том, как реализовать SkipList, работающий так же хорошо, как BTS — не считая дополнительной памяти -?
Я знаю о статье от DrDobbs ССЫЛКА НА САЙТ о SkipList, и я прошел через все бумаги, код для операции поиска и вставки точно соответствует исходной реализации из PUG89 так должно быть так же хорошо, как у меня, и статья не дает никакого анализа производительности в любом случае, я не нашел другого источника. Вы можете мне помочь?
Любой комментарий высоко ценится!
Спасибо! 🙂
Решение
история
Времена немного изменились с тех пор, как Уильям Пью написал свою оригинальную статью. Мы не видим упоминаний в его статье об иерархии памяти ЦП и операционной системы, которая сегодня стала столь распространенной (сейчас часто столь же важной, как и сложность алгоритмов).
Его входной пример для бенчмаркинга содержал жалкие 2 ^ 16 элементов, а в то время аппаратное обеспечение обычно имело максимум 32-разрядную доступную адресацию памяти. Это сделало размер указателя вдвое меньше или меньше, чем мы привыкли сегодня на 64-битных машинах. Между тем, строковое поле, например, может быть таким же большим, что делает отношение между элементами, хранящимися в списке пропуска, и указателями, требуемыми для пропускаемого узла, потенциально намного меньшим, особенно учитывая, что нам часто требуется количество указателей на узел пропуска ,
Компиляторы C не были такими агрессивными в оптимизации в отношении таких вещей, как распределение регистров и выбор инструкций. Даже обычная рукописная сборка часто может обеспечить значительное преимущество в производительности. Компилятор намекает как register а также inline на самом деле сделал большое дело в те времена. Хотя это может показаться спорным, поскольку и сбалансированная реализация BST, и реализация списка пропусков будут здесь на равных, оптимизация даже базового цикла была более ручным процессом. Когда оптимизация становится все более ручным процессом, что-то, что легче реализовать, часто легче оптимизировать. Часто считается, что списки пропусков гораздо проще реализовать, чем балансирующее дерево.
Таким образом, все эти факторы, вероятно, были частью выводов Пью в то время. Однако времена изменились: изменилось оборудование, изменились операционные системы, изменились компиляторы, были проведены дополнительные исследования по этим темам и т. Д.
Реализация
Если оставить в стороне, давайте повеселимся и реализуем простой список пропусков. В итоге я адаптировал доступную реализацию Вот из лени. Это заурядная реализация, едва ли отличающаяся от множества легкодоступных примерных реализаций списка пропусков, существующих сегодня.
Мы будем сравнивать производительность нашей реализации с std::set который почти всегда реализуется как красно-черное дерево *.
* Некоторые могут задаться вопросом, почему я использую 0 вместо nullptr и тому подобное. Это привычка. На моем рабочем месте нам все еще приходится писать открытые библиотеки, предназначенные для широкого спектра компиляторов, включая те, которые поддерживают только C ++ 03, поэтому я все еще привык писать таким образом код реализации более низкого / среднего уровня, а иногда даже в C, поэтому, пожалуйста, прости старый стиль, в котором я написал этот код.
#include <iostream>
#include <algorithm>
#include <cstdlib>
#include <ctime>
#include <cmath>
#include <vector>
#include <cassert>
#include <cstring>
#include <set>
using namespace std;
static const int max_level = 32;
static const float probability = 0.5;
static double sys_time()
{
return static_cast<double>(clock()) / CLOCKS_PER_SEC;
}
static int random_level()
{
int lvl = 1;
while ((static_cast<float>(rand()) / RAND_MAX) < probability && lvl < max_level)
++lvl;
return lvl;
}
template <class T>
class SkipSet
{
public:
SkipSet(): head(0)
{
head = create_node(max_level, T());
level = 0;
}
~SkipSet()
{
while (head)
{
Node* to_destroy = head;
head = head->next[0];
destroy_node(to_destroy);
}
}
bool contains(const T& value) const
{
const Node* node = head;
for (int i=level; i >= 0; --i)
{
while (node->next[i] && node->next[i]->value < value)
node = node->next[i];
}
node = node->next[0];
return node && node->value == value;
}
void insert(const T& value)
{
Node* node = head;
Node* update[max_level + 1];
memset(update, 0, sizeof(Node*)*(max_level + 1));
for (int i = level; i >= 0; i--)
{
while (node->next[i] && node->next[i]->value < value)
node = node->next[i];
update[i] = node;
}
node = node->next[0];
if (!node || node->value != value)
{
int lvl = random_level();
assert(lvl >= 0);
if (lvl > level)
{
for (int i = level + 1; i <= lvl; i++) {
update[i] = head;
}
level = lvl;
}
node = create_node(lvl, value);
for (int i = 0; i <= lvl; i++) {
node->next[i] = update[i]->next[i];
update[i]->next[i] = node;
}
}
}
bool erase(const T& value)
{
Node* node = head;
Node* update[max_level + 1];
memset(update, 0, sizeof(Node*)*(max_level + 1));
for (int i = level; i >= 0; i--)
{
while (node->next[i] && node->next[i]->value < value)
node = node->next[i];
update[i] = node;
}
node = node->next[0];
if (node->value == value)
{
for (int i = 0; i <= level; i++) {
if (update[i]->next[i] != node)
break;
update[i]->next[i] = node->next[i];
}
destroy_node(node);
while (level > 0 && !head->next[level])
--level;
return true;
}
return false;
}
private:
struct Node
{
T value;
struct Node** next;
};
Node* create_node(int level, const T& new_value)
{
void* node_mem = malloc(sizeof(Node));
Node* new_node = static_cast<Node*>(node_mem);
new (&new_node->value) T(new_value);
void* next_mem = calloc(level+1, sizeof(Node*));
new_node->next = static_cast<Node**>(next_mem);
return new_node;
}
void destroy_node(Node* node)
{
node->value.~T();
free(node->next);
free(node);
}
Node* head;
int level;
};
template <class T>
bool contains(const std::set<T>& cont, const T& val)
{
return cont.find(val) != cont.end();
}
template <class T>
bool contains(const SkipSet<T>& cont, const T& val)
{
return cont.contains(val);
}
template <class Set, class T>
void benchmark(int num, const T* elements, const T* search_elements)
{
const double start_insert = sys_time();
Set element_set;
for (int j=0; j < num; ++j)
element_set.insert(elements[j]);
cout << "-- Inserted " << num << " elements in " << (sys_time() - start_insert) << " secs" << endl;
const double start_search = sys_time();
int num_found = 0;
for (int j=0; j < num; ++j)
{
if (contains(element_set, search_elements[j]))
++num_found;
}
cout << "-- Found " << num_found << " elements in " << (sys_time() - start_search) << " secs" << endl;
const double start_erase = sys_time();
int num_erased = 0;
for (int j=0; j < num; ++j)
{
if (element_set.erase(search_elements[j]))
++num_erased;
}
cout << "-- Erased " << num_found << " elements in " << (sys_time() - start_erase) << " secs" << endl;
}
int main()
{
const int num_elements = 200000;
vector<int> elements(num_elements);
for (int j=0; j < num_elements; ++j)
elements[j] = j;
random_shuffle(elements.begin(), elements.end());
vector<int> search_elements = elements;
random_shuffle(search_elements.begin(), search_elements.end());
typedef std::set<int> Set1;
typedef SkipSet<int> Set2;
for (int j=0; j < 3; ++j)
{
cout << "std::set" << endl;
benchmark<Set1>(num_elements, &elements[0], &search_elements[0]);
cout << endl;
cout << "SkipSet" << endl;
benchmark<Set2>(num_elements, &elements[0], &search_elements[0]);
cout << endl;
}
}
На GCC 5.2, -O2 я получаю это:
std::set
-- Inserted 200000 elements in 0.104869 secs
-- Found 200000 elements in 0.078351 secs
-- Erased 200000 elements in 0.098208 secs
SkipSet
-- Inserted 200000 elements in 0.188765 secs
-- Found 200000 elements in 0.160895 secs
-- Erased 200000 elements in 0.162444 secs
… что довольно ужасно Мы почти вдвое медленнее по всем направлениям.
оптимизация
Тем не менее, мы можем сделать явную оптимизацию. Если мы посмотрим на Node, его текущие поля выглядят так:
struct Node
{
T value;
struct Node** next;
};
Это подразумевает, что память для полей Node и список следующих указателей представляют собой два отдельных блока, возможно, с очень отдаленным шагом между ними, вот так:
[Node fields]-------------------->[next0,next1,...,null]
Это плохо влияет на местность ссылки. Если мы хотим улучшить ситуацию здесь, мы должны объединить эти блоки памяти в единую непрерывную структуру, например, так:
[Node fields,next0,next1,...,null]
Мы можем добиться этого с помощью структурной идиомы с переменной длиной, распространенной в C. Это немного неудобно для реализации в C ++, которая не поддерживает его напрямую, но мы можем эмулировать эффект следующим образом:
struct Node
{
T value;
struct Node* next[1];
};
Node* create_node(int level, const T& new_value)
{
void* node_mem = malloc(sizeof(Node) + level * sizeof(Node*));
Node* new_node = static_cast<Node*>(node_mem);
new (&new_node->value) T(new_value);
for (int j=0; j < level+1; ++j)
new_node->next[j] = 0;
return new_node;
}
void destroy_node(Node* node)
{
node->value.~T();
free(node);
}
С этой скромной настройкой у нас теперь есть такие времена:
SkipSet (Before)
-- Inserted 200000 elements in 0.188765 secs
-- Found 200000 elements in 0.160895 secs
-- Erased 200000 elements in 0.162444 secs
SkipSet (After)
-- Inserted 200000 elements in 0.132322 secs
-- Found 200000 elements in 0.127989 secs
-- Erased 200000 elements in 0.130889 secs
… что делает нас значительно ближе к соперничеству производительности std::set,
Генератор случайных чисел
Действительно эффективная реализация списка пропусков, как правило, требует очень быстрого ГСЧ. Тем не менее, во время сеанса быстрого профилирования я обнаружил, что на создание случайного уровня / высоты тратится лишь очень небольшая часть времени, чего едва ли достаточно, чтобы считать его горячей точкой. Это также повлияет только на время вставки, если оно не обеспечит более равномерное распределение, поэтому я решил пропустить эту оптимизацию.
Распределитель памяти
На данный момент, я бы сказал, у нас есть довольно разумный обзор того, что мы можем ожидать от реализации списка пропусков по сравнению с BST:
Insertion
-- std::set: 0.104869 secs
-- SkipList: 0.132322 secs
Search:
-- std::set: 0.078351 secs
-- SkipList: 0.127989 secs
Removal:
-- std::set: 0.098208 secs
-- SkipList: 0.130889 secs
Однако, если мы хотим продвинуться немного дальше, мы можем использовать фиксированный распределитель. На данный момент мы немного обманываем как std::set предназначен для работы с любым распределителем общего назначения, который соответствует требованиям интерфейса стандартного распределителя. Но давайте посмотрим на использование фиксированного распределителя:
#include <iostream>
#include <iomanip>
#include <algorithm>
#include <cstdlib>
#include <ctime>
#include <cmath>
#include <vector>
#include <cassert>
#include <set>
using namespace std;
static const int max_level = 32;
class FixedAlloc
{
public:
FixedAlloc(): root_block(0), free_element(0), type_size(0), block_size(0), block_num(0)
{
}
FixedAlloc(int itype_size, int iblock_size): root_block(0), free_element(0), type_size(0), block_size(0), block_num(0)
{
init(itype_size, iblock_size);
}
~FixedAlloc()
{
purge();
}
void init(int new_type_size, int new_block_size)
{
purge();
block_size = max(new_block_size, type_size);
type_size = max(new_type_size, static_cast<int>(sizeof(FreeElement)));
block_num = block_size / type_size;
}
void purge()
{
while (root_block)
{
Block* block = root_block;
root_block = root_block->next;
free(block);
}
free_element = 0;
}
void* allocate()
{
assert(type_size > 0);
if (free_element)
{
void* mem = free_element;
free_element = free_element->next_element;
return mem;
}
// Create new block.
void* new_block_mem = malloc(sizeof(Block) - 1 + type_size * block_num);
Block* new_block = static_cast<Block*>(new_block_mem);
new_block->next = root_block;
root_block = new_block;
// Push all but one of the new block's elements to the free pool.
char* mem = new_block->mem;
for (int j=1; j < block_num; ++j)
{
FreeElement* element = reinterpret_cast<FreeElement*>(mem + j * type_size);
element->next_element = free_element;
free_element = element;
}
return mem;
}
void deallocate(void* mem)
{
FreeElement* element = static_cast<FreeElement*>(mem);
element->next_element = free_element;
free_element = element;
}
void swap(FixedAlloc& other)
{
std::swap(free_element, other.free_element);
std::swap(root_block, other.root_block);
std::swap(type_size, other.type_size);
std::swap(block_size, other.block_size);
std::swap(block_num, other.block_num);
}
private:
struct Block
{
Block* next;
char mem[1];
};
struct FreeElement
{
struct FreeElement* next_element;
};
// Disable copying.
FixedAlloc(const FixedAlloc&);
FixedAlloc& operator=(const FixedAlloc&);
struct Block* root_block;
struct FreeElement* free_element;
int type_size;
int block_size;
int block_num;
};
static double sys_time()
{
return static_cast<double>(clock()) / CLOCKS_PER_SEC;
}
static int random_level()
{
int lvl = 1;
while (rand()%2 == 0 && lvl < max_level)
++lvl;
return lvl;
}
template <class T>
class SkipSet
{
public:
SkipSet(): head(0)
{
for (int j=0; j < max_level; ++j)
allocs[j].init(sizeof(Node) + (j+1)*sizeof(Node*), 4096);
head = create_node(max_level, T());
level = 0;
}
~SkipSet()
{
while (head)
{
Node* to_destroy = head;
head = head->next[0];
destroy_node(to_destroy);
}
}
bool contains(const T& value) const
{
const Node* node = head;
for (int i=level; i >= 0; --i)
{
while (node->next[i] && node->next[i]->value < value)
node = node->next[i];
}
node = node->next[0];
return node && node->value == value;
}
void insert(const T& value)
{
Node* node = head;
Node* update[max_level + 1] = {0};
for (int i=level; i >= 0; --i)
{
while (node->next[i] && node->next[i]->value < value)
node = node->next[i];
update[i] = node;
}
node = node->next[0];
if (!node || node->value != value)
{
const int lvl = random_level();
assert(lvl >= 0);
if (lvl > level)
{
for (int i = level + 1; i <= lvl; ++i)
update[i] = head;
level = lvl;
}
node = create_node(lvl, value);
for (int i = 0; i <= lvl; ++i)
{
node->next[i] = update[i]->next[i];
update[i]->next[i] = node;
}
}
}
bool erase(const T& value)
{
Node* node = head;
Node* update[max_level + 1] = {0};
for (int i=level; i >= 0; --i)
{
while (node->next[i] && node->next[i]->value < value)
node = node->next[i];
update[i] = node;
}
node = node->next[0];
if (node->value == value)
{
for (int i=0; i <= level; ++i) {
if (update[i]->next[i] != node)
break;
update[i]->next[i] = node->next[i];
}
destroy_node(node);
while (level > 0 && !head->next[level])
--level;
return true;
}
return false;
}
void swap(SkipSet<T>& other)
{
for (int j=0; j < max_level; ++j)
allocs[j].swap(other.allocs[j]);
std::swap(head, other.head);
std::swap(level, other.level);
}
private:
struct Node
{
T value;
int num;
struct Node* next[1];
};
Node* create_node(int level, const T& new_value)
{
void* node_mem = allocs[level-1].allocate();
Node* new_node = static_cast<Node*>(node_mem);
new (&new_node->value) T(new_value);
new_node->num = level;
for (int j=0; j < level+1; ++j)
new_node->next[j] = 0;
return new_node;
}
void destroy_node(Node* node)
{
node->value.~T();
allocs[node->num-1].deallocate(node);
}
FixedAlloc allocs[max_level];
Node* head;
int level;
};
template <class T>
bool contains(const std::set<T>& cont, const T& val)
{
return cont.find(val) != cont.end();
}
template <class T>
bool contains(const SkipSet<T>& cont, const T& val)
{
return cont.contains(val);
}
template <class Set, class T>
void benchmark(int num, const T* elements, const T* search_elements)
{
const double start_insert = sys_time();
Set element_set;
for (int j=0; j < num; ++j)
element_set.insert(elements[j]);
cout << "-- Inserted " << num << " elements in " << (sys_time() - start_insert) << " secs" << endl;
const double start_search = sys_time();
int num_found = 0;
for (int j=0; j < num; ++j)
{
if (contains(element_set, search_elements[j]))
++num_found;
}
cout << "-- Found " << num_found << " elements in " << (sys_time() - start_search) << " secs" << endl;
const double start_erase = sys_time();
int num_erased = 0;
for (int j=0; j < num; ++j)
{
if (element_set.erase(search_elements[j]))
++num_erased;
}
cout << "-- Erased " << num_found << " elements in " << (sys_time() - start_erase) << " secs" << endl;
}
int main()
{
const int num_elements = 200000;
vector<int> elements(num_elements);
for (int j=0; j < num_elements; ++j)
elements[j] = j;
random_shuffle(elements.begin(), elements.end());
vector<int> search_elements = elements;
random_shuffle(search_elements.begin(), search_elements.end());
typedef std::set<int> Set1;
typedef SkipSet<int> Set2;
cout << fixed << setprecision(3);
for (int j=0; j < 2; ++j)
{
cout << "std::set" << endl;
benchmark<Set1>(num_elements, &elements[0], &search_elements[0]);
cout << endl;
cout << "SkipSet" << endl;
benchmark<Set2>(num_elements, &elements[0], &search_elements[0]);
cout << endl;
}
}
* Я также внес небольшую поправку в random_level чтобы сделать это просто принять вероятность 50% после обнаружения, что это, кажется, работает довольно хорошо.
Используя фиксированный распределитель, мы можем быстро распределять и освобождать элементы, используя очень простую стратегию с постоянным временем, и, что более важно, распределять узлы таким образом, чтобы узлы с одинаковой высотой (наиболее часто используемые вместе) распределялись более последовательно с уважение друг к другу (хотя и не в идеальном последовательном порядке). Это улучшает время, чтобы:
Insertion
-- std::set: 0.104869 secs
-- SkipList: 0.103632 secs
Search:
-- std::set: 0.078351 secs
-- SkipList: 0.089910 secs
Removal:
-- std::set: 0.098208 secs
-- SkipList: 0.089224 secs
… что неплохо за 40 минут работы против std::set который был ткнул и подталкивал и настраивал эксперты по всей отрасли. У нас также есть более быстрые удаления, чем std::set (время вставки немного колеблется на моей машине, я бы сказал, что они примерно на одном уровне).
Конечно, мы обманули, чтобы применить этот последний шаг. Использование специального распределителя изменяет положение в нашу пользу, а также изменяет характеристики контейнера таким образом, что его память не может быть освобождена до тех пор, пока он не будет очищен, уничтожен или уплотнен. Он может пометить память как неиспользуемую и восстановить ее при последующих вставках, но не может сделать доступной память доступную для тех, кто находится вне списка пропуска. Я также не удосужился обратить внимание на правильное выравнивание для всех возможных типов T что было бы необходимо, чтобы действительно обобщить это.
Сортированный вход
Давайте попробуем использовать это против отсортированного ввода. Для этого просто закомментируйте два random_shuffle заявления. На моем конце я теперь получаю эти времена:
std::set
-- Inserted 200000 elements in 0.044 secs
-- Found 200000 elements in 0.023 secs
-- Erased 200000 elements in 0.019 secs
SkipSet
-- Inserted 200000 elements in 0.027 secs
-- Found 200000 elements in 0.023 secs
-- Erased 200000 elements in 0.016 secs
… а теперь наш SkipSet Превосходит std::set во всех областях, хотя только для этого одного исключительного случая.
Заключение
Так что я не знаю точно, что это говорит о пропуске списков. Едва потратив время и силы, мы приблизились к соперничеству. std::set*. Тем не менее, мы не победили, и нам пришлось обманывать с распределителем памяти, чтобы быть действительно близко.
* Обратите внимание, что пробег может варьироваться в зависимости от машины, реализации поставщика std::set, так далее.
Времена немного изменились с тех пор, как Пью написал в 1989 году.
Сегодня преимущества локальности ссылок преобладают до такой степени, что даже алгоритм линейной сложности может превзойти линейный алгоритм при условии, что первый значительно лучше кеширует или удобен для страниц. Уделение пристального внимания тому, как система захватывает куски памяти с верхних уровней иерархии памяти (например, вторичной ступени) с более медленной, но большей памятью и вплоть до маленькой строки кэша L1 и маленького регистра, является более значительным делом, чем когда-либо прежде, и больше не «микро», если вы спросите меня, когда преимущества могут конкурировать с алгоритмическими улучшениями.
Список пропусков здесь потенциально урезан, учитывая значительно больший размер узлов и, что не менее важно, переменный размер узлов (что затрудняет их очень эффективное распределение).
Одна вещь, на которую мы не смотрели, это локализованная природа, в которой пропускаемый список обновляется при вставке. Это имеет тенденцию влиять на гораздо меньшее количество областей, чем требуется для балансировки дерева, чтобы перебалансировать путем вращения родительских узлов. В результате, список пропусков может предложить потенциально более эффективную реализацию параллельного набора или карты.
Еще одна многообещающая характеристика пропускаемого списка — это просто связанный список на самом низком уровне. В результате он предлагает очень простой последовательный обход по линейному времени без необходимости спускаться вниз по ветвям дерева с линейной сложностью, поэтому потенциально очень хорошо, если мы хотим выполнить много итераций по линейному времени через все содержащиеся в нем элементы. ,
Но всегда помните:
Техника настолько хороша, насколько ее можно применить в руках разработчика.
Другие решения
Я сомневаюсь, что список пропусков был лучшим выбором, чем, например, дерево AVL даже в 1989 году. В 1989 или 1990 году, будучи студентом, я реализовал и то, и другое: это не была хорошая реализация списка пропусков, должен признать, я был новичком в то время.
Однако дерево AVL стало более сложным для реализации.
В отличие от этого, у меня были трудности с указателями впереди переменной длины с пропуском в списке, реализуемым в модуле 2, который я примитивей решал, всегда используя максимум 16 следующих указателей.
Преимущества меньшего количества операций при вставке я никогда не видел. Дерево AVL, если я правильно помню, в среднем занимало не более 2-3 операций. Так что дорогая перебалансировка происходит не часто.
Я думаю, что это было больше шумиха.