Применяя Kiss FFT к аудиосэмплам и получая выход NaN?
Название объясняет мою проблему.
То, что я пытаюсь сделать, довольно просто:
- Загрузить дорожку MP3 (через libmpg123)
- Читать образцы
- Применить Kiss FFT на образцы
Что я пробовал до сих пор
inline float scale(kiss_fft_scalar val)
{
int g = 0;
return val < 0 ? val*(1/32768.0f ) : val*(1/32767.0f);
}
void main()
{
mpg123_handle *m = NULL;
int channels = 0, encoding = 0;
long rate = 0;
int err = MPG123_OK;
err = mpg123_init();
m = mpg123_new(NULL, &err);
mpg123_open(m, "L:\\audio-io\\audio-analysis\\samples\\zero.mp3");
mpg123_getformat(m, &rate, &channels, &encoding);
err = mpg123_format_none(m);
err = mpg123_format(m, rate, channels, encoding);
// Get 2048 samples
const int TIME = 2048;
// 16-bit integer encoded in bytes, hence x2 size
unsigned char* buffer = new unsigned char[TIME*2];
size_t done = 0;
err = mpg123_read(m, buffer, TIME*2, &done);
short* samples = new short[done/2];
int index = 0;
// Iterate 2 bytes at a time
for (int i = 0; i < done; i += 2)
{
unsigned char first = buffer[i];
unsigned char second = buffer[i + 1];
samples[index++] = (first | (second << 8));
}
// Array to store the calculated data
int speclen = TIME / 2 + 1;
float* output = new float[speclen];
kiss_fftr_cfg config;
kiss_fft_cpx* spectrum;
config = kiss_fftr_alloc(TIME, 0, NULL, NULL);
spectrum = (kiss_fft_cpx*) malloc(sizeof(kiss_fft_cpx) * TIME);
// Right here...
kiss_fftr(config, (kiss_fft_scalar*) samples, spectrum);
for (int i = 0; i < speclen; i++)
{
float re = scale(spectrum[i].r) * TIME;
float im = scale(spectrum[i].i) * TIME;
output[i] = sqrtf(re*re + im*im);
}
return;
}
Проблема возникает на этой линии kiss_fftr(config, (kiss_fft_scalar*) samples, spectrum);
куда samples содержит образцы аудио (16 бит), и spectrum Предполагается, что для хранения выходных данных.
После завершения функции вот что происходит в окне отладчика.
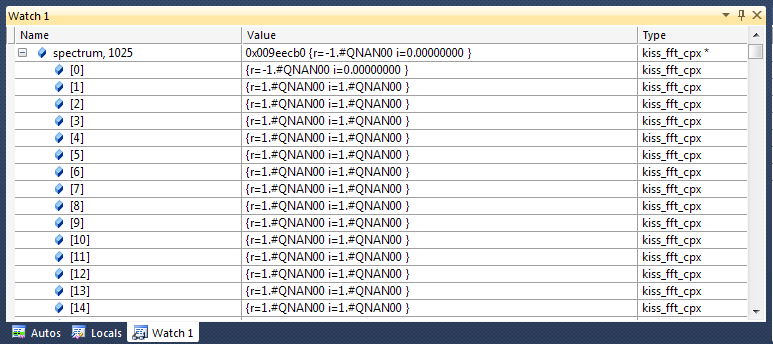
Может кто-нибудь дать мне простой пример того, как применять функции Kiss FFT к аудио (16-битным) семплам?
Решение
Вам нужно найти ошибки в вашем коде. Мой тестовый код работает нормально.
Комплексное форвардное БПФ с поплавками:
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#include "kiss_fft.h"
#ifndef M_PI
#define M_PI 3.14159265358979324
#endif
#define N 16
void TestFft(const char* title, const kiss_fft_cpx in[N], kiss_fft_cpx out[N])
{
kiss_fft_cfg cfg;
printf("%s\n", title);
if ((cfg = kiss_fft_alloc(N, 0/*is_inverse_fft*/, NULL, NULL)) != NULL)
{
size_t i;
kiss_fft(cfg, in, out);
free(cfg);
for (i = 0; i < N; i++)
printf(" in[%2zu] = %+f , %+f ""out[%2zu] = %+f , %+f\n",
i, in[i].r, in[i].i,
i, out[i].r, out[i].i);
}
else
{
printf("not enough memory?\n");
exit(-1);
}
}
int main(void)
{
kiss_fft_cpx in[N], out[N];
size_t i;
for (i = 0; i < N; i++)
in[i].r = in[i].i = 0;
TestFft("Zeroes (complex)", in, out);
for (i = 0; i < N; i++)
in[i].r = 1, in[i].i = 0;
TestFft("Ones (complex)", in, out);
for (i = 0; i < N; i++)
in[i].r = sin(2 * M_PI * 4 * i / N), in[i].i = 0;
TestFft("SineWave (complex)", in, out);
return 0;
}
Выход:
Zeroes (complex)
in[ 0] = +0.000000 , +0.000000 out[ 0] = +0.000000 , +0.000000
in[ 1] = +0.000000 , +0.000000 out[ 1] = +0.000000 , +0.000000
in[ 2] = +0.000000 , +0.000000 out[ 2] = +0.000000 , +0.000000
in[ 3] = +0.000000 , +0.000000 out[ 3] = +0.000000 , +0.000000
in[ 4] = +0.000000 , +0.000000 out[ 4] = +0.000000 , +0.000000
in[ 5] = +0.000000 , +0.000000 out[ 5] = +0.000000 , +0.000000
in[ 6] = +0.000000 , +0.000000 out[ 6] = +0.000000 , +0.000000
in[ 7] = +0.000000 , +0.000000 out[ 7] = +0.000000 , +0.000000
in[ 8] = +0.000000 , +0.000000 out[ 8] = +0.000000 , +0.000000
in[ 9] = +0.000000 , +0.000000 out[ 9] = +0.000000 , +0.000000
in[10] = +0.000000 , +0.000000 out[10] = +0.000000 , +0.000000
in[11] = +0.000000 , +0.000000 out[11] = +0.000000 , +0.000000
in[12] = +0.000000 , +0.000000 out[12] = +0.000000 , +0.000000
in[13] = +0.000000 , +0.000000 out[13] = +0.000000 , +0.000000
in[14] = +0.000000 , +0.000000 out[14] = +0.000000 , +0.000000
in[15] = +0.000000 , +0.000000 out[15] = +0.000000 , +0.000000
Ones (complex)
in[ 0] = +1.000000 , +0.000000 out[ 0] = +16.000000 , +0.000000
in[ 1] = +1.000000 , +0.000000 out[ 1] = +0.000000 , +0.000000
in[ 2] = +1.000000 , +0.000000 out[ 2] = +0.000000 , +0.000000
in[ 3] = +1.000000 , +0.000000 out[ 3] = +0.000000 , +0.000000
in[ 4] = +1.000000 , +0.000000 out[ 4] = +0.000000 , +0.000000
in[ 5] = +1.000000 , +0.000000 out[ 5] = +0.000000 , +0.000000
in[ 6] = +1.000000 , +0.000000 out[ 6] = +0.000000 , +0.000000
in[ 7] = +1.000000 , +0.000000 out[ 7] = +0.000000 , +0.000000
in[ 8] = +1.000000 , +0.000000 out[ 8] = +0.000000 , +0.000000
in[ 9] = +1.000000 , +0.000000 out[ 9] = +0.000000 , +0.000000
in[10] = +1.000000 , +0.000000 out[10] = +0.000000 , +0.000000
in[11] = +1.000000 , +0.000000 out[11] = +0.000000 , +0.000000
in[12] = +1.000000 , +0.000000 out[12] = +0.000000 , +0.000000
in[13] = +1.000000 , +0.000000 out[13] = +0.000000 , +0.000000
in[14] = +1.000000 , +0.000000 out[14] = +0.000000 , +0.000000
in[15] = +1.000000 , +0.000000 out[15] = +0.000000 , +0.000000
SineWave (complex)
in[ 0] = +0.000000 , +0.000000 out[ 0] = +0.000000 , +0.000000
in[ 1] = +1.000000 , +0.000000 out[ 1] = +0.000000 , +0.000000
in[ 2] = +0.000000 , +0.000000 out[ 2] = +0.000000 , +0.000000
in[ 3] = -1.000000 , +0.000000 out[ 3] = +0.000000 , +0.000000
in[ 4] = +0.000000 , +0.000000 out[ 4] = +0.000000 , -8.000000
in[ 5] = +1.000000 , +0.000000 out[ 5] = +0.000000 , +0.000000
in[ 6] = +0.000000 , +0.000000 out[ 6] = +0.000000 , +0.000000
in[ 7] = -1.000000 , +0.000000 out[ 7] = +0.000000 , +0.000000
in[ 8] = +0.000000 , +0.000000 out[ 8] = +0.000000 , +0.000000
in[ 9] = +1.000000 , +0.000000 out[ 9] = +0.000000 , +0.000000
in[10] = +0.000000 , +0.000000 out[10] = +0.000000 , +0.000000
in[11] = -1.000000 , +0.000000 out[11] = +0.000000 , +0.000000
in[12] = +0.000000 , +0.000000 out[12] = +0.000000 , +8.000000
in[13] = +1.000000 , +0.000000 out[13] = +0.000000 , +0.000000
in[14] = +0.000000 , +0.000000 out[14] = +0.000000 , +0.000000
in[15] = -1.000000 , +0.000000 out[15] = +0.000000 , +0.000000
Реальный форвардный БПФ с поплавками:
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#include "kiss_fftr.h"
#ifndef M_PI
#define M_PI 3.14159265358979324
#endif
#define N 16
void TestFftReal(const char* title, const kiss_fft_scalar in[N], kiss_fft_cpx out[N / 2 + 1])
{
kiss_fftr_cfg cfg;
printf("%s\n", title);
if ((cfg = kiss_fftr_alloc(N, 0/*is_inverse_fft*/, NULL, NULL)) != NULL)
{
size_t i;
kiss_fftr(cfg, in, out);
free(cfg);
for (i = 0; i < N; i++)
{
printf(" in[%2zu] = %+f ",
i, in[i]);
if (i < N / 2 + 1)
printf("out[%2zu] = %+f , %+f",
i, out[i].r, out[i].i);
printf("\n");
}
}
else
{
printf("not enough memory?\n");
exit(-1);
}
}
int main(void)
{
kiss_fft_scalar in[N];
kiss_fft_cpx out[N / 2 + 1];
size_t i;
for (i = 0; i < N; i++)
in[i] = 0;
TestFftReal("Zeroes (real)", in, out);
for (i = 0; i < N; i++)
in[i] = 1;
TestFftReal("Ones (real)", in, out);
for (i = 0; i < N; i++)
in[i] = sin(2 * M_PI * 4 * i / N);
TestFftReal("SineWave (real)", in, out);
return 0;
}
Выход:
Zeroes (real)
in[ 0] = +0.000000 out[ 0] = +0.000000 , +0.000000
in[ 1] = +0.000000 out[ 1] = +0.000000 , +0.000000
in[ 2] = +0.000000 out[ 2] = +0.000000 , +0.000000
in[ 3] = +0.000000 out[ 3] = +0.000000 , +0.000000
in[ 4] = +0.000000 out[ 4] = +0.000000 , +0.000000
in[ 5] = +0.000000 out[ 5] = +0.000000 , +0.000000
in[ 6] = +0.000000 out[ 6] = +0.000000 , +0.000000
in[ 7] = +0.000000 out[ 7] = +0.000000 , +0.000000
in[ 8] = +0.000000 out[ 8] = +0.000000 , +0.000000
in[ 9] = +0.000000
in[10] = +0.000000
in[11] = +0.000000
in[12] = +0.000000
in[13] = +0.000000
in[14] = +0.000000
in[15] = +0.000000
Ones (real)
in[ 0] = +1.000000 out[ 0] = +16.000000 , +0.000000
in[ 1] = +1.000000 out[ 1] = +0.000000 , +0.000000
in[ 2] = +1.000000 out[ 2] = +0.000000 , +0.000000
in[ 3] = +1.000000 out[ 3] = +0.000000 , +0.000000
in[ 4] = +1.000000 out[ 4] = +0.000000 , +0.000000
in[ 5] = +1.000000 out[ 5] = +0.000000 , +0.000000
in[ 6] = +1.000000 out[ 6] = +0.000000 , +0.000000
in[ 7] = +1.000000 out[ 7] = +0.000000 , +0.000000
in[ 8] = +1.000000 out[ 8] = +0.000000 , +0.000000
in[ 9] = +1.000000
in[10] = +1.000000
in[11] = +1.000000
in[12] = +1.000000
in[13] = +1.000000
in[14] = +1.000000
in[15] = +1.000000
SineWave (real)
in[ 0] = +0.000000 out[ 0] = +0.000000 , +0.000000
in[ 1] = +1.000000 out[ 1] = +0.000000 , +0.000000
in[ 2] = +0.000000 out[ 2] = +0.000000 , +0.000000
in[ 3] = -1.000000 out[ 3] = +0.000000 , +0.000000
in[ 4] = +0.000000 out[ 4] = +0.000000 , -8.000000
in[ 5] = +1.000000 out[ 5] = +0.000000 , +0.000000
in[ 6] = +0.000000 out[ 6] = +0.000000 , +0.000000
in[ 7] = -1.000000 out[ 7] = +0.000000 , +0.000000
in[ 8] = +0.000000 out[ 8] = +0.000000 , +0.000000
in[ 9] = +1.000000
in[10] = +0.000000
in[11] = -1.000000
in[12] = +0.000000
in[13] = +1.000000
in[14] = +0.000000
in[15] = -1.000000
Другие решения
Когда я впервые начал смотреть на этот ответ, я продолжал задаваться вопросом, почему -8.0 возникала в мнимом компоненте, а не в реальной части. Когда я перечитал печатную статью о БПФ, я понял, что думаю о величине.
Поэтому я подправил ответ в Сложном коде, чтобы изменить printf следующим образом
for (i = 0; i < N; i++)
printf(" in[%02i]=%+f, %+f out[%02i]=%+f, %+f M[%02i]=%+f\n",
i, in[i].r, in[i].i,
i, out[i].r, out[i].i,
i, sqrt((out[i].r * out[i].r) + (out[i].i * out[i].i)));
Что дает ответ, показывающий величину также.
...
SineWave (complex)
in[00]=+0.000000, +0.000000 out[00]=+0.000000, +0.000000 M[00]=+0.000000
in[01]=+1.000000, +0.000000 out[01]=+0.000000, +0.000000 M[01]=+0.000000
in[02]=+0.000000, +0.000000 out[02]=+0.000000, +0.000000 M[02]=+0.000000
in[03]=-1.000000, +0.000000 out[03]=+0.000000, +0.000000 M[03]=+0.000000
in[04]=-0.000000, +0.000000 out[04]=-0.000000, -8.000000 M[04]=+8.000000
in[05]=+1.000000, +0.000000 out[05]=+0.000000, -0.000000 M[05]=+0.000000
in[06]=+0.000000, +0.000000 out[06]=+0.000000, -0.000000 M[06]=+0.000000
in[07]=-1.000000, +0.000000 out[07]=+0.000000, -0.000000 M[07]=+0.000000
in[08]=-0.000000, +0.000000 out[08]=+0.000000, +0.000000 M[08]=+0.000000
in[09]=+1.000000, +0.000000 out[09]=+0.000000, +0.000000 M[09]=+0.000000
in[10]=+0.000000, +0.000000 out[10]=+0.000000, +0.000000 M[10]=+0.000000
in[11]=-1.000000, +0.000000 out[11]=+0.000000, +0.000000 M[11]=+0.000000
in[12]=-0.000000, +0.000000 out[12]=-0.000000, +8.000000 M[12]=+8.000000
in[13]=+1.000000, +0.000000 out[13]=+0.000000, -0.000000 M[13]=+0.000000
in[14]=+0.000000, +0.000000 out[14]=+0.000000, -0.000000 M[14]=+0.000000
in[15]=-1.000000, +0.000000 out[15]=+0.000000, -0.000000 M[15]=+0.000000
Я также играл с изменением частоты в цикле for, который генерирует синусоидальную волну.
float freq;
...
freq = 6.0;
for (i = 0; i < N; i++)
in[i].r = sin(2 * M_PI * freq * i / N), in[i].i = 0;
И до тех пор, пока я оставался с коэффициентами, кратными 1,0, и при частоте Найквиста 16/2 = 8, результат довольно хорошо переключался с бина на бин. Конечно, установка частоты в дробные значения позволяет увидеть, как ее величина распределяется по бинам, и без применения функции управления окнами мы получаем утечку. Если вы все еще боретесь с БПФ, как я играю с кодом, подобным этому, где вы можете увидеть все результаты на одном экране некоторое время, и все начинает проясняться.
Наконец, спасибо Алексею за ответ, который помог мне начать работу с Kiss FFT.
Попробуй это:
in[i].r = sin(2 * M_PI * freq * (i / N*1.00)), in[i].i = 0;
