Представление полинома со связанными списками

Question

Представление полинома со связанными списками

Заранее спасибо.
Для моего класса C ++ мне поручено представлять полином, такой как (MyPoly= 7x^6*y^4 + 4x^4*y^5 - 8x^5*y^3 – 9x + 8) использование связанных списков и построение узла & Поли классы, чтобы помочь выразить это.

Я не знаю, как представить многочлен с X и Y в связанном списке.

У меня есть идея построить связанный список для представления полинома, как 7 6 4 -> 4 4 5 -> -8 5 3 ->-9 1 0 -> 8 0 0 ->NULL

Я новичок в этом, поэтому любой пример кода или псевдокод будет иметь большую помощь.

Попытка установки

Я придумал этот код здесь (отправная точка), но я думаю, что он будет работать только для одной переменной, а не двух (7x ^ 6 * … но не 7x ^ 6 * y ^ 4). Еще раз спасибо :).

1

c++class linked-list polynomials

Решение

Другие решения

Я думаю, что вы можете представлять полином с матрицей, а не связным списком или что-то.

   |X^0|x^1|x^2|x^3
---|---|---|---|---
y^0|   |   |   |
---|---|---|---|---
y^1|   |   |   |
---|---|---|---|---
y^2|   |   |   |
---|---|---|---|---
y^3|   |   |   |

В каждой ячейке вы должны хранить коэффициенты x ^ x ‘и y ^ y’. И вы можете определить операции проще.

Ты можешь использовать Boost.uBLAS для матричных операций.

0

Быстрое решение не очень чистое:

MyPoly = 7x ^ 6 * y ^ 4 + 4x ^ 4 * y ^ 5 — 8x ^ 5 * y ^ 3 — 9x + 8

#include <list>
class factor;
class polynomial{
public:
std::list<factor> factors;
};

class factor{
public:
factor()=default;
factor(int constant,int x_pow,int y_pow):constant(constant),x_pow(x_pow),y_pow(y_pow){}
int constant;
int x_pow;
int y_pow;

};
int main()
{
polynomial MyPoly;
MyPoly.factors.emplace_back(7,6,4);
MyPoly.factors.emplace_back(4,4,5);
MyPoly.factors.emplace_back(8,5,3);
MyPoly.factors.emplace_back(9,1,0);
MyPoly.factors.emplace_back(8,0,0);
}

0

Это был бы один из способов сделать это:

Особенности дизайна:
1. Рассмотрим полином как список узлов
2. Каждый узел может состоять из подузлов.

Итак, ваши определения классов будут:

class Polynomial
{
list<nodes> termList;
};

class Node
{
list<SubNodes> subnodelist;

};

template<class T>
class subNode
{
int coefficient;
int power;
T variable;
};

Примечание: не проверен код на правильность.

-1

Источник

Accepted Answer

Вы думали, или вам разрешено работать с Представление Хорнера многочленов? Это не только гораздо более эффективный способ вычисления полиномиальных значений, но во многих случаях это может привести к более разреженной структуре данных. Например, полином:

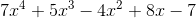
7x ^ 4 + 5x ^ 3-4x ^ 2 + 8x-7

эквивалентно следующему выражению:

(((7x + 5) х-4) х + 8) х-7

Итак, есть 3 вещи, на которые стоит обратить внимание:

На самом деле одна замечательная вещь этой схемы (хотя и не имеет прямого отношения к вашему вопросу) состоит в том, что ее расчет намного быстрее, так как вы экономите много умножений.
Индекс полинома напрямую зависит от длина выражения
Все элементы в выражении isomorph, независимо от степени. Это также верно для каждой арности.

Так что в этом счастливом случае выбранный мною полином может быть очень легко и эффективно сохранен как следующий список / массив:

[7, 5, 1, -4, 1, 8, 1, -7]

или, если хотите, в виде связанного списка [X_mult | сумма] номера:
[7 | 5] -> [1 | 4] -> [1 | 8] -> [1 | -7]

тогда как вы знаете, что элементы с четными индексами умножаются на x и добавляются к следующему элементу, схема довольно проста.

#include <iostream>
using namespace std;

int main()
{
// the x you want to calculate
int x = 1;
// the horner-representation of your polynom
int A[8] {7, 5, 1, -4, 1, 8, 1, -7};
int partial;
int result = 1;
// run calculations following horner-schema
for (int i = 0; i < 8; i++) {
if (i%2==0){
partial = A[i]*x; // this mult. is only needed at i=0
result *= partial;
} else{
partial = A[i];
result += partial;
}
}
cout << "x=" << x << ", p(x)=" << result << endl;
return 0;
}

Вопросы: Вы можете значительно улучшить его производительность и использование памяти, если подавите нечетные индексы и примете «1» как должное, сохранив первые 7 в другом месте. Кроме того, поскольку индекс напрямую зависит от длины списка, полиномы, такие как 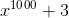будет иметь очень неэффективное представление.
Обойти проблемы с памятью: Возможный обходной путь — наследовать ваш ListElement как ExpandedListElement, чтобы числа в его контейнерах не интерпретировались как факторы, а как количество повторений. Таким образом, ExpandedListElement [1000 | a] будет означать, что в вашем списке есть тысяча ListElements, которые выглядят так: [1 | a]. Таким образом, данный пример x ^ 1000 + 3 будет иметь два элемента: ExpandedListElement [999 | 0] -> ListElement [1 | 3]. Вам также понадобится метод для выполнения цикла, который я опускаю (если вам нужен этот обходной путь, дайте мне знать, и я опубликую его).

Я не тестировал это подробно, но я предполагаю, что это хороший подход также для двух или более переменных. Я оставил также остальные детали ОО-реализации отдельно, но основные DS и операции есть и их должно быть легко внедрить в классы. Если вы попробуете, дайте мне знать, как это работает!

ура

Andres

1