Правило Буля для N интервалов (C)
Я пытаюсь реализовать правило Буля через n интервалов, используя эту формулу 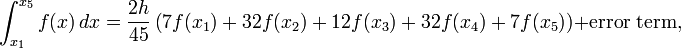
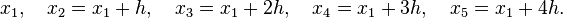
До сих пор я разработал этот код:
//f = function on the range [a,b] n = number of intervals
long double booles(long double (*f) (long double),
double a, double b, int n)
{
long double sum=7*f(a); //because the starting value is not doubled
long double h = (b - a)/(n-1); //width of each interval
int mod;
int i =1;
while (i<n-1)
{
mod = i%4;
if (mod==0)
sum+=14*f(a+i*h);
else if (mod==1)
sum+=32*f(a+i*h);
else if (mod==2)
sum+=12*f(a+i*h);
else
sum+=32*f(a+i*h);
++i;
}
return 2* h/45 * sum;
}
Это запустится и даст достойный ответ, но это не входит в правила ошибки Bool, которая гласит, что ошибка 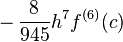 .
.
Я исправил проблему с удвоением первого слагаемого, но я не уверен, как исправить возможное удвоение в конце цикла. Кроме того, ошибка достаточно велика, поэтому я не думаю, что моя единственная проблема — это последние четыре условия.
Решение
-
длинный двойной
Вики говорит: тип с плавающей точкой повышенной точности. Фактические свойства не указаны. В отличие от типов float и double, это может быть 80-битный формат с плавающей запятой, не-IEEE «двойной-двойной» или IEEE 754 формат с плавающей запятой четвертой точности, если предоставляется формат с более высокой точностью, в противном случае он такой же, как двойной. См. Статью о длинном двойнике для деталей.
- поэтому трудно сказать, какой тип данных вы на самом деле используете (я предпочитаю использовать double)
-
константы
Вы смешиваете целые и плавающие числа, поэтому компилятор должен решить, что использовать. Переписать все плавающие числа как
45в45.0чтобы убедиться, что это сделано правильно илиa+i*h…iэто инт иhэто двойной … -
интеграция
не знаете величины суммы и диапазона ваших значений, но для повышения точности с плавающей точкой вам следует избегайте добавления больших и малых значений вместе потому что, если показатели слишком разные, вы теряете слишком много соответствующих битов мантиссы.
Сделайте сумму в двух переменных примерно так (в C ++):
double suml=0.0,sumh=0.0,summ=1000.0; for (int i=0;i<n;i++) { suml+=...; // here goes the formula if (fabs(suml)>summ) { sumh+=suml; suml=0; } } sumh+=suml; suml=0; // here the result is in sumh-
summмаксимальная величина suml. Это должно быть в относительно безопасном диапазоне по сравнению с вашим значением итерации суммы, например100-10000раз больше, чем среднее значение. -
sumlпеременная суммы малых величин sumhпеременная суммы больших величин
если диапазон ваших суммированных значений действительно большой, то вы можете добавить еще один, если
if (fabs(value)>summ) sumh+=value; else suml+=value;если он даже намного больше, то вы можете суммировать в любое количество переменных таким же образом, просто разделив диапазон значений на некоторые значения полных диапазонов
-
-
формула
может быть, я что-то упустил, но почему вы моддинг? Как я понимаю, вам не нужен цикл вообще, а также ifs устарели, так что зачем использовать
a+i*hи неa+=h? это улучшит производительность и точностьчто-то вроде этого:
double sum,h; h = (b-a)/double(n-1); sum = 7.0*f(a); a+=h; sum+=32.0*f(a); a+=h; sum+=12.0*f(a); a+=h; sum+=32.0*f(a); a+=h; sum+= 7.0*f(a); a+=h; return 2.0*h*sum/45.0; // + the thing in the bullet 3 of coarse ... // now I see you had an error in your constants !!!
[edit1] разделение реализовано (не в четыре раза)
//---------------------------------------------------------------------------
double f(double x)
{
// return x+0.2*x*x-0.001*x*x*x+2.0*cos(0.1*x)*tan(0.01*x*x)+25.0;
return x+0.2*x*x-0.001*x*x*x;
}
//---------------------------------------------------------------------------
double integrate_rect(double (*f)(double),double x0,double x1,int n)
{
int i;
double s=0.0,x=x0,dx=(x1-x0)/double(n-1);
for (i=0;i<n;i++,x+=dx) s+=f(x);
return s*dx;
}
//---------------------------------------------------------------------------
double integrate_Boole(double (*f)(double),double x0,double x1,int n)
{
n-=n%5; if (n<5) n=5;
int i;
double s=0.0,x=x0,dx=(x1-x0)/double(n-1);
for (i=0;i<n;i+=5)
{
s+= 7.0*f(x); x+=dx;
s+=32.0*f(x); x+=dx;
s+=12.0*f(x); x+=dx;
s+=32.0*f(x); x+=dx;
s+= 7.0*f(x); x+=dx;
}
s*=(2.0*dx)/(45.0);
return s*1.25; // this is the ratio to cover most cases
}
//---------------------------------------------------------------------------
void main()
{
int n=100000;
double x0=0.0,x1=+100.0,i0,i1;
i0=integrate_rect (f,x0,x1,n); cout << i0 << endl;
i1=integrate_Boole(f,x0,x1,n); cout << i1 << endl << i0/i1;
}
//---------------------------------------------------------------------------
Я использую в основном прямоугольное правило, потому что на FPU это самый быстрый и точный способ. Более продвинутые подходы лучше на бумаге, но на компьютере дополнительные накладные расходы и округление обычно медленнее / менее точны, чем та же точность с прямоугольным правилом
Другие решения
