Повернуть геометрию, чтобы выровнять вектор направления

Я пытался привести свою сгенерированную геометрию в соответствие с вектором направления. Чтобы проиллюстрировать мою текущую проблему:

• A = правильно выровненная геометрия (просто треугольник для тестирования)
• B = неправильно выровненная геометрия

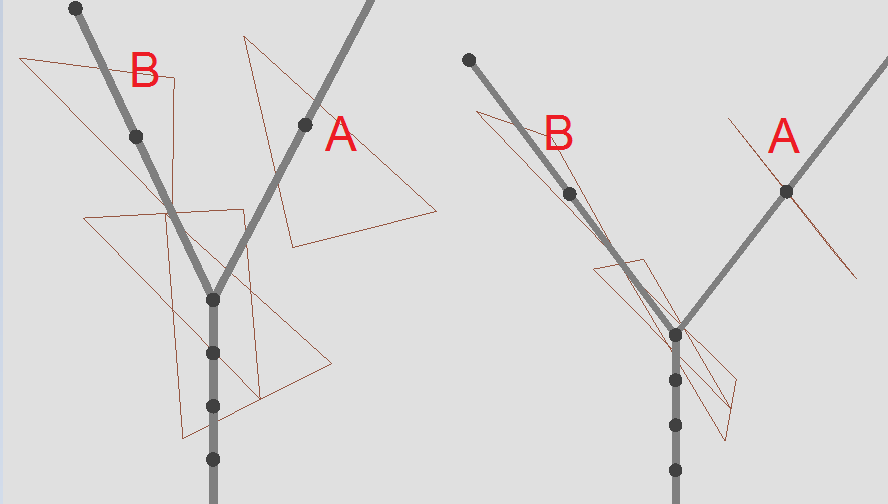
Мое текущее решение в коде для этого примера треугольника (этот код запускается для всех узлов, которые вы видите на экране, начиная с разделения, я использую математическую библиотеку GLM):

glm::vec3 v1, v2, v3;

v1.x = -0.25f;
v1.z = -0.25f;

v2.x = 0.25f;
v2.z = -0.25f;

v3.x = 0.0f;
v3.z = 0.25f;

v1.y = 0.0f;
v2.y = 0.0f;
v3.y = 0.0f;

glm::mat4x4 translate = glm::translate(glm::mat4x4(1.0f), sp.position);
glm::mat4x4 rotate = glm::lookAt(glm::vec3(0.0f, 0.0f, 0.0f), sp.direction, glm::vec3(0.0f, 1.0f, 0.0f));

v1 = glm::vec4(translate * rotate * glm::vec4(v1, 1.0f)).swizzle(glm::comp::X, glm::comp::Y, glm::comp::Z);
v2 = glm::vec4(translate * rotate * glm::vec4(v2, 1.0f)).swizzle(glm::comp::X, glm::comp::Y, glm::comp::Z);
v3 = glm::vec4(translate * rotate * glm::vec4(v3, 1.0f)).swizzle(glm::comp::X, glm::comp::Y, glm::comp::Z);

Значения вектора направления для точки A:

• х 0,000000000 плавать
• y 0.788205445 float
• z 0.615412235 float

Значения вектора направления для точки B:

• х 0.0543831661 плавать
• y 0.788205445 float
• z-0,613004684 float

Изменить 1 (24/11/2013 @ 20:36):
A и B не имеют никакого отношения, оба генерируются отдельно. При генерации A или B известны только положение и направление.

Я искал решения, размещенные здесь:

• Quaternions, поверните модель и выровняйте по направлению
• Direct3D
  Матрица вращения от вектора и наоборот
• Вектор направления к
  Матрица вращения

Но мне не удалось успешно повернуть мою геометрию, чтобы выровнять ее вектор направления. Я чувствую, что делаю что-то довольно простое неправильно.

Любая помощь будет принята с благодарностью!