Понимание алгоритма Baeza-Yates Régnier (сопоставление нескольких строк, расширенное из Бойера-Мура)

Прежде всего, извините, если я много пишу, я попытался обобщить свои исследования, чтобы все могли понять.

R. Baeza-Yates и M. Regnier опубликовали в 1990 г. новый алгоритм поиска двумерного m.м шаблон в двумерном пн текст. Публикация очень хорошо написан и вполне понятен для новичка, как я, алгоритм описан в псевдокоде, и я смог успешно его реализовать.

Одна часть алгоритма BYR требует алгоритма Aho-Corasick. Это позволяет искать вхождения нескольких ключевых слов в тексте строки. Однако они также говорят, что эту часть их алгоритма можно значительно улучшить, используя не Aho-Corasick, а алгоритм Commentz-Walter (основанный на алгоритме Бойера-Мура, а не алгоритма Кнута-Морриса-Пратта). Они вызывают альтернативу алгоритму Commentz-Walter, альтернативу, которую они сами разработали. Это описано и объяснено в их предыдущая публикация (см. 4-ю главу).

Вот где моя проблема. Как я уже сказал, алгоритм просматривает текст и проверяет, содержит ли он слово из набора ключевых слов. Слова расположены вверх ногами и помещены в дерево. Чтобы быть эффективным, иногда необходимо пропустить несколько букв, когда он знает, что совпадений не найдено.

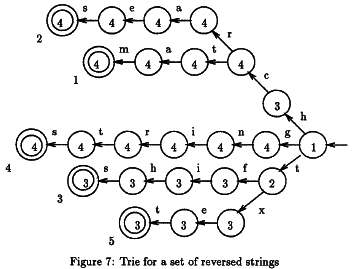
Чтобы определить количество символов, которые можно пропустить, две таблицы d а также dd должны быть рассчитаны. Тогда алгоритм очень прост:

Алгоритм работает следующим образом:

• Мы выравниваем корень дерева с позицией m в тексте и начинаем сопоставлять текст справа налево после соответствующего
  путь в три.
• Если совпадение найдено (последний узел), мы выводим индекс соответствующей строки.
• После совпадения или несовпадения мы перемещаем дерево дальше по тексту, используя максимум смещения, связанный с текущим узлом (означает dd), и
  значение d [x], где x — символ в тексте, соответствующий
  корень дерева.
• Начните сопоставлять три снова справа налево в новой позиции.

Моя проблема в том, что я не знаю, как вычислить dd функция. В своей публикации R. Baeza-Yates и M. Regnier предлагают формальное определение этого:

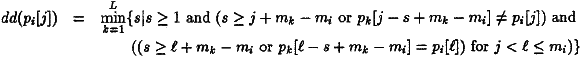
pi — это слово из набора ключевых слов, j — индекс буквы в этом слове, поэтому pi [j] похожа на узел в предыдущем примере, который я показал. Номер в узле представлен дд (узел). L — количество слов, а mi — количество букв в слове пи.

Они не дают никаких указаний относительно построения этой функции. Они только рекомендуют смотреть работа В. Риттера. Этот документ создает функцию, аналогичную ожидаемой, с той разницей, что в этом случае используется только одно ключевое слово, а не набор.

Определение dd (называемое здесь D) таково:

Можно отметить сходство с предыдущим определением, но я не все понимаю.

Псевдокод для построения этой функции приведен в статье, я реализовал ее здесь, в C ++:

int pattern[] = { 1, 2, 3, 1 };  /* I use int instead of char, simpler */
const int n = sizeof(pattern) / 4;
int D[n];
int f[n];

int j = n;
int t = n + 1;

for (int k = 1; k <= n; k++){
D[k-1] = 2 * n - k;
}

while (j > 0) {
f[j-1] = t;
while (t <= n) {
if (pattern[j-1] != pattern[t-1]) {
D[t-1] = min(D[t-1], n - j);
t = f[t-1];
}
else {
break;
}
}
t = t - 1;
j = j - 1;
}

int f1[n];
int q = t;
t = n + 1 - q;
int q1 = 1;
int j1 = 1;
int t1 = 0;while (j1 <= t) {
f1[j1 - 1] = t1;
while (t1 >= 1) {
if (pattern[j1 - 1] != pattern[t1 - 1]) {
t1 = f1[t1 - 1];
}
else {
break;
}
}
t1 = t1 + 1;
j1 = j1 + 1;
}
while (q < n) {
for (int k = q1; k <= q; k++) {
D[k - 1] = min(D[k - 1], n + q - k);
}
q1 = q + 1;
q = q + t - f1[t - 1];
t = f1[t - 1];
}

for (int i = 0; i < n; i++)
{
cout << D[i] << " ";
}

Это работает, но я не знаю, как расширить его на несколько слов, я не знаю, как совпадать с формальным определением dd дано Баеза-Йетсом и Ренье. Я сказал, что оба определения были похожи, но я не знаю, в какой степени.

Я не нашел никакой другой информации об их алгоритме, мне невозможно узнать, как реализовать построение dd, но я ищу человека, который мог бы, возможно, понять и показать мне, как туда добраться, объясняя мне связь между определениями D а также dd,