Получить точки пересечения из 2 прямоугольников

Чтобы найти пересечение, вам нужно сделать несколько простых сравнений точек:

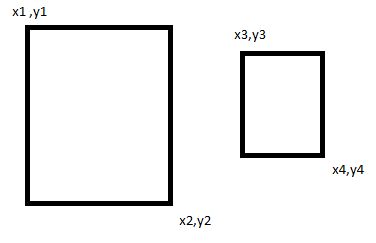
Итак, как мы можем видеть из изображения, если x3, y3 больше или равно x1, y1 и меньше или равно x2, y2, то оно находится внутри первого прямоугольника, аналогично вам нужно будет проверить, попадает ли x4, y4 внутрь диапазон от х1, у1 до х2, у2, а также.

если оба условия оказываются верными, то вы можете быть уверены, что второй прямоугольник полностью охватывается первым.

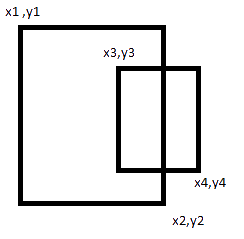
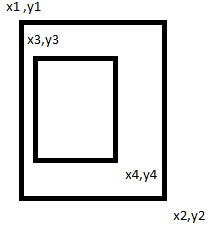
Вам нужно будет проверить и обратное, если узнаете, что внутри, что важно для вас.

Также необходимо, чтобы прямоугольники были выровнены по оси, иначе это не будет работать надежно.

Дайте мне знать, если вам нужно больше подробностей, хотя я думаю, что быстрый поиск в Google очень легко раскроет для вас более подробную информацию, но дайте мне знать, и я могу сделать учебник по столкновению с прямоугольником, если хотите.

Более подробно:

Чтобы выяснить, имеют ли прямоугольники пересечения, вы можете проверить координаты их определяющих точек, для наших целей мы будем использовать координаты верхнего левого и нижнего правого углов.
Мы можем использовать класс, чтобы сделать это проще для нас, и для максимального удобства использования кода мы можем использовать 2d Vector и 2d Point:
2dVectorPoint.h

#include <cmath>

class Vector2D
{
public:
float   x;
float   y;

Vector2D() {}
Vector2D(float inX, float inY)
{
x = inX;
y = inY;
}

Vector2D& Set(float inX, float inY)
{
x = inX;
y = inY;
return (*this);
}

float& operator [](long k)        {            return ((&x)[k]);        }

const float& operator [](long k) const        {            return ((&x)[k]);        }

Vector2D& operator +=(const Vector2D& v)
{
x += v.x;
y += v.y;
return (*this);
}

Vector2D& operator -=(const Vector2D& v)
{
x -= v.x;
y -= v.y;
return (*this);
}

Vector2D& operator *=(float t)
{
x *= t;
y *= t;
return (*this);
}

Vector2D& operator /=(float t)
{
float f = 1.0F / t;
x *= f;
y *= f;
return (*this);
}

Vector2D& operator &=(const Vector2D& v)
{
x *= v.x;
y *= v.y;
return (*this);
}

Vector2D operator -(void) const        {            return (Vector2D(-x, -y));        }

Vector2D operator +(const Vector2D& v) const        {            return (Vector2D(x + v.x, y + v.y));        }

Vector2D operator -(const Vector2D& v) const        {  return (Vector2D(x - v.x, y - v.y));        }

Vector2D operator *(float t) const        {            return (Vector2D(x * t, y * t));        }

Vector2D operator /(float t) const        {     float f = 1.0F / t; return (Vector2D(x * , y * f));        }

float operator *(const Vector2D& v) const        {            return (x * v.x + y * v.y);        }

Vector2D operator &(const Vector2D& v) const     {            return (Vector2D(x * v.x, y * v.y));        }

bool operator ==(const Vector2D& v) const        {            return ((x == v.x) && (y == v.y));        }

bool operator !=(const Vector2D& v) const        {            return ((x != v.x) || (y != v.y));        }

Vector2D& Normalize(void)                        {            return (*this /= sqrtf(x * x + y * y));        }

Vector2D& Rotate(float angle);
};class Point2D : public Vector2D
{
public:

Point2D() {}

Point2D(float r, float s) : Vector2D(r, s) {}

Point2D& operator =(const Vector2D& v)
{
x = v.x;
y = v.y;
return (*this);
}

Point2D& operator *=(float t)
{
x *= t;
y *= t;
return (*this);
}

Point2D& operator /=(float t)
{
float f = 1.0F / t;
x *= f;
y *= f;
return (*this);
}

Point2D operator -(void) const{            return (Point2D(-x, -y));        }

Point2D operator +(const Vector2D& v) const        {            return (Point2D(x + v.x, y + v.y));        }

Point2D operator -(const Vector2D& v) const        {            return (Point2D(x - v.x, y - v.y));        }

Vector2D operator -(const Point2D& p) const        {            return (Vector2D(x - p.x, y - p.y));        }

Point2D operator *(float t) const        {            return (Point2D(x * t, y * t));        }

Point2D operator /(float t) const
{
float f = 1.0F / t;
return (Point2D(x * f, y * f));
}
};inline Vector2D operator *(float t, const Vector2D& v){    return (Vector2D(t * v.x, t * v.y));}

inline Point2D operator *(float t, const Point2D& p){    return (Point2D(t * p.x, t * p.y));}

inline float Dot(const Vector2D& v1, const Vector2D& v2){    return (v1 * v2);}

inline float Magnitude(const Vector2D& v){    return (sqrtf(v.x * v.x + v.y * v.y));}

inline float InverseMag(const Vector2D& v){    return (1.0F / sqrtf(v.x * v.x + v.y * v.y));}

inline float SquaredMag(const Vector2D& v){    return (v.x * v.x + v.y * v.y);}

struct Origin2D_
{
const Point2D& operator +(const Vector2D& v)    {        return (static_cast<const Point2D&>(v));    }

Point2D operator -(const Vector2D& v)    {        return (Point2D(-v.x, -v.y));    }
};

2dVectorPoint.cpp

#include "2dVectorPoint.h"
Origin2D_ Origin2D;

Vector2D& Vector2D::Rotate(float angle)
{
float s = sinf(angle);
float c = cosf(angle);

float nx = c * x - s * y;
float ny = s * x + c * y;

x = nx;
y = ny;

return (*this);
}
extern Origin2D_ Origin2D;

Используемый код адаптирован из Вот чтобы сохранить мои пальцы.

Тогда мы можем использовать это, чтобы легко сравнить:
мы можем определить прямоугольник 1 как имеющий P1 и P2 как его границы и прямоугольник 2 как имеющий P3 и P4 как его границы, давая нам следующее сравнение:

if ( P2.y <= P3.y && P1.y >= P4.y && P2.x>= P3.x && P1.x <= P4.x )
{
return true;
}

Это вернет истинное значение для любого экземпляра пересечения или для прямоугольника 1, полностью охватывающего прямоугольник 2.

Чтобы проверить только пересечения, просто удалите проверку на равенство (возьмите все = из вышеприведенного уравнения), и вы будете проверять только на пересечения. Если у вас есть пересечение, вы можете использовать линейную алгебру для оценки точных координат.

Скажем, у блока есть радиус X и радиус Y (я знаю, что его нет, но этот термин здесь полезен).

Вы будете иметь:

rect1_x_radius = (x2-x1)/2
rect1_y_radius = (y2-y1)/2

а также

rect2_x_radius = (x4-x3)/2
rect2_y_radius = (y4-y3)/2

Теперь, если прямоугольные средние точки находятся дальше, чем сумма их радиусов в соответствующем направлении — они не сталкиваются.
В противном случае они делают — этого намека должно хватить.

Теперь вы должны быть в состоянии выполнить задание.

ОБНОВИТЬ:

Хорошо — давайте решим это для 1D — позже вы решите это для 2D. Посмотрите на этот кусок … искусства 😉

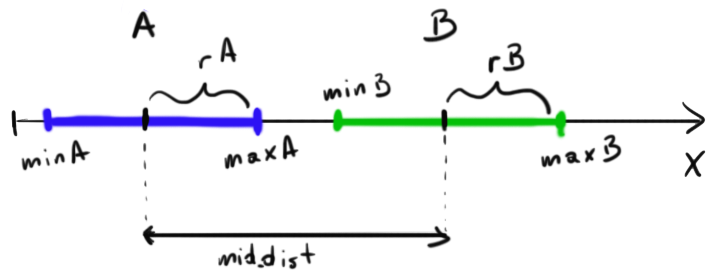
Вы видите 2 сегмента — теперь некоторые расчеты:

rA = (maxA-minA) / 2
rB = (maxB-minB) / 2

midA = minA + rA
midB = minB + rB

mid_dist = |midA - midB|

Теперь, как проверить, происходит ли столкновение? Как я уже сказал, если сумма «радиусов» меньше расстояния сегментов — столкновения нет:

if ( mid_dist > fabs(rA+rB) )
{
// no intersection
}
else
{
// segments intersect
}

Теперь ваша задача — вычислить пересечение / общую часть в 1D и 2D. Теперь все зависит от вас (вы можете прочитать ответ Андрея).

Здесь та же самая ситуация, но в 2D — две одномерные ситуации:

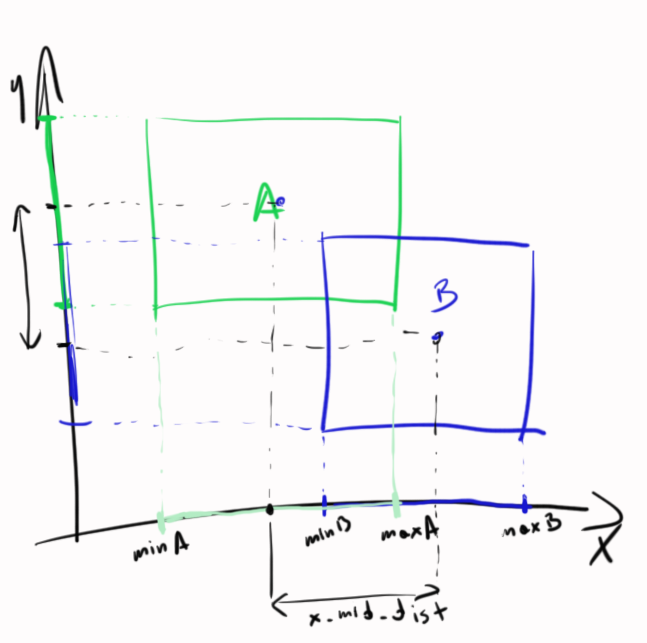
Вы можете иметь дело с x а также y Направление отдельно.

Предположим, что x1 <= x3 (первая коробка как минимум так же далеко, как и вторая). Тогда есть совпадение, если и только если x1 <= x3 <= x2,

Аналогично предположим y1 <= y3 (первая коробка, по крайней мере, так же далеко, как и вторая). Тогда есть совпадение, если и только если y1 <= y3 <= y2,

Если в обоих направлениях перекрытие, то перекрытие прямоугольника. Вы можете найти координаты, отсортировав x а также y координаты и выбрав два средних.

В псевдокоде:

if (((x1 <= x3 && x3 <= x2) || (x3 <= x1 && x1 <= x4)) // x-overlap
&&
((y1 <= y3 && y3 <= y2) || (y3 <= y1 && y1 <= y4)) // y-overlap
) {
int[] xs = {x1, x2, x3, x4};
int[] ys = {y1, y2, y3, y4};
sort(xs);
sort(ys);

// bottom-left: xs[1], ys[1]
// top-right:   xs[2], ys[2]
}