показать минимальные циклы на неориентированном графе, используя Floyd-Warshall

У меня есть некоторые проблемы с этим.
Сначала я использовал Floyd-warshall, чтобы показать все минимальные циклы на ориентированном графе, и это сработало, но затем я попытался использовать его с неориентированным графом, и оно не работает так, как мне нужно.

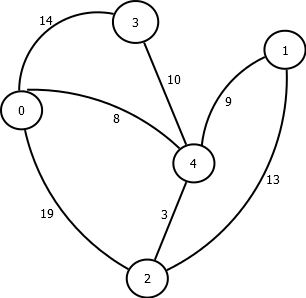
Например, допустим, у меня есть этот график:

INF     INF     19      14      8
INF     INF     13      INF     9
19      13      INF     INF     3
14      INF     INF     INF     10
8       9       3       10      INF

Это должно выглядеть примерно так:

В любом случае, поскольку вы можете представить неориентированный граф в виде ориентированного графа (точно так же, как я это делал в матрице примеров), Флойд Варшалл должен работать, но результаты оказались не такими, как я ожидал. Используя тот же пример графика, это матрица с минимальной стоимостью пути:

Минимальная стоимость пути:

16      17      11      14      8
17      18      12      19      9
11      12      6       13      3
14      19      13      20      10
8       9       3       10      6

И это матрица с путем:

 (0 4 0) (0 4 1) (0 4 2) (0 3)   (0 4)
(1 4 0) (1 4 1) (1 4 2) (1 4 3) (1 4)
(2 4 0) (2 4 1) (2 4 2) (2 4 3) (2 4)
(3 0)   (3 4 1) (3 4 2) (3 4 3) (3 4)
(4 0)   (4 1)   (4 2)   (4 3)   (4 2 4)

Поскольку меня интересуют только циклы, мне нужна только диагональ матрицы.

В любом случае, давайте возьмем 0 -> 0: результат (0 4 0), стоимость которого равна 16

Так или иначе, так как я ищу минимальные циклы, я ожидал что-то вроде:

0 -> 0, Path (0 4 2 0) (или 0 2 4 0, поскольку это неориентированный граф, но мне нужен только один из них) и стоимость 30.

На самом деле это код floyd-warshall:

for (k = 0; k < V; k++)
{
for (i = 0; i < V; i++)
{
for (j = 0; j < V; j++)
{
if (dist[i][k] != INF && dist[k][j] != INF &&
dist[i][k] + dist[k][j] < dist[i][j]) {

dist[j][i] = dist[i][j] = dist[i][k] + dist[k][j];
path[i][j] = path[j][i] = path[k][j];
}
}
}
}

Я действительно не знаю, что мне нужно изменить, чтобы получить правильный результат (или, может быть, это правильный результат, и я думаю, что нет).