поиск пути — Применение алгоритма поиска пути (Tower Defense) в переполнении стека

Я не знаю точных внутренних элементов вашего алгоритма, но вы можете легко получить кратчайший путь к месту назначения, сопоставив каждому узлу минимальное расстояние от начального узла, найденного для текущего запроса пути.

Таким образом, всякий раз, когда вы находите другой путь, который проходит из той же ячейки, если расстояние меньше сохраненного, тогда этот путь лучше предыдущего, в противном случае вы можете проигнорировать его и перейти к следующему.

Таким образом, вы можете получить более одного пути, который достигает цели, но все они имеют одинаковую длину (таким образом, вы можете просто выбрать один из них). Достигнув узла цели, вы можете вернуться назад: для каждого узла на расстоянии Икс начиная с цели поиска соседа на расстоянии х-1.

Просто чтобы дать вам графическое представление о том, что я имею в виду:

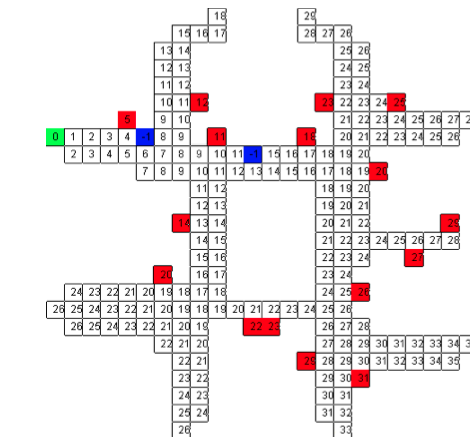
Имейте в виду, что это не самое быстрое решение, и оно подойдет только для небольших мозаичных карт, для более крупных вам потребуются более качественные алгоритмы, чем поиск в ширину.

Выполните поиск в глубину (dfs) по окончательной сетке, которую вы получите.

http://en.wikipedia.org/wiki/Depth-first_search

Вы получите индивидуальные пути. Если вы хотите выбрать самый короткий, есть несколько вариантов оптимизации, которые вы можете сделать.

• Сохраняйте максимальный лимит, если dfs смотрит дальше, пропустите этот путь.
• Если вы найдете путь длиной меньше максимального предела. Установите максимальный предел для этого.

Надеюсь, это поможет.

РЕДАКТИРОВАТЬ: Я написал этот код, и он должен работать для вас. Это даст кратчайший путь, в векторе< pair> как координаты x, y.

#include <iostream>
#include <fstream>
#include <vector>
#include <cstring>

using namespace std;

ifstream fin("map.txt");

int width, height;
int map[10][10];
// Start (x,y), End (x,y)
int sy, sx, ey, ex;

bool visited[10][10];

vector<pair<int, int> > final_path;
int max_size = 9999;

void getInput() {
fin >> width >>  height;

for (int i = 0; i < height; i++) {
for (int j = 0; j < width; j++) {
int x;
fin >> x;
map[i][j] = x;

if(x == 8){
sy = i;
sx = j;
}

if(x == 9){
ey = i;
ex = j;
}
}
}
}

void dfs(int x, int y, vector<pair<int, int> > path) {
if(path.size() > max_size){
cout << "Returning : path size too big" << endl;
return;
}

if(x < 0 || x >= width || y < 0 || y >= height){
cout << "Returning : bounds" << endl;
return;
}

// If the tile is blocked, can't go there
if(map[y][x] == 0){
cout << "Returning : blocked" << endl;
return;
}

if(visited[y][x]){
cout << "Returning : visited" << endl;
return;
}

// We don't want to revisit a tile
visited[y][x] = true;

cout << "Visiting " << x << " " << y << endl;

path.push_back(make_pair(x, y));
if(map[y][x] == 9) {
final_path = path;
visited[y][x] = false;
return;
}

dfs(x, y - 1, path);
dfs(x + 1, y, path);
dfs(x, y + 1, path);
dfs(x - 1, y, path);

visited[y][x] = false;

return;
}

int main() {

getInput();
cout << "Got Input" << endl;
cout << width << " " << height << endl;

memset(visited, 0, sizeof(visited));
vector<pair<int, int> > starting_path;

cout << sx << " " << sy << endl;

dfs(sx, sy, starting_path);

cout << "Path size is " << final_path.size() << endl;

for(int i = 0; i < final_path.size(); i++){
cout << final_path[i].first << " " << final_path[i].second << endl;
}

return 0;
}

map.txt содержит карту, которую вы дали в вопросе.