подсчитать количество смежных прямоугольников

Question

подсчитать количество смежных прямоугольников

Мой код печатает наборы (X, Y) координат в 2D-пространстве в диапазоне [0,1].

void Rect_Print() {
cout << "In counter-clockwise fashion" << endl;
cout << "#Rectangle    (   x0,   y0)   (   x1,   y1) " << endl;

for (int b=0; b<Rect_Count; b++) {
double Area = (Rect[b].x0 - Rect[b].x1) * (Rect[b].y0 - Rect[b].y1);

cout << fixed << setprecision(4) << (b+1) <<
"  (" << Rect[b].x0 << "," << Rect[b].y0 <<
")   (" << Rect[b].x1 << "," << Rect[b].y1 << ")" << endl;
}

cout << "Number of divisions (N = 3j-2) = " << Rect_Count << endl;
}

Эти точки делят единичный квадрат на (3j-2) под прямоугольники (не равномерно). Для каждого конкретного прямоугольника я бы хотел подсчитать общее количество прямоугольников, прилегающих к нему.

пример

Предположим, что первая координата делит единичный квадрат на четыре прямоугольника, например:

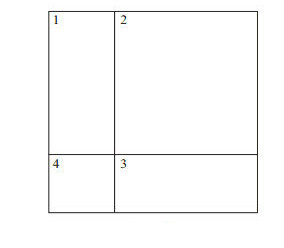
На этой картинке вы можете увидеть, есть три прямоугольника смежный с прямоугольником-3.
Если я продолжу в том же духе, то после шестого шага единичный квадрат разделим на 19 прямоугольников. Так это выглядит так:

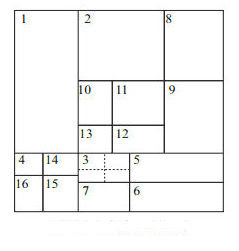
Сейчас есть пять прямоугольников рядом с прямоугольником-3. шесть прямоугольников рядом с прямоугольником-11.

Предположим, у меня есть наборы десять тысяч координаты, и они подразделяют квадрат на маленькие под прямоугольники. Я хотел бы использовать c ++ для подсчета количества прямоугольников, смежных с каждым из них. Как мне это сделать?

После поиска в Интернете кажется, что Фланн может помочь мне в этом. Я прочитал руководство пользователя, но не мог понять, как я могу это сделать.

Может кто-нибудь мне помочь?

1

algorithm c++nearest-neighbor rectangles

Решение

Другие решения

Вы можете искать R-дерево или KD-дерево. Алгоритм древовидной карты работает аналогично. Хорошее начало — это отсортировать блоки и поместить их в дерево, рекурсивно разделив их по оси 2 и посмотреть, куда помещается следующий блок.

0

Источник

Accepted Answer

Я хотел бы предложить вам структурировать это с помощью чего-то похожего четырехугольного дерева (см. Wikipedia Quadtree статья). Разница здесь в том, что вы не делите равномерно подузлы дерева четырехугольников — вы разделяете в вставленных точках.

Затем вы можете пройтись по дереву в поисках пересекающихся ребер.

Если у узла нет ребра, которое пересекает ваш прямоугольник запроса, вам не нужно повторять его дочерние элементы, что сэкономит процессорное время при выполнении этого для 10 000 прямоугольников, поскольку сложность будет логарифмической, а не линейной.

Листовые листы дерева — это ваш список прямоугольников, поэтому вы должны считать только те прямоугольники, которые являются листьями дерева и пересекаются с прямоугольником запроса.

Это также удобный способ обработки разбиения прямоугольников — когда вы вставляете точку, вы можете вернуться в дерево, чтобы найти прямоугольник для быстрого разделения.

0