Почему развертывание цикла не влияет на большой набор данных?

Я хотел сравнить разницу в скорости выполнения между развернутым циклом и циклом for, примененным к triangle объект. Весь пример доступен Вот.

Вот полный код:

#include <iostream>
#include <vector>
#include <array>
#include <random>
#include <functional>
#include <chrono>
#include <fstream>

template<typename RT>
class Point
{
std::array<RT,3> data;

public:

Point() = default;

Point(std::initializer_list<RT>& ilist)
:
data(ilist)
{}

Point(RT x, RT y, RT z)
:
data({x,y,z})
{};

RT& operator[](int i)
{
return data[i];
}

RT operator[](int i) const
{
return data[i];
}

const Point& operator += (Point const& other)
{
data[0] += other.data[0];
data[1] += other.data[1];
data[2] += other.data[2];

return *this;
}

const Point& operator /= (RT const& s)
{
data[0] /= s;
data[1] /= s;
data[2] /= s;

return *this;
}

};

template<typename RT>
Point<RT> operator-(const Point<RT>& p1, const Point<RT>& p2)
{
return Point<RT>(p1[0] - p2[0], p1[1] - p2[1], p1[2] - p2[2]);
}

template<typename RT>
std::ostream& operator<<(std::ostream& os , Point<RT> const& p)
{
os << p[0] << " " << p[1] << " " << p[2];
return os;
}

template<typename Point>
class Triangle
{
std::array<Point, 3> points;

public:

typedef typename std::array<Point, 3>::value_type value_type;

typedef Point PointType;

Triangle() = default;

Triangle(std::initializer_list<Point>& ilist)
:
points(ilist)
{}

Triangle(Point const& p1, Point const& p2, Point const& p3)
:
points({p1, p2, p3})
{}

Point& operator[](int i)
{
return points[i];
}

Point operator[](int i) const
{
return points[i];
}

auto begin()
{
return points.begin();
}

const auto begin() const
{
return points.begin();
}

auto end()
{
return points.end();
}

const auto end() const
{
return points.end();
}
};

template<typename Triangle>
typename Triangle::PointType barycenter_for(Triangle const& triangle)
{
typename Triangle::value_type barycenter;

for (const auto& point : triangle)
{
barycenter += point;
}

barycenter /= 3.;

return barycenter;
}

template<typename Triangle>
typename Triangle::PointType barycenter_unrolled(Triangle const& triangle)
{
typename Triangle::PointType barycenter;

barycenter += triangle[0];
barycenter += triangle[1];
barycenter += triangle[2];

barycenter /= 3.;

return barycenter;
}

template<typename TriangleSequence>
typename TriangleSequence::value_type::value_type
barycenter(
TriangleSequence const& triangles,
std::function
<
typename TriangleSequence::value_type::value_type (
typename TriangleSequence::value_type const &
)
> triangle_barycenter
)
{
typename TriangleSequence::value_type::value_type barycenter;

for(const auto& triangle : triangles)
{
barycenter += triangle_barycenter(triangle);
}

barycenter /= double(triangles.size());

return barycenter;
}

using namespace std;

int main(int argc, const char *argv[])
{
typedef Point<double> point;
typedef Triangle<point> triangle;

const int EXP = (atoi(argv[1]));

ofstream outFile;
outFile.open("results.dat",std::ios_base::app);

const unsigned int MAX_TRIANGLES = pow(10, EXP);

typedef std::vector<triangle> triangleVector;

triangleVector triangles;

std::random_device rd;
std::default_random_engine e(rd());
std::uniform_real_distribution<double> dist(-10,10);

for (unsigned int i = 0; i < MAX_TRIANGLES; ++i)
{
triangles.push_back(
triangle(
point(dist(e), dist(e), dist(e)),
point(dist(e), dist(e), dist(e)),
point(dist(e), dist(e), dist(e))
)
);
}

typedef std::chrono::high_resolution_clock Clock;

auto start = Clock::now();
auto trianglesBarycenter = barycenter(triangles, [](const triangle& tri){return barycenter_for(tri);});
auto end = Clock::now();

auto forLoop = end - start;

start = Clock::now();
auto trianglesBarycenterUnrolled = barycenter(triangles, [](const triangle& tri){return barycenter_unrolled(tri);});
end = Clock::now();

auto unrolledLoop = end - start;

cout << "Barycenter difference (should be a zero vector): " << trianglesBarycenter - trianglesBarycenterUnrolled << endl;

outFile << MAX_TRIANGLES << " " << forLoop.count() << " " << unrolledLoop.count() << "\n";

outFile.close();

return 0;
}

Пример состоит из типа Point и типа Triangle. Сравнительный расчет — это расчет барицентра треугольника. Это можно сделать с помощью цикла for:

for (const auto& point : triangle)
{
barycenter += point;
}

barycenter /= 3.;

return barycenter;

или его можно развернуть, поскольку треугольник имеет три точки:

barycenter += triangle[0];
barycenter += triangle[1];
barycenter += triangle[2];

barycenter /= 3.;

return barycenter;

Поэтому я хотел проверить, какая функция, которая вычисляет барицентр, будет быстрее для набора треугольников. Чтобы максимально использовать возможности теста, я сделал количество треугольников, оперируемых с переменной, выполнив основную программу с целочисленным аргументом экспоненты:

./main 6

в результате чего 10 ^ 6 треугольников. Количество треугольников колеблется от 100 до 1e06. Основная программа создает файл «results.dat». Чтобы проанализировать результаты, я написал небольшой скрипт на python:

#!/usr/bin/python

from matplotlib import pyplot as plt
import numpy as np
import os

results = np.loadtxt("results.dat")

fig = plt.figure()

ax1 = fig.add_subplot(111)
ax2 = ax1.twinx()

ax1.loglog();
ax2.loglog();

ratio = results[:,1] / results[:,2]

print("Speedup factors unrolled loop / for loop: ")
print(ratio)

l1 = ax1.plot(results[:,0], results[:,1], label="for loop", color='red')
l2 = ax1.plot(results[:,0], results[:,2], label="unrolled loop", color='black')
l3 = ax2.plot(results[:,0], ratio, label="speedup ratio", color='green')

lines  = [l1, l2, l3];

ax1.set_ylabel("CPU count")
ax2.set_ylabel("relative speedup: unrolled loop / for loop")

ax1.legend(loc="center right")
ax2.legend(loc="center left")

plt.savefig("results.png")

И чтобы использовать все это на вашем компьютере, скопируйте пример кода и скомпилируйте его:

g++ -std=c++1y -O3 -Wall -pedantic -pthread main.cpp -o main

Чтобы отобразить измеренное время ЦП для различных функций барицентра, запустите скрипт python (я назвал его plotResults.py):

 for i in {1..6}; do ./main $i; done
./plotResults.py

Я ожидал увидеть, что относительное ускорение между развернутым циклом и for цикл (для времени цикла / развернутого цикла) будет увеличиваться с размером установленного треугольника. Этот вывод вытекает из логики: если развернутый цикл быстрее, чем цикл for, выполнение большого количества развернутых циклов должно выполняться быстрее, чем выполнение большого числа циклов for. Вот диаграмма результатов, которые генерирует вышеприведенный скрипт python:

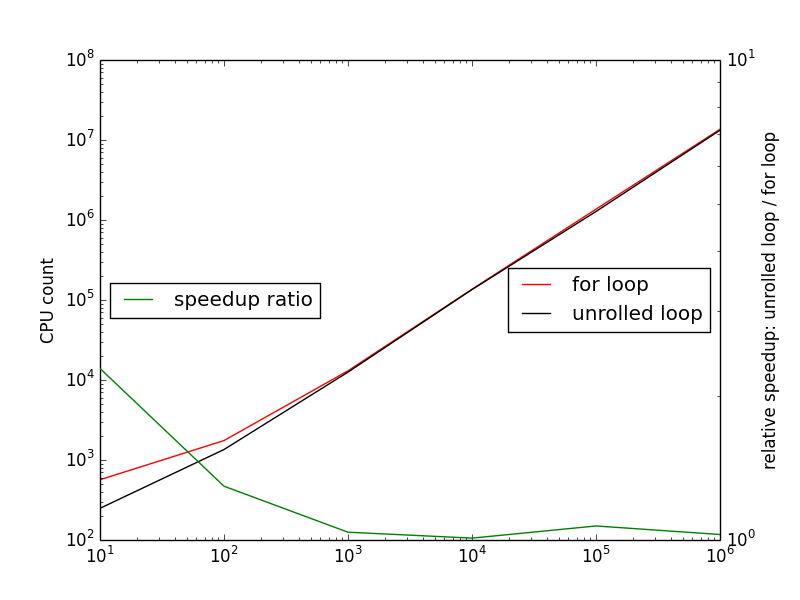
Влияние циклического развертывания умирает быстро. Как только я работаю с более чем 100 треугольниками, кажется, нет никакой разницы. Посмотрим на ускорение, рассчитанное скриптом Python:

[ 3.13502399  2.40828402  1.15045831  1.0197221   1.1042312   1.26175165
0.99736715]

ускорение при использовании 100 треугольников (3-е место в списке соответствует 10 ^ 2) составляет 1,15.

Я пришел сюда, чтобы узнать, что я сделал не так, потому что здесь должно быть что-то не так, ИМХО. 🙂 Заранее спасибо.

редактировать: построение коэффициентов промахов кэша

Если программа запускается так:

for input in {2..6}; do valgrind --tool=cachegrind  ./main $input; done

cachegrind генерирует кучу выходных файлов, которые могут быть проанализированы с grep за PROGRAM TOTALSсписок чисел, представляющих следующие данные, взятые из кашгринд руководство:

Cachegrind собирает следующую статистику (сокращения, используемые для
каждая статистика указана в скобках):

I cache reads (Ir, which equals the number of instructions executed), I1 cache read misses (I1mr) and LL cache instruction read

промахов (ILmr).

D cache reads (Dr, which equals the number of memory reads), D1 cache read misses (D1mr), and LL cache data read misses (DLmr).

D cache writes (Dw, which equals the number of memory writes), D1 cache write misses (D1mw), and LL cache data write misses (DLmw).

Conditional branches executed (Bc) and conditional branches mispredicted (Bcm).

Indirect branches executed (Bi) and indirect branches mispredicted (Bim).

И «комбинированный» коэффициент пропуска кэша определяется как: (ILmr + DLmr + DLmw) / (Ir + Dr + Dw)

Выходные файлы могут быть проанализированы следующим образом:

for file in cache*; do cg_annotate $file | grep TOTALS >> program-totals.dat; done
sed -i 's/PROGRAM TOTALS//'g program-totals.dat

и результирующие данные могут быть затем визуализированы с помощью этого сценария Python:

#!/usr/bin/python
from matplotlib import pyplot as plt
import numpy as np
import os
import locale

totalInput = [totalInput.strip().split(' ') for totalInput in open('program-totals.dat','r')]

locale.setlocale(locale.LC_ALL, 'en_US.UTF-8' )

totals = []

for line in totalInput:
totals.append([locale.atoi(item) for item in line])

totals = np.array(totals)

# Assumed default output format
# Ir I1mr  ILmr Dr Dmr DLmr Dw D1mw DLmw
# 0   1     2   3   4   5   6   7    8
cacheMissRatios = (totals[:,2] + totals[:,5] + totals[:,8]) / (totals[:,0] + totals[:,3] + totals[:,6])

fig = plt.figure()
ax1 = fig.add_subplot(111)
ax1.loglog()

results = np.loadtxt("results.dat")
l1 = ax1.plot(results[:,0], cacheMissRatios, label="Cachegrind combined cache miss ratio", color='black', marker='x')
l1 = ax1.plot(results[:,0], results[:,1] / results[:,2], label="Execution speedup", color='blue', marker='o')

ax1.set_ylabel("Cachegrind combined cache miss ratio")
ax1.set_xlabel("Number of triangles")
ax1.legend(loc="center left")

plt.savefig("cacheMisses.png")

Таким образом, построение диаграммы комбинированного коэффициента несоответствия LL и ускорения программы при развертывании треугольного цикла доступа приводит к следующей диаграмме:

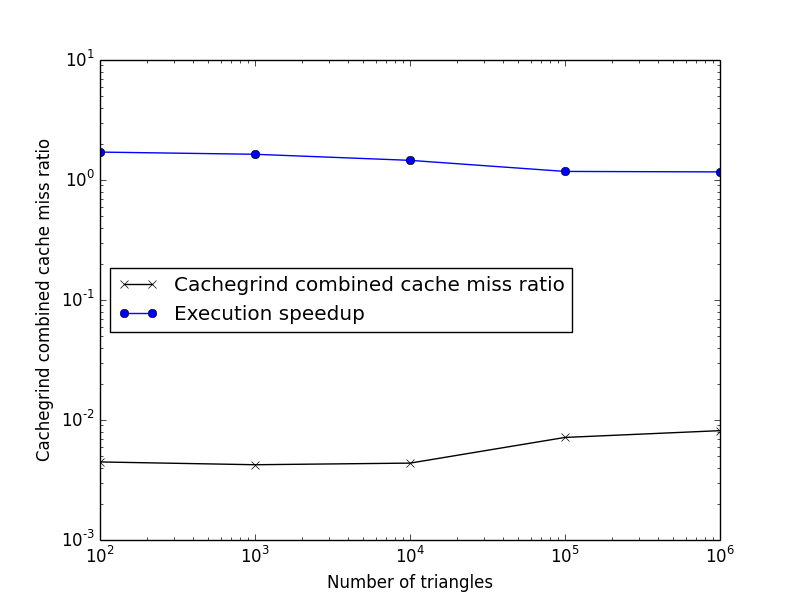
И, похоже, существует зависимость в уровне ошибок LL: при повышении скорости замедление программы снижается. Но все же я не вижу четкой причины узкого места.

Правильно ли анализировать совокупный коэффициент пропусков LL? Если посмотреть на выходной сигнал valgrind, сообщается, что все показатели промахов составляют менее 5%, это должно быть вполне нормально, верно?